2. Differentialrechnung
  3. Anwendungen
  4. Kurvendiskussion

7.5.1 Kurvendiskussion



Gegeben ist eine differenzierbare Funktion f: ]a;b[ →ℝ mit Abbildungsvorschrift x→y=f(x) für x∈ ]a;b[ . Eine vollständige Kurvendiskussion für f besteht in diesem Kurs aus folgenden Angaben:

  • Maximaler Definitionsbereich

  • Achsenschnittpunkte des Graphen

  • Symmetrie des Graphen

  • Grenzverhalten/Asymptoten

  • Die ersten Ableitungen

  • Extremwerte

  • Monotonieverhalten

  • Wendestellen

  • Krümmungsverhalten

  • Skizze des Graphen



Viele dieser Punkte wurden bereits in Modul 6 behandelt. Daher wiederholt das Folgende nur kurz, was unter den einzelnen Schritten der Kurvendiskussion zu verstehen ist. Im Anschluss wird eine Kurvendiskussion detailliert an einem Beispiel durchgesprochen.

Der erste Teil der Kurvendiskussion besteht aus algebraischen und geometrischen Aspekten von f:

Maximaler Definitionsbereich
Es werden alle reellen Zahlen x bestimmt, für die f(x) existiert. Die Menge D all dieser Zahlen wird maximaler Definitionsbereich genannt.
Schnittpunkte mit den Achsen
 
  • x-Achse: Alle Nullstellen von f werden bestimmt.

  • y-Achse: Der Funktionswert f(0) (falls 0∈D) wird berechnet.

Symmetrie des Graphen
Der Graph der Funktion ist symmetrisch zur y-Achse, wenn f(-x)=f(x) für alle x∈D ist. Dann heißt die Funktion f auch gerade. Ist f(-x)=-f(x) für alle x∈D, so ist der Graph zum Ursprung (0;0) des Koordinatensystems punktsymmetrisch. In diesem Falle nennt man die Funktion f auch ungerade.
Asymptotisches Verhalten an den Rändern des Definitionsbereichs
Die Grenzwerte der Funktion f an den Grenzen ihres Definitionsbereichs werden untersucht.


Im zweiten Teil wird die Funktion mittels Folgerungen aus der Ableitung analytisch untersucht. Dazu müssen natürlich zunächst die erste und die zweite Ableitung berechnet werden, sofern diese existieren.

Ableitungen
Berechnung der ersten und zweiten Ableitung (soweit vorhanden).
Extremwerte und Monotonie
Notwendige Bedingung für Extremstellen x (sofern x∈D kein Randpunkt von D ist): f'(x)=0

Wir berechnen also diejenigen Stellen x0 , an denen die Ableitung f' den Wert Null annimmt. Wenn an diesen Stellen auch die zweite Ableitung f'' existiert, gilt:
  • f''( x0 )>0: x0 ist eine Minimalstelle von f.

  • f''( x0 )<0: x0 ist eine Maximalstelle von f.

Die Funktion f ist auf denjenigen Intervallen des Definitionsbereichs monoton wachsend, auf denen f'(x)≥0 gilt. Sie ist dort monoton fallend, wo f'(x)≤0 ist.
Wendestellen und Krümmungseigenschaften
Notwendige Bedingung für Wendestellen (sofern die zweite Ableitung f'' existiert): f''(x)=0

Wenn f''( w0 )=0 und f(3) ( w0 )≠0 ist, dann ist w0 eine Wendestelle, d.h. f ändert an dieser Stelle das Krümmungsverhalten.

Die Funktion f ist auf denjenigen Intervallen des Definitionsbereichs konvex (linksgekrümmt), auf denen f(2) (x)≥0 gilt. Sie ist konkav (rechtsgekrümmt) dort, wo f(2) (x)≤0 ist.
Skizze des Graphen
Eine Skizze des Graphen in einem geeigneten Koordinatensystem wird angefertigt, und zwar unter Berücksichtigung der während der Kurvendiskussion gewonnenen Daten.


Ausführliches Beispiel

Es soll eine Funktion f mit dem Funktionsterm

f(x)  =   4x x2 +2

untersucht werden.

Maximaler Definitionsbereich
Der maximale Definitionsbereich dieser Funktion ist Df =ℝ, da der Nenner der Funktion x2 +2≥2 ist, also niemals Null wird, und daher keine Stellen ausgeschlossen werden müssen.  
 
Achsenschnittpunkte
Die Nullstellen der Funktion entsprechen den Nullstellen des Zählers. Daher schneidet der Graph von f die x-Achse nur im Nullpunkt (0;0), denn der Zähler wird nur für x=0 zu Null. Dies ist auch der einzige Schnittpunkt mit der y-Achse, da f(0)=0 ist.  
 
Symmetrie
Um das Symmetrieverhalten zu untersuchen, wird das Argument x durch (-x) ersetzt. Es gilt

f(-x)  =   4·(-x) (-x )2 +2   =  - 4x x2 +2   =  -f(x)

für alle x∈ℝ. Der Graph von f ist folglich punktsymmetrisch zum Ursprung.  
 
Grenzverhalten
Die Funktion ist auf ganz ℝ definiert, daher ist nur das Grenzverhalten für x→∞ und x→-∞ zu untersuchen. Da f(x) ein Bruch aus zwei Polynomen ist und der Nenner die höhere Potenz besitzt, ist die x-Achse die waagerechte Asymptote in beide Richtungen:

limx→±∞ f(x)=0 .

 
 
Ableitungen
Die ersten beiden Ableitungen der Funktion folgen mit Hilfe der Quotientenregel:

f'(x)  =  4· 1·( x2 +2)-x·2x ( x2 +2 )2   =  4· - x2 +2 ( x2 +2 )2  .

Erneutes Ableiten und Vereinfachen ergibt

f''(x) = 4· -2x( x2 +2 )2 -(- x2 +2)·2( x2 +2)·2x ( x2 +2 )4 = 4· -2x( x2 +2)-(- x2 +2)·4x ( x2 +2 )3 = 4· -2 x3 -4x+4 x3 -8x ( x2 +2 )3 = 4· 2 x3 -12x ( x2 +2 )3 = 8· x( x2 -6) ( x2 +2 )3  .

 
Extremwerte
Die notwendige Bedingung für eine Extremstelle, f'(x)=0, ist hier gleichbedeutend mit - x2 +2=0. Man erhält also x1 =2 und x2 =-2. Es muss noch das Verhalten der zweiten Ableitung an diesen Stellen untersucht werden:

f''( x1 )  =  8 2·(2-6) (2+2 )3 <0 ,   f''( x2 )  =  8 (-2)·(2-6) (2+2 )3 >0 .

Folglich ist x1 eine Maximalstelle und x2 eine Minimalstelle von f. Durch Einsetzen in f resultieren das Maximum (2;2) und das Minimum (-2;-2) von f.  
 
Monotonieverhalten
Da f auf ganz ℝ definiert ist, kann das Monotonieverhalten aus der Lage der Extremstellen und aus deren Typ abgelesen werden: f ist monoton fallend auf ]-∞;-2[ , monoton wachsend auf ]-2;2[ und monoton fallend auf ]2;∞[ . Monotonieintervalle werden stets in offener Form angegeben.  
 
Wendestellen
Aus der notwendigen Bedingung für Wendestellen f''(x)=0 erhält man die Gleichung 8x( x2 -6)=0. Somit sind w0 =0, w1 =6 und w2 =-6 die einzigen Lösungen. Das Polynom im Nenner von f'' ist stets größer als Null. Da das Zählerpolynom nur einfache Nullstellen besitzt, ändert f''(x) in allen diesen Stellen das Vorzeichen. Es handelt sich daher um Wendestellen von f. Die Wendepunkte (0;0), (6; 1 2 6), (-6;- 1 2 6) ergeben sich durch Einsetzen der Wendestellen in f.  
 
Krümmungsverhalten
Die zweimal differenzierbare Funktion f ist konvex, wenn die zweite Ableitung größer oder gleich Null ist. Sie ist konkav, wenn die zweite Ableitung kleiner oder gleich Null ist. Da das Polynom im Nenner von f''(x) stets positiv ist, genügt es, das Vorzeichen des Polynoms p(x)=8x(x-6)(x+6) im Zähler zu untersuchen. Für 0<x<6 ist es negativ (dort ist f konkav). Für x>6 ist es positiv (dort ist f konvex). Da f punktsymmetrisch ist, folgt, dass f auf den Intervallen ]-6;0[ und ]6;∞[ konvex sowie auf ]-∞;-6[ und ]0;6[ konkav ist.  
 
Skizze des Graphen
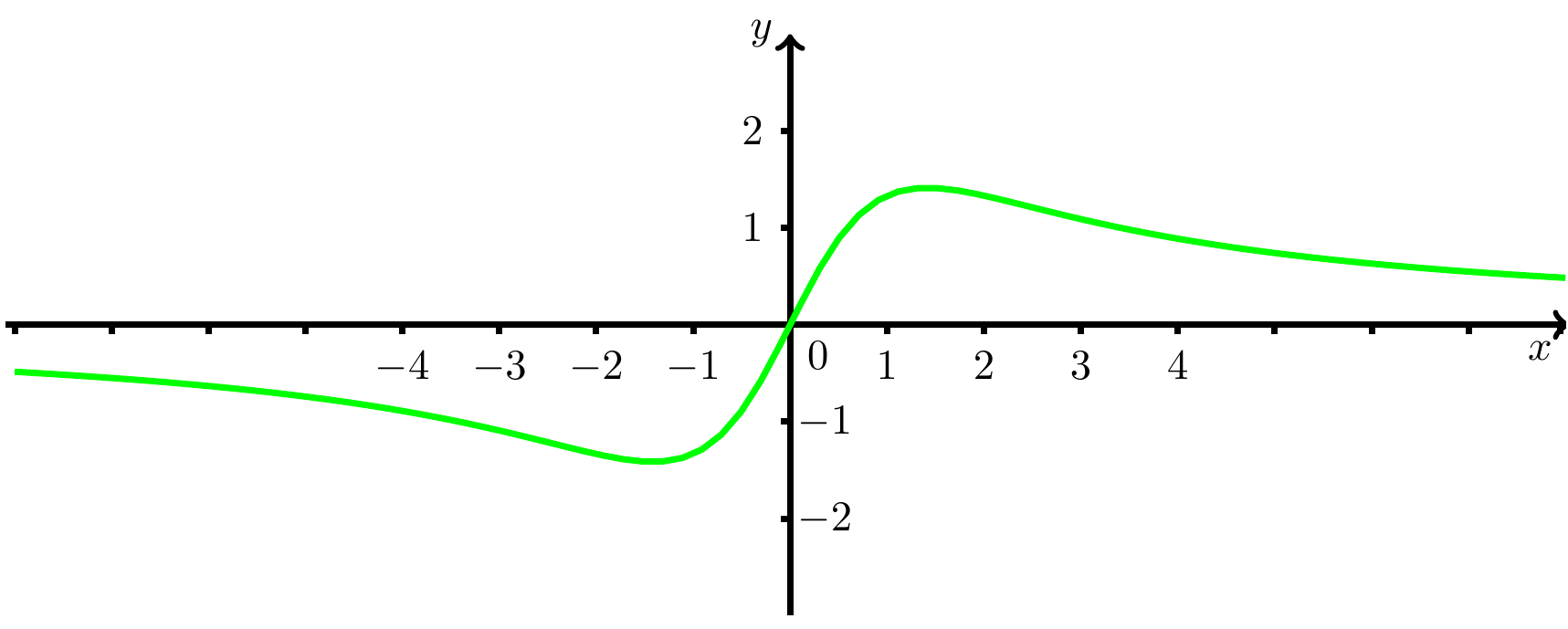
./BildKurvendiskussion1.png
Abbildung 7.5.1: Der Graph der Funktion f, skizziert auf dem Intervall [-8;8].