Onlinebrückenkurs Mathematik Abschnitt 2.1.5 Auflösen quadratischer Gleichungen

Kapitel 2 Gleichungen in einer Unbekannten - Abschnitt 2.1 Einfache Gleichungen

2.1.5 Auflösen quadratischer Gleichungen

Info 2.1.20

Eine quadratische Gleichung ist eine Gleichung der Form

a x^{2} + b x + c = 0

mit

a \neq 0

, oder

x^{2} + p x + q = 0

in normierter Form. Diese erhält man durch Division der gesamten Gleichung durch

a

.

Für eine quadratische Gleichung in einer Unbestimmten (hier

x

) gibt es nur drei Möglichkeiten:

Sie ist nicht lösbar: $L = {}$ ,
sie besitzt eine einzige Lösung $L = {x_{1}}$ ,
sie besitzt zwei verschiedene Lösungen $L = {x_{1}; x_{2}}$ .

Die Lösungen erhält man dabei über quadratische Lösungsformeln.

Info 2.1.21

Die $p q$ -Formel für die Gleichung

x^{2} + p x + q = 0

lautet

x_{1,2} = - \frac{p}{2} \pm \sqrt{\frac{1}{4} p^{2} - q} .

Dabei besitzt die Gleichung

keine (reelle) Lösung, falls $\frac{1}{4} p^{2} - q < 0$ ist (dann darf man die Wurzel nicht ziehen),
eine einzige Lösung $x_{1} = - \frac{p}{2}$ , falls $\frac{1}{4} p^{2} = q$ ist und die Wurzel verschwindet,
zwei verschiedene Lösungen, falls die Wurzel eine positive Zahl ist.

Der hierbei betrachtete Ausdruck unter der Wurzel,

D : = \frac{1}{4} p^{2} - q

, heißt Diskriminante.

Die Lösung einer quadratischen Gleichung wird häufig durch eine alternative Formel beschrieben:

Info 2.1.22

Für die Gleichung

a x^{2} + b x + c = 0

mit

a \neq 0

lautet die $a b c$ -Formel oder Mitternachtsformel

x_{1,2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} .

Dabei besitzt die Gleichung

keine (reelle) Lösung, falls $b^{2} - 4 a c < 0$ ist (eine Quadratwurzel negativer Zahlen existiert im Reellen nicht),
eine einzige Lösung $x_{1} = - \frac{b}{2 a}$ , falls $b^{2} = 4 a c$ ist und die Wurzel verschwindet,
zwei verschiedene Lösungen, falls die Wurzel eine positive Zahl ist.

Auch der hierbei betrachtete Ausdruck unter der Wurzel,

D : = b^{2} - 4 a c

, heißt Diskriminante.

Beide Formeln führen natürlich auf dieselben Lösungen. (Für die Anwendung der

p q

-Formel ist die Gleichung durch den Vorfaktor

a

des quadratischen Terms zu dividieren.)

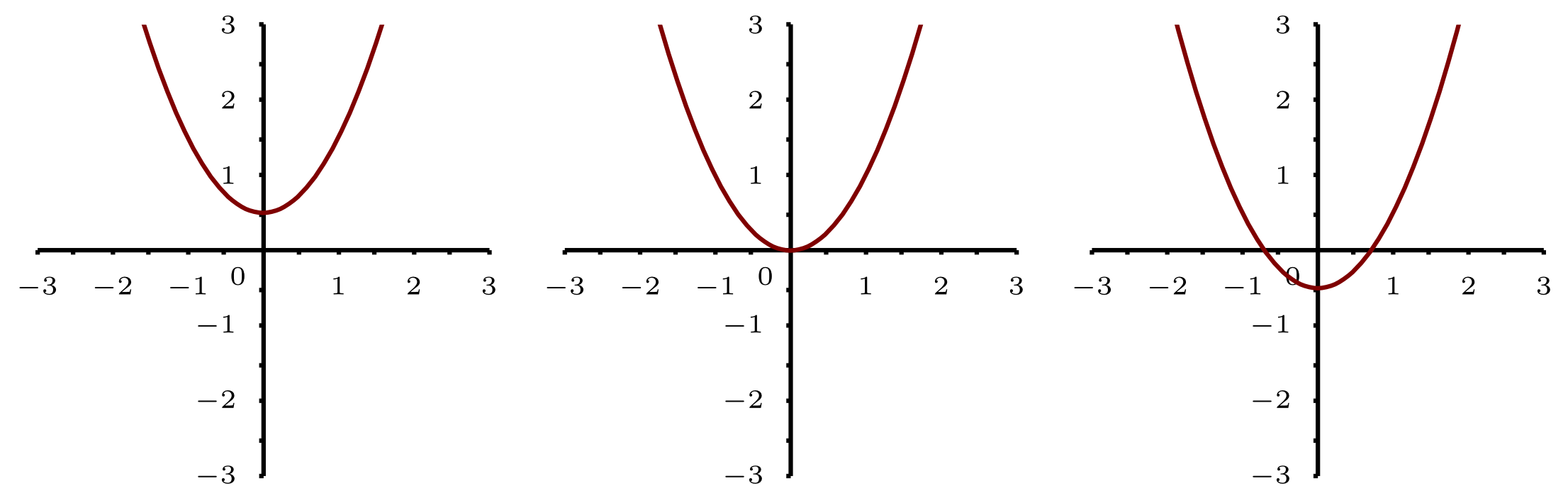
Die drei unterschiedenen Situationen entsprechen den drei möglichen Schnitten, die der Graph einer (für der Fall der

p q

-Formel) nach oben geöffneten Parabel der Form

f (x) = x^{2} + p x + q

mit der

x

-Achse haben kann:

Die drei Situationen: Kein Schnittpunkt, ein Schnittpunkt und zwei Schnittpunkte mit der

x

-Achse.

Beispiel 2.1.23
Die quadratische Gleichung

x^{2} - x + 1 = 0

hat keine Lösung, denn in der

p q

-Formel ist

\frac{1}{4} p^{2} - q = - \frac{3}{4}

negativ. Dagegen besitzt

x^{2} - x - 1 = 0

die beiden Lösungen

\begin{matrix} x_{1} & = & \frac{1}{2} + \sqrt{\frac{1}{4} + 1} = \frac{1}{2} (1 + \sqrt{5}), \\ x_{2} & = & \frac{1}{2} - \sqrt{\frac{1}{4} + 1} = \frac{1}{2} (1 - \sqrt{5}) . \end{matrix}

Info 2.1.24

Der Funktionsausdruck einer Parabel liegt in Scheitelpunktform vor, wenn er die Form

f (x) = a \cdot (x - s)^{2} - d

mit

a \neq 0

besitzt. In dieser Situation ist

(s; - d)

der Scheitelpunkt der Parabel. Die zugehörige quadratische Gleichung für

f (x) = 0

lautet dann

a \cdot (x - s)^{2} = d

.

Dividiert man diese Gleichung durch

a

, dann erhält man die äquivalente quadratische Gleichung

(x - s)^{2} = \frac{d}{a}

. Da die linke Seite ein Quadrat eines reellen Ausdrucks ist, existieren nur Lösungen, wenn auch die rechte Seite nicht negativ ist, d.h.

\frac{d}{a} \geq 0

gilt. Durch Wurzelziehen unter Beachtung beider möglicher Vorzeichen folgt dann

x - s = \pm \sqrt{\frac{d}{a}}

.

Falls

\frac{d}{a} > 0

ist, gibt es damit die beiden Lösungen

x_{1} = s - \sqrt{\frac{d}{a}}, x_{2} = s + \sqrt{\frac{d}{a}}

der Gleichung; diese liegen symmetrisch um die

x

-Koordinate

s

des Scheitelpunkts. Für

d = 0

gibt es nur eine Lösung.

Das Vorzeichen von

a

bestimmt, ob der Funktionsausdruck eine nach oben oder unten geöffnete Parabel beschreibt.

Die quadratische Gleichung hat nur eine einzige Lösung

s

, falls sie sich in die Form

(x - s)^{2} = 0

bringen lässt.

Info 2.1.25

Beliebige quadratische Gleichungen kann man (ggf. Sortieren der Terme auf die linke Seite und Normieren) durch quadratische Ergänzung in Scheitelpunktform bringen. Dazu wird auf beiden Seiten eine Konstante addiert, so dass links ein Term der Form

x^{2} \pm 2 s x + s^{2}

für die erste oder zweite binomische Formel entsteht.

Beispiel 2.1.26
Die Gleichung

x^{2} - 4 x + 2 = 0

kann man durch Addieren der Konstanten

2

in die Form

x^{2} - 4 x + 4 = 2

bzw. in die Scheitelpunktform

(x - 2)^{2} = 2

bringen. Aus ihr kann man sofort die Lösungen

x_{1} = 2 - \sqrt{2}

und

2 + \sqrt{2}

ablesen. Andererseits besitzt die quadratische Gleichung

x^{2} + x = - 2

keine Lösung, denn die quadratische Ergänzung führt auf

x^{2} + x + \frac{1}{4} = - \frac{7}{4}

bzw.

(x + \frac{1}{2})^{2} = - \frac{7}{4}

mit negativer rechter Seite bei

a = 1

Aufgabe 2.1.27
Bestimmen Sie die Lösungen dieser quadratischen Gleichungen über quadratische Ergänzung, nachdem Sie die Terme auf die linke Seite sortiert und normiert (d.h.

a = 1

gewählt) haben:

$x^{2} = 8 x - 1$ hat die Scheitelpunktform $=$ .
Die Lösungsmenge ist $L$ $=$ .
$x^{2} = 2 x + 2 + 2 x^{2}$ hat die Scheitelpunktform $=$ .
Die Lösungsmenge ist $L$ $=$ .
$x^{2} - 6 x + 18 = - x^{2} + 6 x$ hat die Scheitelpunktform $=$ .
Die Lösungsmenge ist $L$ $=$ .

Mengen können in der Form ${$ a;b;c; $\dots}$ eingegeben werden. Die leere Menge kann als

{}

eingegeben werden.

Die Umformungen lauten:

\begin{matrix} x^{2} = 8 x - 1 \\ \Leftrightarrow & x^{2} - 8 x + 1 = 0 \\ \Leftrightarrow & x^{2} - 8 x + 16 = 15 \\ \Leftrightarrow & (x - 4)^{2} = 15 \\ L = {4 - \sqrt{15}; 4 + \sqrt{15}} \end{matrix}

sowie für die zweite Gleichung

\begin{matrix} x^{2} = 2 x + 2 + 2 x^{2} \\ \Leftrightarrow & x^{2} + 2 x + 2 = 0 \\ \Leftrightarrow & x^{2} + 2 x + 1 = - 1 \\ \Leftrightarrow & (x + 1)^{2} = - 1 \\ L = {} \end{matrix}

und für die dritte Gleichung

\begin{matrix} x^{2} - 6 x + 18 = - x^{2} + 6 x \\ \Leftrightarrow & 2 x^{2} - 12 x + 18 = 0 \\ \Leftrightarrow & x^{2} - 6 x + 9 = 0 \\ \Leftrightarrow & (x - 3)^{2} = 0 \\ L = {3} . \end{matrix}