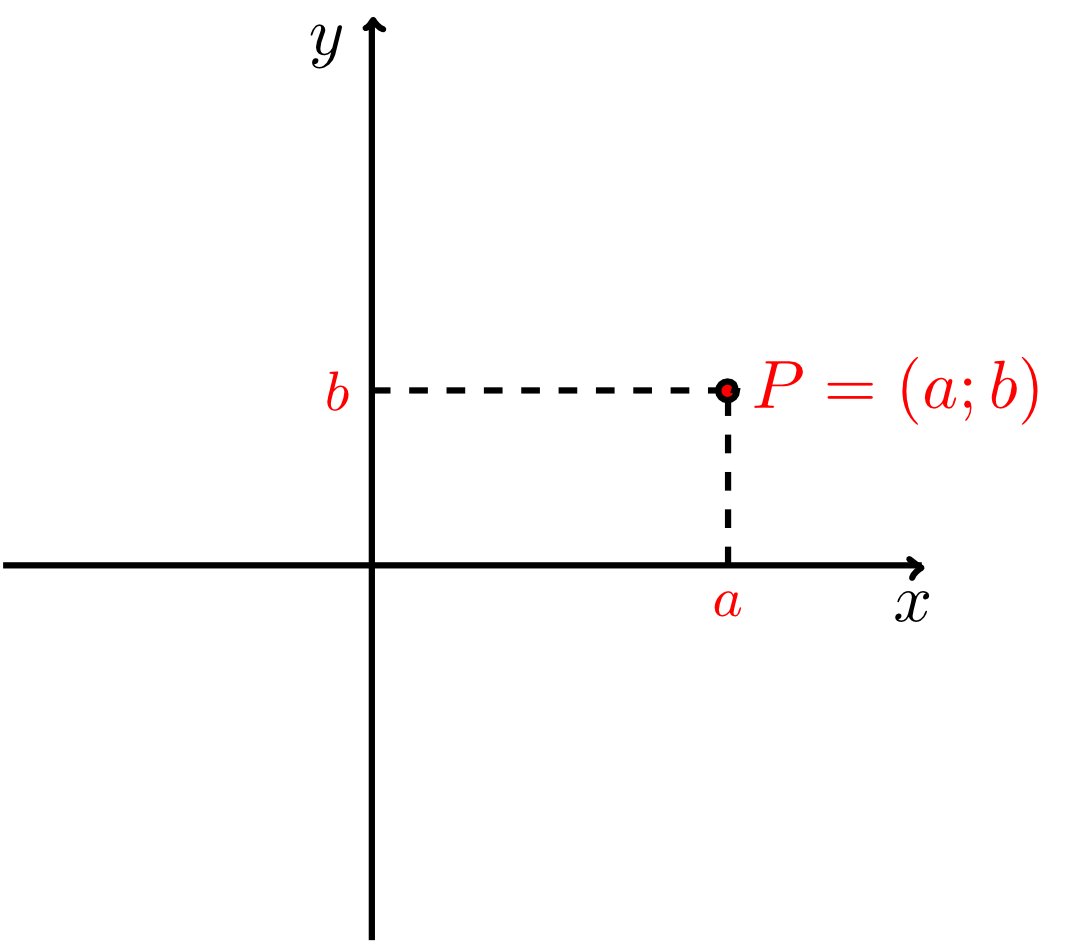Kapitel 9 Orientierung im zweidimensionalen Koordinatensystem - Abschnitt 9.1 Kartesische Koordinatensysteme in der Ebene
9.1.2 Punkte in kartesischen Koordinatensystemen
Wenn man nun Punkte in der Ebene durch Koordinaten beschreiben möchte, benutzt man auch hier oft Variablen. Typischerweise sind dies Großbuchstaben oder für Punkte und Kleinbuchstaben oder für ihre Koordinaten. Zunächst wird nun festgelegt, was unter einem Punkt in der Ebene, in welcher ein Koordinatensystem gegeben ist, zu verstehen sein soll und welche Schreibweisen dafür im Folgenden benutzt werden.
Für Punkte gibt es verschiedene Notationen. In der Schule wird oft statt geschrieben, oft statt dem Semikolon ein Trennstrich oder ein Komma als Trennzeichen zwischen den Koordinaten benutzt. In diesem Kurs wird durchgehend die Bezeichnung verwendet. Da Punkte durch ihre Koordinaten eindeutig bestimmt werden, wird im Folgenden nicht mehr zwischen dem Punkt und seinen Koordinaten unterschieden, sondern beide werden als das gleiche Objekt aufgefasst. Ein besonderer Punkt in jedem Koordinatensystem ist natürlich der Ursprung mit dem Koordinatenpaar ; für diesen wird üblicherweise die Variable (vom englischen origin) reserviert, also: .
Aufgabe 9.1.3
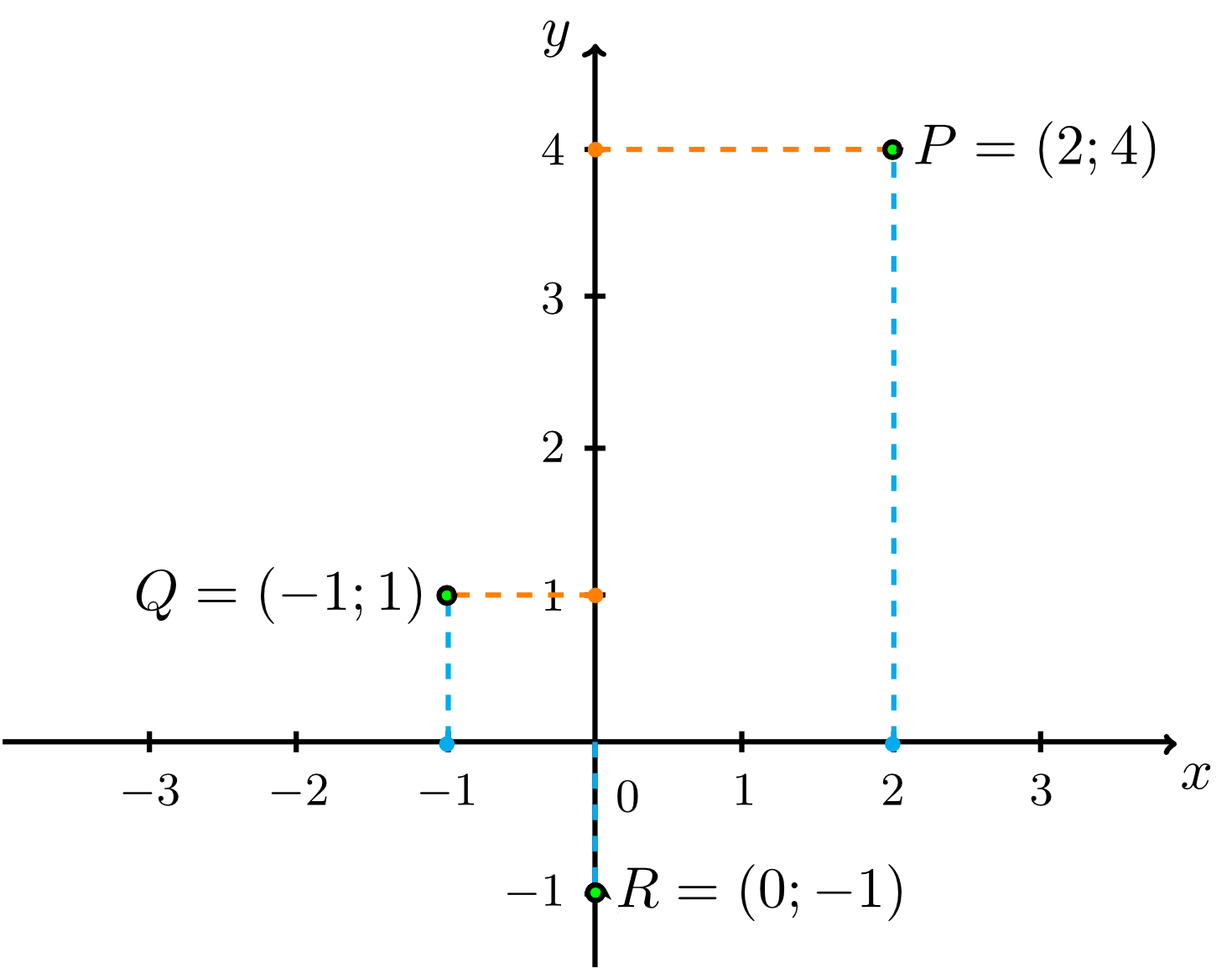
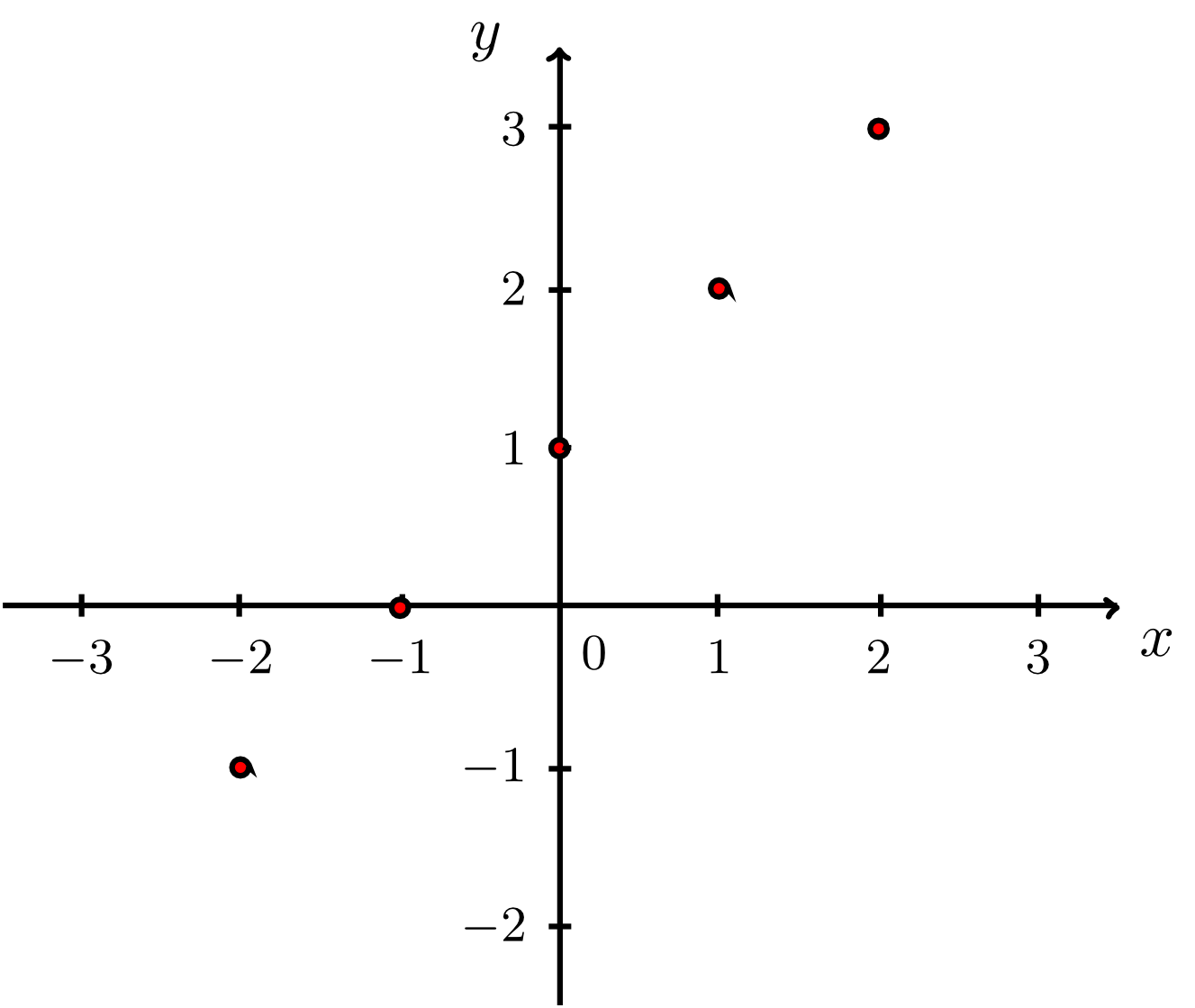
Geben Sie die Koordinaten der im folgenden Koordinatensystem eingezeichneten Punkte an.
Geben Sie die Koordinaten der im folgenden Koordinatensystem eingezeichneten Punkte an.
 .
.
 .
.
 .
.
In den folgenden Abschnitten sollen nun weitere geometrische Objekte, wie etwa Geraden und Kreise, durch Koordinaten beschrieben werden. Dafür muss man sich zunächst klarmachen, dass Punkte in der Ebene (beschrieben durch ihre Koordinaten bezüglich eines vorgegebenen Koordinatensystems) wieder zu Mengen, sogenannten Punktmengen, zusammengefasst werden können. Dies veranschaulicht das folgende Beispiel:
Aufgabe 9.1.5
Zeichnen Sie die folgenden Punktmengen in ein kartesisches Koordinatensystem ein.
Zeichnen Sie die folgenden Punktmengen in ein kartesisches Koordinatensystem ein.
-
-
- Die Menge aller Punkte im I. Quadranten mit ganzzahliger Abszisse kleiner und Ordinate
Wie aus Kapitel 5 bekannt ist, handelt es sich bei Geraden und Kreisen um Mengen von unendlich vielen Punkten. Deren Koordinaten mittels Punktmengen und geeigneten Gleichungen zu beschreiben, ist Inhalt der folgenden Abschnitte. Eine spezielle unendliche Punktmenge ist die Zusammenfassung aller Punkte in einem Koordinatensystem in der Ebene zu einer Menge. Für diese Menge gibt es eine besondere Bezeichnung:
Info
9.1.6
Die Menge aller Punkte in der Ebene, als Koordinatenpaare bezüglich eines gegebenen kartesischen Koordinatensystems, werden mit
bezeichnet. Das Symbol wird dabei als „ zwei“, „ hoch zwei“ oder „ Quadrat“ gesprochen. Dies spiegelt wieder, dass jeder Punkt durch ein Koordinatenpaar, bestehend aus zwei reellen Zahlen, beschrieben werden kann.
Die Menge aller Punkte in der Ebene, als Koordinatenpaare bezüglich eines gegebenen kartesischen Koordinatensystems, werden mit
bezeichnet. Das Symbol wird dabei als „ zwei“, „ hoch zwei“ oder „ Quadrat“ gesprochen. Dies spiegelt wieder, dass jeder Punkt durch ein Koordinatenpaar, bestehend aus zwei reellen Zahlen, beschrieben werden kann.