Onlinebrückenkurs Mathematik Abschnitt 1.1.2 Variablen und Terme

Kapitel 1 Elementares Rechnen - Abschnitt 1.1 Zahlen, Variablen, Terme

1.1.2 Variablen und Terme

Die Verwendung von Variablen, Termen und Gleichungen ist notwendig, um Aussagen mit noch unbestimmten Werten zu formalisieren.

Info 1.1.6

Eine Variable ist ein Symbol (typischerweise ein Buchstabe), das als Platzhalter für einen unbestimmten Wert eingesetzt wird. Ein Term ist ein mathematischer Ausdruck, der Variablen, Rechenoperationen und weitere Symbole enthalten kann, und der nach Einsetzung von Zahlen für die Variablen einen konkreten Zahlenwert ergibt. Terme können zu Gleichungen bzw. Ungleichungen kombiniert oder in Funktionsbeschreibungen eingesetzt werden, dazu später mehr.

Beispiel 1.1.7
Die textuelle Frage

In einer Schulklasse gibt es vier Mädchen mehr als Jungs und insgesamt 20 Kinder, wieviele Mädchen bzw. Jungs sind in der Klasse?

kann man beispielsweise formalisieren, indem man die Variablen

a

für die Anzahl der Mädchen und

b

für die Anzahl der Jungs in der Schulklasse einführt und damit die beiden Gleichungen

a = b + 4

und

a + b = 20

aufstellt. Diese kann man durch Einsetzen nun auflösen zu

a = 12

und

b = 8

und daraus den textuellen Antwortsatz

In der Schulklasse befinden sich $12$ Mädchen und $8$ Jungs

aufbauen. Dabei ist beispielsweise

b + 4

ein Term,

b

selbst ist eine Variable und

a + b = 20

ist eine Gleichung mit einem Term auf der linken und einer Zahl auf der rechten Seite.

Variablen (und manchmal Terme) werden statt mit kleinen lateinischen Buchstaben

x

y

z

, usw. oft auch mit griechischen Buchstaben bezeichnet, zum Beispiel wenn Winkel von Zahlen unterschieden werden sollen.

Info 1.1.8

Hier werden die Buchstaben des griechischen Alphabets in einer Übersicht gezeigt, die auch die Großbuchstaben enthält, sortiert nach dem griechischen Alphabet:

α

A

„alpha“

β

B

„beta“

γ

Γ

„gamma“

δ

Δ

„delta“

ε

E

„epsilon“

ζ

Z

„zeta“

η

H

„eta“

ϑ

Θ

„theta“

ι

I

„iota“

κ

K

„kappa“

λ

Λ

„lambda“

μ

M

„mü“

ν

N

„nü“

ξ

Ξ

„xi“

o

O

„omikron“

π

Π

„pi“

ϱ

P

„rho“

σ

Σ

„sigma“

τ

T

„tau“

υ

ϒ

„üpsilon“

φ

Φ

„phi“

χ

X

„chi“

ψ

Ψ

„psi“

ω

Ω

„omega“

Griechische Buchstaben können in Aufgaben mit Ihrer Bezeichnung eingegeben werden, z. B. alpha statt

α

Bei einem Term ist wesentlich, dass er zu einem konkreten Zahlenwert ausgewertet werden kann, wenn man Zahlen für die im Term auftretenden Variablen einsetzt:

Beispiel 1.1.9
Die folgenden Ausdrücke sind Terme:

$x \cdot (y + z) - 1$ , für $x = 1$ , $y = 2$ und $z = 0$ erhält man beispielsweise den Wert $1$ des Terms.
$\sin (α) + \cos (α)$ , für $α = 0^{\circ}$ und $β = 0^{\circ}$ erhält man beispielsweise den Wert $1$ (für die Berechnung von Sinus und Kosinus sei auf das Kapitel 5 verwiesen).
$1 + 2 + 3 + 4$ , es treten keine Variablen auf, trotzdem handelt es sich um einen Term (der immer den Wert $10$ ergibt).
$\frac{α + β}{1 + γ}$ , beispielsweise erhält man für $α = 1$ , $β = 2$ und $γ = 3$ den Wert $\frac{3}{4}$ für den Term. Hier darf man aber nicht $γ = - 1$ einsetzen.
$\sin (π (x + 1))$ , beispielsweise ergibt der Term den Wert Null wenn man für $x$ eine ganze Zahl einsetzt.
$z$ , eine Variable für sich allein ist auch ein Term.
$1 + 2 + 3 + \dots + (n - 1) + n$ ist ein Term, bei dem die Variable $n$ im Term auftritt und gleichzeitig seine Länge festlegt.

Beispiel 1.1.10
Diese Ausdrücke sind keine Terme im Sinne der Mathematik:

$a + b = 20$ , ist eine Gleichung (Einsetzen von Werten für $a$ und $b$ ergibt keine Zahl, sondern die Gleichung ist eben wahr oder falsch).
$a \cdot (b + c$ ist nicht richtig geklammert,
„Anteil der Mädchen in der Schulklasse“ ist kein Term, kann aber durch den Term $\frac{a}{a + b}$ formalisiert werden,
$\sin$ ist kein Term sondern ein Funktionsname, dagegen ist $\sin (α)$ ein Term (der bei Einsetzen eines Winkels für $α$ ausgewertet werden kann).

Aufgabe 1.1.11
Gegeben sind jeweils ein Term und Zahlenwerte für die im Term auftretenden Variablen. Wie lautet die Auswertung des Terms?

$\frac{α + β}{α - β}$ nimmt den Wert an für $α = 6$ und $β = 4$ .
$y^{2} + x^{2}$ nimmt den Wert an für $y = 2 x + 1$ und $x = - 1$ .
$1 + 2 + 3 + \dots + (n - 1) + n$ nimmt den Wert an für $n = 6$ .

Einsetzen der gegebenen Werte für die Variablen ergibt

\frac{α + β}{α - β} = \frac{6 + 4}{6 - 4} = \frac{10}{2} = 5

in Teil 1),

y^{2} + x^{2} = (- 1)^{2} + (- 1)^{2} = 2

in Teil 2) und

1 + 2 + 3 + 4 + 5 + 6 = 21

in Teil 3).

Aufgabe 1.1.12
Formalisieren Sie mit den vorgegebenen Variablen den Anteil der Mädchen, deren Anzahl durch die Variable

a

gegeben sei, sowie den der Jungen, deren Anzahl durch die Variable

b

gegeben sei, an der Gesamtzahl an Kindern:

Anteil der Mädchen ist

und Anteil der Jungen ist

.
Brüche können mit dem Strich (über der 7-Taste auf den meisten Tastaturen) eingegeben werden, dabei sollten Zähler bzw. Nenner geklammert werden wenn Rechenoperationen auftreten. Beispielsweise kann man den Bruch

\frac{1 + x}{2 + y}

eingeben als (1+x)/(2+y).

Die Gesamtanzahl der Kinder ist

a + b

, der Mädchenanteil ist daher

\frac{a}{a + b}

und der Jungenanteil ist

\frac{b}{a + b}

Terme können auch ineinander eingesetzt werden:

Info 1.1.13

Beim Einsetzen von Termen wird ein Term anstelle eines Symbols in einem anderen Term eingesetzt, wobei das ersetzte Symbol ggf. vorher geklammert werden muss, wenn der einzusetzende Term mehrere Ausdrücke enthält.

Beispiel 1.1.14
Setzt man in den Term

x^{2} + y^{2}

beispielsweise den Wert

x = 1 + 2 + 3

ein, so entsteht der neue Term

x^{2} + y^{2} = (1 + 2 + 3)^{2} + y^{2} = 36 + y^{2}

, und nicht etwa

1 + 2 + 3^{2} + y^{2} = 12 + y^{2}

Aufgabe 1.1.15
Welcher Term entsteht, wenn man in

x^{2} + y^{2}

Folgendes einsetzt:

Der Winkel $α$ sowohl für $x$ wie auch für $y$ : Dann ist $x^{2} + y^{2}$ $=$ .
Die Zahl $2$ für $y$ und der Term $t + 1$ für $x$ : Dann ist $x^{2} + y^{2}$ $=$ .
Der Term $z + 1$ für $x$ und der Term $z - 1$ für $y$ : Dann ist $x^{2} + y^{2}$ $=$ .

Der griechische Buchstabe

α

kann als alpha eingetippt werden.

Am sichersten ist es, die Variablen vor der Termeinsetzung zu klammern, wenn der neue Term mehrere Symbole enthält:

$x^{2} + y^{2} = α^{2} + α^{2} = 2 α^{2}$ .
$x^{2} + y^{2} = (x)^{2} + y^{2} = (t + 1)^{2} + 2^{2} = t^{2} + 2 t + 5$ .
$x^{2} + y^{2} = (x)^{2} + (y)^{2} = (z + 1)^{2} + (z - 1)^{2} = z^{2} + 2 z + 1 + z^{2} - 2 z + 1 = 2 z^{2} + 2$ .

Aufgabe 1.1.16
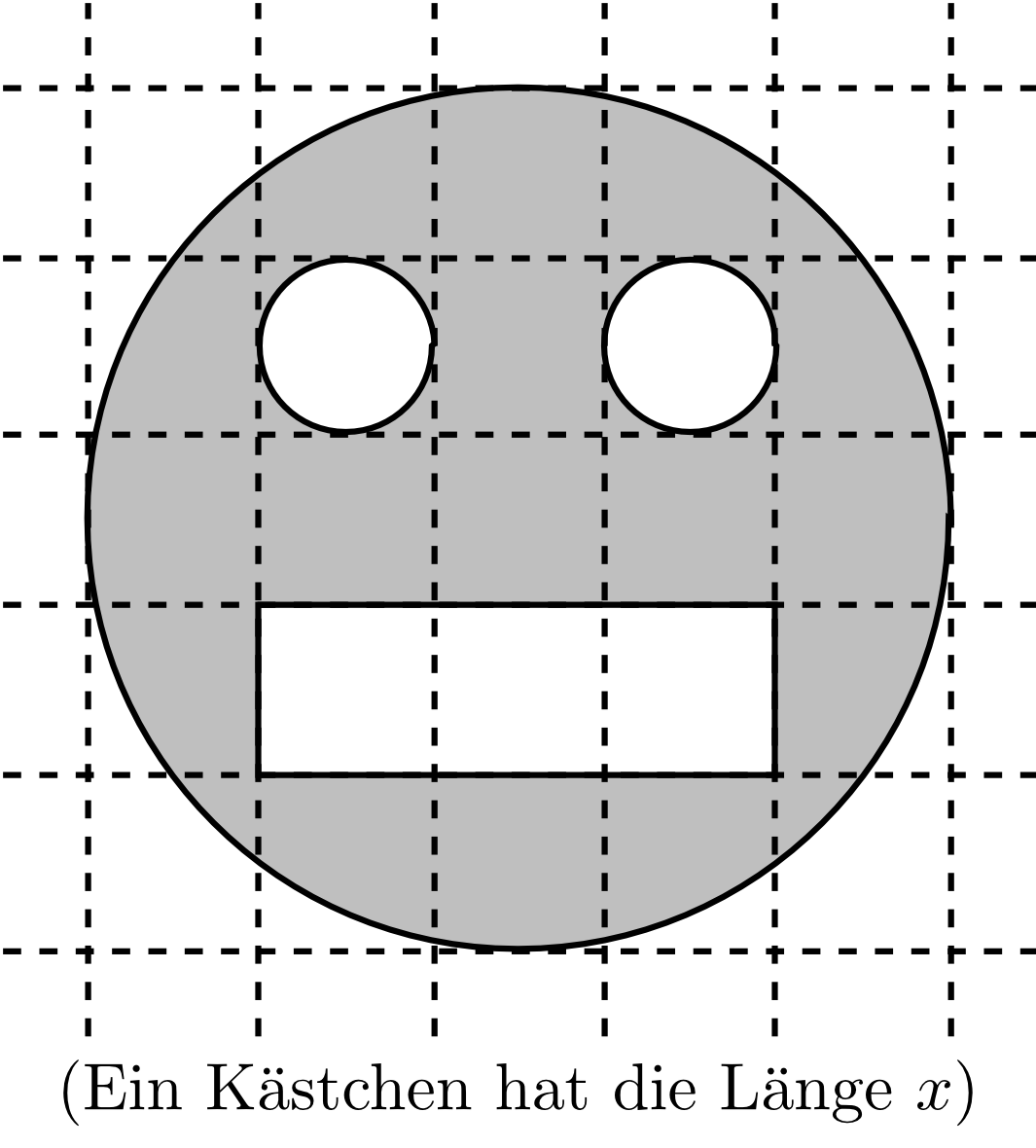
In dieser Figur habe ein Kästchen auf dem Papier die Seitenlänge

x

. Welchen Flächeninhalt (als Term in der Variablen

x

) besitzt die Figur?

Eine Figur auf kariertem Papier.

Antwort:

Der große Kreis hat insgesamt den Flächeninhalt ,
je ein kleiner Kreis hat den Flächeninhalt ,
die Figur insgesamt hat den Flächeninhalt .

Die Kreiszahl

π

kann als pi eingegeben werden.

In späteren Kapiteln wird die Berechnung von Flächen vorgestellt. Für diese Aufgabe benötigt man davon nur, dass ein Rechteck mit Seitenlängen

a

und

b

den Flächeninhalt

a \cdot b

(geschrieben a*b) besitzt, und dass ein Kreis mit Radius

r

den Flächeninhalt

π r^{2}

(geschrieben pi*r^2) besitzt.

Der große Kreis hat insgesamt den Flächeninhalt

\frac{25}{4} π x^{2}

(oder getippt 25/4*pi*x*x). Je ein kleiner Kreis hat den Flächeninhalt

\frac{1}{4} π x^{2}

und die Figur insgesamt hat den Flächeninhalt

(\frac{25}{4} π - \frac{1}{2} π - 3) \cdot x^{2}