• LEGENDE
  • 1.1
    Einführung in Thema
  • Lernabschnitt
  • Übungsaufgaben
  • Abschlusstest


  • LEGENDE
  • 1.1
    Einführung in Thema
  • Lernabschnitt
  • Übungsaufgaben
  • Abschlusstest


Kapitel 3 Ungleichungen in einer Unbekannten - Abschnitt 3.3 Betragsungleichungen und quadratische Ungleichungen

3.3.2 Quadratische Ungleichungen

Info 3.3.4  
 
Eine Ungleichung heißt quadratisch in x, falls sie sich zu x2+px+q<0 (oder mit anderen Vergleichssymbolen) umformen lässt.
 
 
Quadratische Ungleichungen kann man daher auf zwei Weisen lösen: durch Untersuchung von Nullstellen und Öffnungsverhalten des Polynoms sowie durch quadratische Ergänzung. Die quadratische Ergänzung ist meist einfacher:

Info 3.3.5  
 
Bei der quadratischen Ergänzung wird versucht, die Ungleichung auf die Form (x+a)2<b zu bringen. Ziehen der Wurzel führt dann auf die Betragsungleichung |x+a|<b mit der Lösungsmenge ]-a-b;-a+b[ falls b≥0 ist, ansonsten ist die Ungleichung unlösbar.  
 
Bei umgekehrter Richtung der Ungleichung besitzt |x+a|>b die Lösungsmenge ]-∞;-a-b[∪]-a+b;∞[. Für ≤ und ≥ sind die Randpunkte entsprechend mit aufzunehmen.


Dabei ist die Rechenregel x2=|x| aus Modul 1 zu beachten.

Beispiel 3.3.6  
Zu lösen sei die Ungleichung 2x2≥4x+2. Sortieren der Terme auf die linke Seite und Division durch 2 ergibt x2-2x-1≥0. Quadratische Ergänzung zur zweiten binomischen Formel auf der linken Seite ergibt die äquivalente Ungleichung x2-2x+1≥2, bzw. (x-1)2≥2. Ziehen der Wurzel ergibt die Betragsungleichung |x-1|≥2 mit Lösungsmenge L=]-∞;1-2]∪[1+2;∞[.


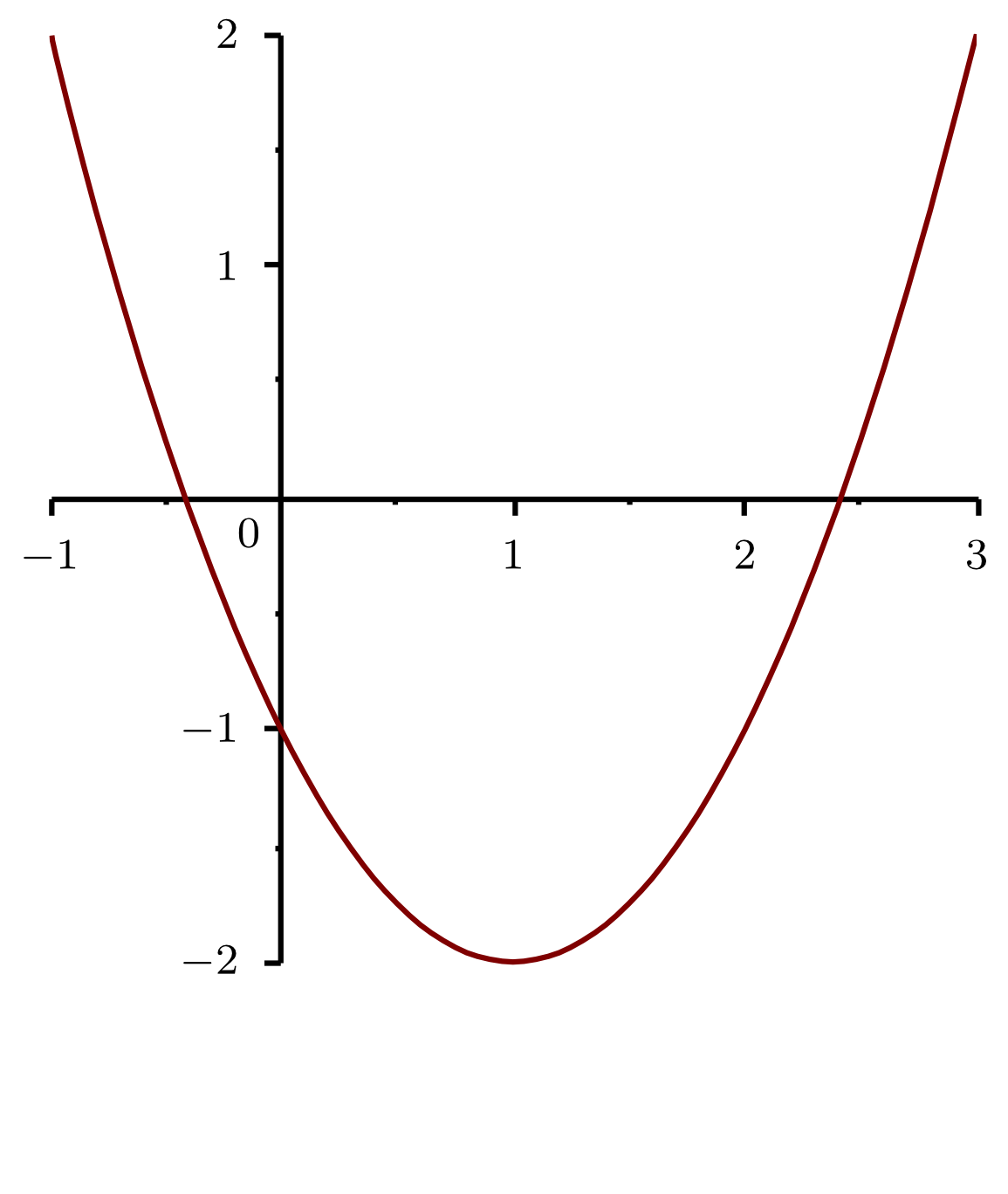
Andererseits kann man die Ungleichung x2-2x-1≥0 auch wie folgt untersuchen: Die linke Seite beschreibt eine nach oben geöffnete Parabel, deren Nullstellen x1,2=1±2 man mit der pq-Formel erhält:
./unglmtikzauto_5.4x.png
Die Ungleichung x2-2x-1≥0 wird wegen der Öffnung nach oben von den Parabelästen links und rechts von den Nullstellen erfüllt, also von der Menge L=]-∞;1-2]∪[1+2;∞[.

Info 3.3.7  
 
Die quadratische Ungleichung x2+px+q<0 (oder andere Vergleichssymbole) besitzt in Abhängigkeit der Nullstellen von x2+px+q, der Öffnung der Parabel sowie der Richtung der Ungleichung eine der folgenden Lösungsmengen:
  • die reellen Zahlen ℝ,

  • zwei Äste ]-∞;x1[∪]x2;∞[ (ggf. mit beiden Randpunkten enthalten bei ≤ und ≥),

  • ein Intervall ]x1;x2[ (ggf. mit beiden Randpunkten enthalten bei ≤ und ≥),

  • einen Einzelpunkt x1,

  • die punktierte Menge ℝ∖{x1},

  • die leere Lösungsmenge {}.



Der folgende Lückentext beschreibt die Lösung einer quadratischen Ungleichung über die Untersuchung der Parabel:

Aufgabe 3.3.8  
Zu lösen sei x2+6x<-5. Umformen ergibt die Ungleichung <0. Mit der pq-Formel findet man die Nullstellenmenge . Die linke Seite beschreibt eine nach geöffnete Parabel. Sie gehört zu einer Ungleichung mit dem Vergleichssymbol <, also ist die Lösungsmenge L =  .