Onlinebrückenkurs Mathematik Abschnitt 3.4.1 Abschlusstest Modul 3

Dies ist ein einreichbarer Test:

Im Gegensatz zu den offenen Aufgaben werden beim Eingeben keine Hinweise zur Formulierung der mathematischen Ausdrücke gegeben.
Der Test kann jederzeit neu gestartet oder verlassen werden.
Der Test kann durch die Buttons am Ende der Seite beendet und abgeschickt, oder zurückgesetzt werden.
Der Test kann mehrfach probiert werden. Für die Statistik zählt die zuletzt abgeschickte Version.

Aufgabe 3.4.1
Bestimmen Sie den Parameter

α

, so dass die Ungleichung

2 x^{2} \leq x - α

genau eine Lösung hat:

Aufgabe 3.4.2
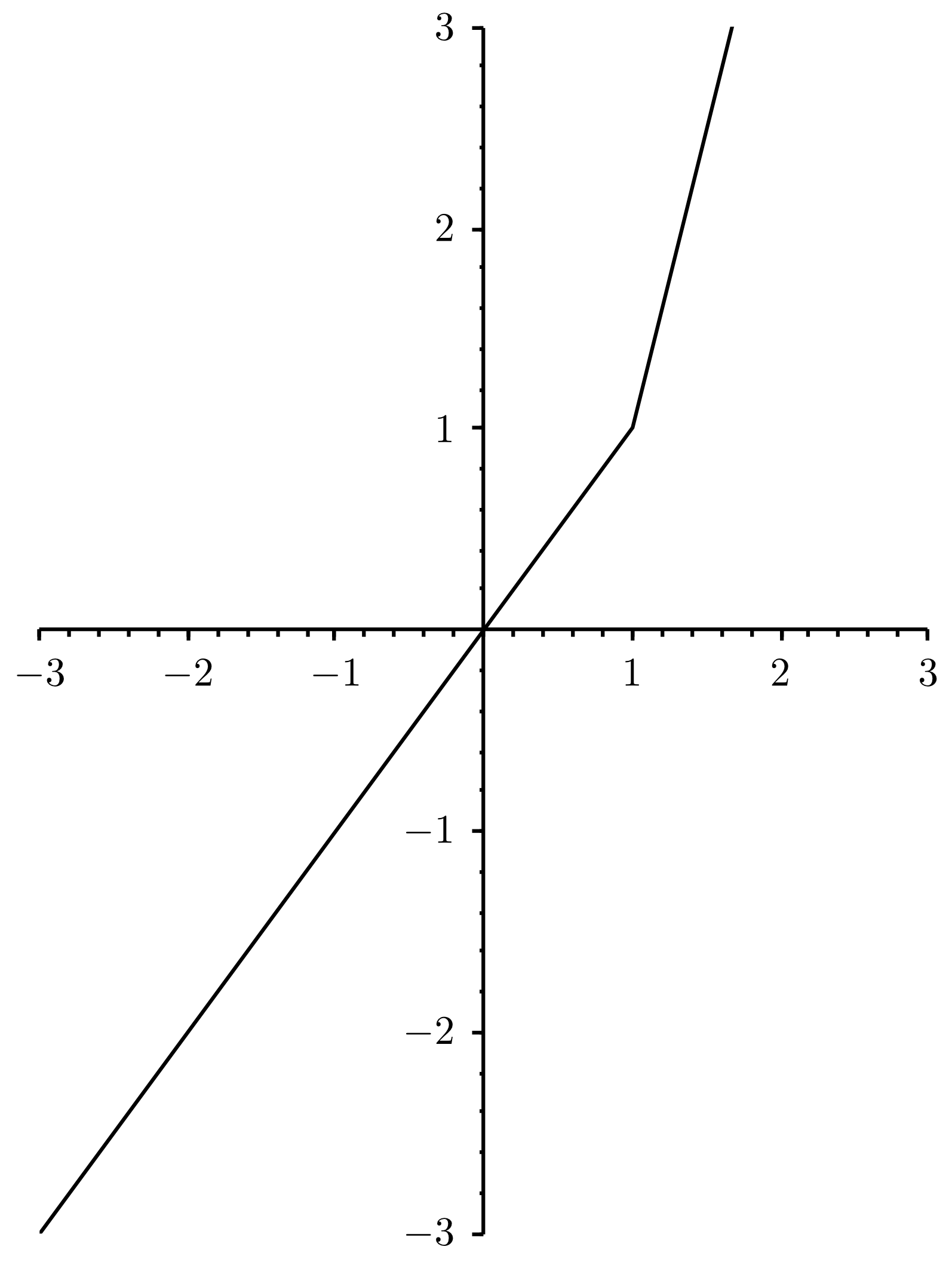
Finden Sie eine möglichst einfache Funktion

g (x)

mit einem Betragsterm, die folgenden Funktionsgraph besitzt:

Funktionsgraph von

g (x)

Versuchen Sie, eine Darstellung der Form

g (x) = | x + a | + b x + c

zu finden. Am Knick im Graph können Sie erkennen, wie der Term innerhalb des Betrags aussieht.

Bestimmen Sie anhand des Graphen die Lösungsmenge der Ungleichung $g (x) \leq x$ .
Es ist $L$ $=$ .
$g (x)$ $=$ .
Beträge können in der Form betrag(x-a) oder abs(x-a) eingegeben werden.

Aufgabe 3.4.3
Für welche positiven reellen Zahlen

x

sind die folgenden Ungleichungen erfüllt?

$| 3 x - 6 | \leq x + 2$ hat die Lösungsmenge $L$ $=$ (als Intervall geschrieben).
$\frac{x + 1}{x - 1} \geq 2$ hat die Lösungsmenge $L$ $=$ (als Intervall geschrieben).

Offene Intervalle können in der Form

(3; 5)

, geschlossene Intervalle in der Form

[3; 5]

eingegeben werden. Unendlich kann man als Wort oder kurz als infty schreiben. Verwenden Sie nicht die Schreibweise

] a; b [

für offene Intervalle. Mengen können in aufzählender Form

{1; 2; 3}

eingegeben werden. Die Mengenklammer erhalten Sie mit AltGr+7 bzw. AltGr+0.

Hier erscheint die Testauswertung!