Onlinebrückenkurs Mathematik Abschnitt 4.4.3 Aufgaben

Kapitel 4 Lineare Gleichungssysteme - Abschnitt 4.4 Allgemeinere Systeme

4.4.3 Aufgaben

Aufgabe 4.4.3
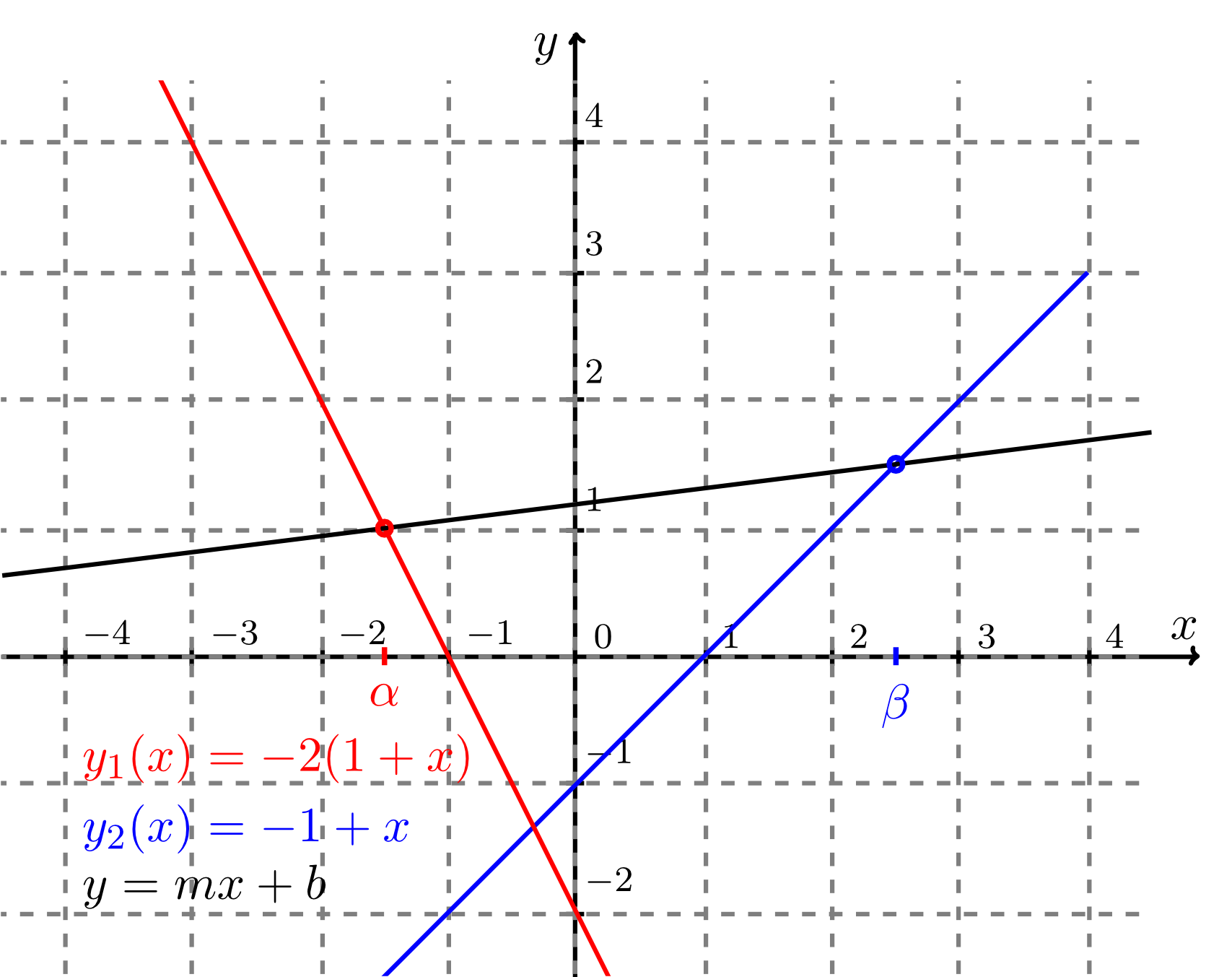
Es sollen der Achsenabschnitt

b

und die Steigung

m

einer Geraden mit der Darstellung

y = m x + b

bestimmt werden, welche durch zwei Punkte festgelegt wird. Der erste Punkt an der Stelle

x_{1} = α

liegt auf der Geraden, welche durch die Gleichung

y_{1} (x) = - 2 (1 + x)

beschrieben wird; der zweite Punkt an der Stelle

x_{2} = β

liegt auf der Geraden, die durch

y_{2} (x) = x - 1

beschrieben wird. Die Situation wird durch die nachfolgende Graphik verdeutlicht.

Bestimmen Sie das Gleichungssystem für die Geradenparameter $b$ und $m$ .

Die erste Gleichung lautet $m α + b$ $=$ ;
die zweite Gleichung lautet $m β + b$ $=$ .
Die Konstanten $α$ und $β$ müssen in der Lösung stehen bleiben; für diese kann man alpha und beta eingeben.
Lösen Sie dieses Gleichungssystem für $b$ und $m$ . Für welche $α$ und $β$ ergibt sich eine eindeutige, keine bzw. unendlich viele Lösungen?

Z.B. erhält man für den Fall $α = - 2$ und $β = 2$ die Lösung $m$ $=$ und $b$ $=$ , für den Fall $α = 2$ und $β = - 2$ ergibt sich die Lösung $m$ $=$ und $b$ $=$ .

Das LGS besitzt unendlich viele Lösungen, falls $α$ $=$ und $β$ $=$ ist.
Die zugehörigen Lösungen lassen sich parametrisieren mit $m = r$ und $b$ $=$ , $r \in ℝ$ .
Was bedeuten die letzten beiden Fälle, d.h. keine bzw. unendlich viele Lösungen, anschaulich?

Das LGS für $m$ und $b$ ergibt sich aus den Bedingungen

$y (x_{1} = α) = y_{1} (x_{1} = α) und y (x_{2} = β) = y_{2} (x_{2} = β)$
zu

$\begin{matrix} m α + b & = & - 2 (1 + α) & Gl. (1), \\ m β + b & = & - 1 + β & Gl. (2) . \end{matrix}$
Ersetzt man Gl. (2) durch die Differenz von Gl. $(2)$ und Gl. $(1)$ , dann erhält man

$\begin{matrix} m α + b & = & - 2 (1 + α) & Gl. (1), \\ m (β - α) & = & 1 + 2 α + β & Gl. (2') . \end{matrix}$
Das LGS liegt damit bereits in Dreiecksform vor.

A. Für den Fall $β - α \neq 0 \Leftrightarrow β \neq α$ kann Gl. $(2')$ durch $(β - α)$ dividiert werden, womit man die Steigung $m$ zu

$m = \frac{1 + 2 α + β}{β - α}$
erhält. Dieses Ergebnis kann man z.B. in die nach $b$ aufgelöste Gl. (1) einsetzen:

$b = - 2 (1 + α) - m α = - 2 (1 + α) - \frac{1 + 2 α + β}{β - α} α .$
Die so gefundenen Werte für $m$ und $b$ stellen eine eindeutige Lösung des betrachteten LGS dar.

Für das Beispiel $α = - 2, β = 2$ erhält man die Lösung $m = - 1 / 4, b = 5 / 2$ und für $α = 2, β = - 2$ das Ergebnis $m = - 3 / 4, b = - 9 / 2$ .

B. In diesem Fall gilt $β - α = 0 \Leftrightarrow β = α$ . Damit verschwindet die linke Seite von Gl. $(2')$ . Dies macht die folgende weitere Fallunterscheidung nötig:

Ba. Gilt nun für die rechte Seite von Gl. $(2')$ $1 + 2 α + β \neq 0$ , dann besitzt das LGS keine Lösung, $L = ∅$ . Setzt man noch $β = α$ ein, dann erhält man $β = α \neq - \frac{1}{3}$ .

Bb. Verschwindet die rechte Seite von Gl. $(2')$ , dann besteht das LGS faktisch nur noch aus Gl. (1) mit $β = α = - \frac{1}{3}$ . In diesem Fall kann man $m = λ$ , $λ \in ℝ$ , beliebig vorgeben, und $b$ ergibt sich direkt aus Gl. (1) zu $b = \frac{1}{3} λ - \frac{4}{3}$ . Die Lösungsmenge stellt sich damit wie folgt dar:

$L = {(m = λ; b = \frac{1}{3} λ - \frac{4}{3}) : λ \in ℝ} .$
Die rechten Seiten der Gln. $(1)$ und $(2)$ enthalten die $y$ -Werte der Ausgangsgeraden an den Stellen $α$ und $β$ , d.h. $y_{1} (α)$ und $y_{2} (β)$ , sodass in Gl. $(2')$ auf der rechten Seite die Differenz $y_{2} (β) - y_{1} (α)$ steht. Im Fall 2., $β = α$ , erhält man dann $y_{2} (α) - y_{1} (α)$ . Das LGS hat also keine Lösung (Fall 2a), wenn dann $y_{2} (α) - y_{1} (α) \neq 0$ $\Leftrightarrow$ $y_{2} (α) \neq y_{1} (α)$ gilt, die beiden Geraden also verschiedene $y$ -Werte besitzen. Dahingegen existieren unendlich viele Lösungen (Fall 2b), wenn sich die beiden Ausgangsgeraden an der Stelle $α$ schneiden.

Aufgabe 4.4.4
Bestimmen Sie für das folgende parameterabhängige LGS die Lösungsmenge für alle

t \in ℝ

\begin{matrix} x - y + t z & = & t & Gl. (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & Gl. (2), \\ (1 - t) x + (- 2 + t) y + (- 1 + t - t^{2}) z & = & t^{2} & Gl. (3) . \end{matrix}

Das LGS besitzt Lösungen nur für folgende Werte des Parameters:

t \in

.
Mengen können in der Form ${$ a;b;c; $\dots}$ eingegeben werden. Die leere Menge kann als

{}

eingegeben werden.

Für den kleinsten dieser Parameterwerte kann die Lösung angegeben werden durch:

x

=

y

=

z = r

r \in ℝ

.
Für den größten dieser Parameterwerte kann die Lösung angegeben werden durch:

x

=

y

=

z = r

r \in ℝ

In einem ersten Schritt kann man Gl.

(2)

zu Gl.

(3)

addieren und damit Gl.

(3)

ersetzen:

\begin{matrix} x - y + t z & = & t & Gl. (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & Gl. (2), \\ x - y + t z & = & - 1 + t + t^{2} & Gl. (3') . \end{matrix}

Da die linken Seiten der Gln.

(1)

und

(3')

übereinstimmen, bietet es sich an, das Negative von Gl.

(1)

zu Gl.

(3')

zu addieren und damit Gl.

(3')

zu ersetzen:

\begin{matrix} x - y + t z & = & t & Gl. (1), \\ t x + (1 - t) y + (1 + t^{2}) z & = & - 1 + t & Gl. (2), \\ 0 & = & - 1 + t^{2} & Gl. (3'') . \end{matrix}

Nachfolgend erhält man für das LGS eine Dreiecksform, wenn man das

(- t)

-fache von Gl.

(1)

zu Gl.

(2)

hinzuaddiert und damit Gl.

(2)

ersetzt:

\begin{matrix} x - y + t z & = & t & Gl. (1), \\ y + z & = & - 1 + t - t^{2} & Gl. (2'), \\ 0 & = & - 1 + t^{2} & Gl. (3'') . \end{matrix}

Schließlich führt die Addition von Gl.

(2')

zu Gl.

(1)

zur einer weiteren Vereinfachung,

\begin{matrix} x + (1 + t) z & = & - 1 + 2 t - t^{2} & Gl. (1'), \\ y + z & = & - 1 + t - t^{2} & Gl. (2'), \\ 0 & = & - 1 + t^{2} & Gl. (3'') . \end{matrix}

Dieses äquivalente LGS besitzt nur dann eine Lösung, wenn auch Gl.

(3'')

erfüllt ist, also

0 = - 1 + t^{2}

\Leftrightarrow

t^{2} = 1

gilt. In allen anderen Fällen ist die Lösungsmenge leer, d.h.

L = ∅ für t \in ℝ ∖ {- 1; 1} .

Ist nun Gl.

(3'')

erfüllt, also

t = 1

oder

t = - 1

, dann kann

z

frei gewählt werden, d.h.

z = λ

λ \in ℝ

. Die Umstellung der Gln.

(1')

und

(2')

nach

x

bzw.

y

liefert im Fall

t = 1

die Ausdrücke

x = - 2 z

und

y = - 1 - z

, also

L = {(x = - 2 λ; y = - 1 - λ; z = λ) : λ \in ℝ} für t = 1 .

Entsprechend ergeben sich im Fall

t = - 1

die Ausdrücke

x = - 4

und

y = - 3 - z

, also

L = {(x = - 4; y = - 3 - λ; z = λ) : λ \in ℝ} für t = - 1 .