• LEGENDE
  • 1.1
    Einführung in Thema
  • Lernabschnitt
  • Übungsaufgaben
  • Abschlusstest


  • LEGENDE
  • 1.1
    Einführung in Thema
  • Lernabschnitt
  • Übungsaufgaben
  • Abschlusstest


Kapitel 8 Integralrechnung - Abschnitt 8.3 Anwendungen

8.3.2 Flächenberechnung

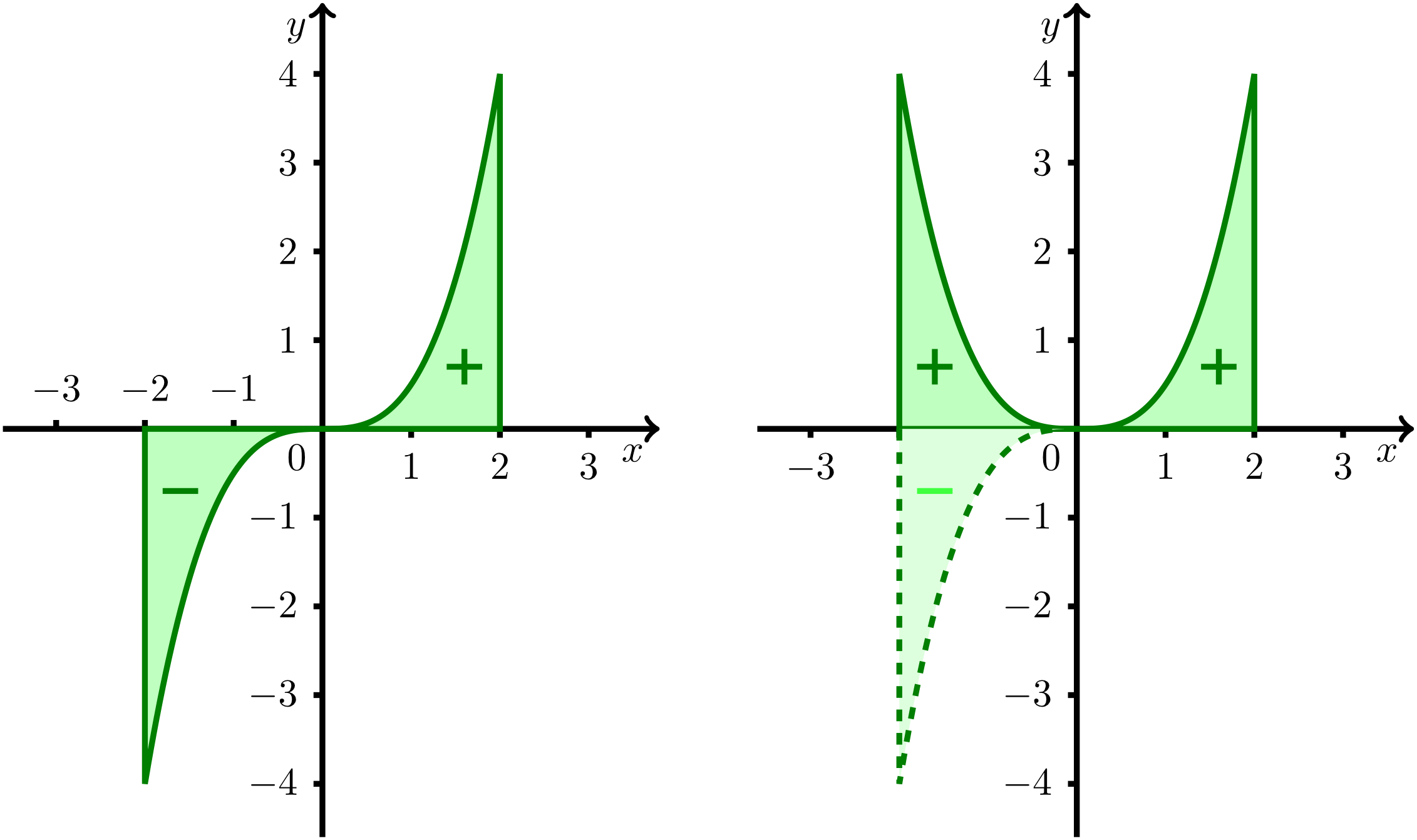
Eine erste Anwendung der Integrationsrechnung ist die Berechnung von Flächeninhalten, deren Ränder von mathematischen Funktionen beschrieben werden können. Zur Veranschaulichung ist in der folgenden Abbildung (linkes Bild) die Funktion f(x)=12x3 auf dem Intervall [-2;2] dargestellt. Das Ziel ist die Berechnung des Flächeninhalts, der vom Graphen der Funktion und der x-Achse eingeschlossen wird. Die bisherigen Untersuchungen ergeben, dass das Integral über diese ungerade Funktion in den Grenzen von -2 bis 2 genau Null ergeben wird, da die linke und rechte Teilfläche gleich groß sind, aber bei der Integration unterschiedliche Vorzeichen erhalten. Das Integral entspricht hier also nicht dem Wert des Flächeninhalts. Spiegelt man jedoch die ,,negative'' Fläche an der x-Achse, gibt man der Funktion also ein positives Vorzeichen (rechtes Bild), dann kann man den Flächeninhalt richtig bestimmen. Mathematisch bedeutet das, dass man nicht das Integral der Funktion f berechnet, sondern das Integral des Betrags |f|.

./VBKM08mtikzauto_6.4x.png


Durch die Bildung des Betrags der Funktion benötigt man eine Aufteilung des Integrals in die Bereiche mit positivem und negativem Vorzeichen. Für die Berechnung heißt dies, dass man das Integrationsintervall in Abschnitte zu unterteilt, in denen die Funktionswerte dasselbe Vorzeichen haben. Für stetige Funktionen ergeben sich diese durch die Nullstellen der Funktion.

Flächenberechnung 8.3.1  
Gegeben ist eine stetige Funktionen f:[a;b]→ℝ auf einem Intervall [a;b]. Weiter seien x1 bis xm die Nullstellen von f mit x1<x2<…<xm. Es werden x0:=a und xm+1:=b gesetzt.

Dann ist der Flächeninhalt zwischen dem Graphen von f und der x-Achse gleich

∫ab|f(x)| dx=∑k=0m|∫xkxk+1f(x) dx| .



Dies soll für das oben dargestellte Beispiel etwas genauer erörtert werden.

Beispiel 8.3.2  
Zu berechnen ist der Flächeninhalt IA der Fläche, den die stetige Funktion f mit f(x)=12x3 im Bereich [-2;2] mit der x-Ache einschließt. Die einzige Nullstelle der gegebenen Funktion befindet sich bei x0=0. Man teilt den Integrationsbereich also in die beiden Teilintervalle [-2;0] und [0;2] auf und berechnet mit

IA=∫-22|12x3|dx=|∫-2012x3 dx|+|∫0212x3 dx|=|[18x4]-20|+|[18x4]02|=|0-2|+|2-0|=4

den Flächeninhalt zwischen Kurve und x-Achse zu IA=4.


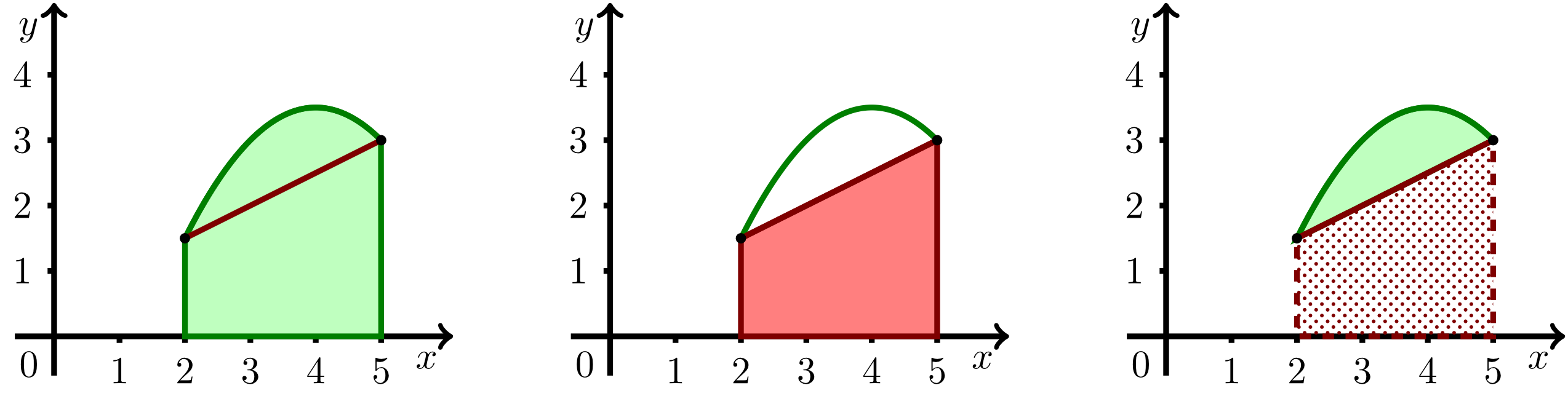
Man kann nicht nur Flächeninhalte zwischen einer Kurve und der x-Achse bestimmen, sondern auch den Inhalt einer Fläche, die von zwei Kurven eingeschlossen wird, wie in der folgenden Abbildung veranschaulicht wird. Dort zeigt das rechte Bild die gesuchte Fläche, deren Flächeninhalt als die Differenz der Flächeninhalte aus dem linken und dem mittleren Bild berechnet wird.

./VBKM08mtikzauto_7.4x.png


Dieses Prinzip soll ebenfalls zuerst formal vorgestellt und danach an einem Beispiel erläutert werden.

Flächenberechnung zwischen den Graphen zweier Funktionen 8.3.3  
Gegeben sind zwei stetige Funktionen f,g:[a;b]→ℝ auf einem Intervall [a;b]. Weiter seien x1 bis xm die Nullstellen von f-g mit x1<x2<…<xm. Es werden x0:=a und xm+1:=b gesetzt.

Dann kann der Flächeninhalt zwischen dem Graphen von f und dem von g durch

∫ab|f(x)-g(x)| dx=∑k=0m|∫xkxk+1(f(x)-g(x)) dx|

berechnet werden.


Dazu soll nun ein Beispiel betrachtet werden.

Beispiel 8.3.4  
Berechnet werden soll der Inhalt IA der Fläche zwischen den Graphen von f und g mit f(x)=x2 und g(x)=8-14x4 für x∈[-2;2]. Zunächst untersucht man die Differenz f-g der Funktionen auf ihre Nullstellen. Mit

f(x)-g(x)=14x4+x2-8=14(x4+4x2-32)=14(x4+4x2+22-22-32)=14((x2+2)2-36)

kann man die reellen Nullstellen von f-g berechnen:

(x2+2)2-36=0⇔(x2+2)2=36⇔x2+2=6⇔x2=4⇔x=±2

oder mit der dritten binomischen Formel:

0=(x2+2)2-36=(x2+2)2-62=(x2+2-6)·(x2+2+6)=(x2-4)·(x2+2+6)=(x-2)·(x+2)·(x2+8) .

In der ersten Rechnung wurde nach dem Ziehen der ersten Wurzel auf eine nähere Betrachtung des Falls x2+2=-6 verzichtet, da man aus der daraus folgenden Gleichung x2=-8 keine reellen Nullstellen erhält. Die reellen Nullstellen von f-g sind -2 und 2. Dies sind gleichzeitig auch die Randstellen des Intervalls [-2;2]. Eine Aufteilung des Integrals in verschiedene Bereiche ist also nicht nötig. Die Werte von f sind kleiner als die von g auf diesem Intervall. Damit erhält man den Flächeninhalt



IA=∫-22|f(x)-g(x)|dx=∫-22(g(x)-f(x))dx=∫-22(-14x4-x2+8)dx=2∫02(-14x4-x2+8)dx ,      da der Integrand gerade ist=[-120x5-13x3+8x]02=2·(-3220-83+16)=35215 .