Kapitel 7 Differentialrechnung - Abschnitt 7.4 Eigenschaften von Funktionen
7.4.2 Monotonie
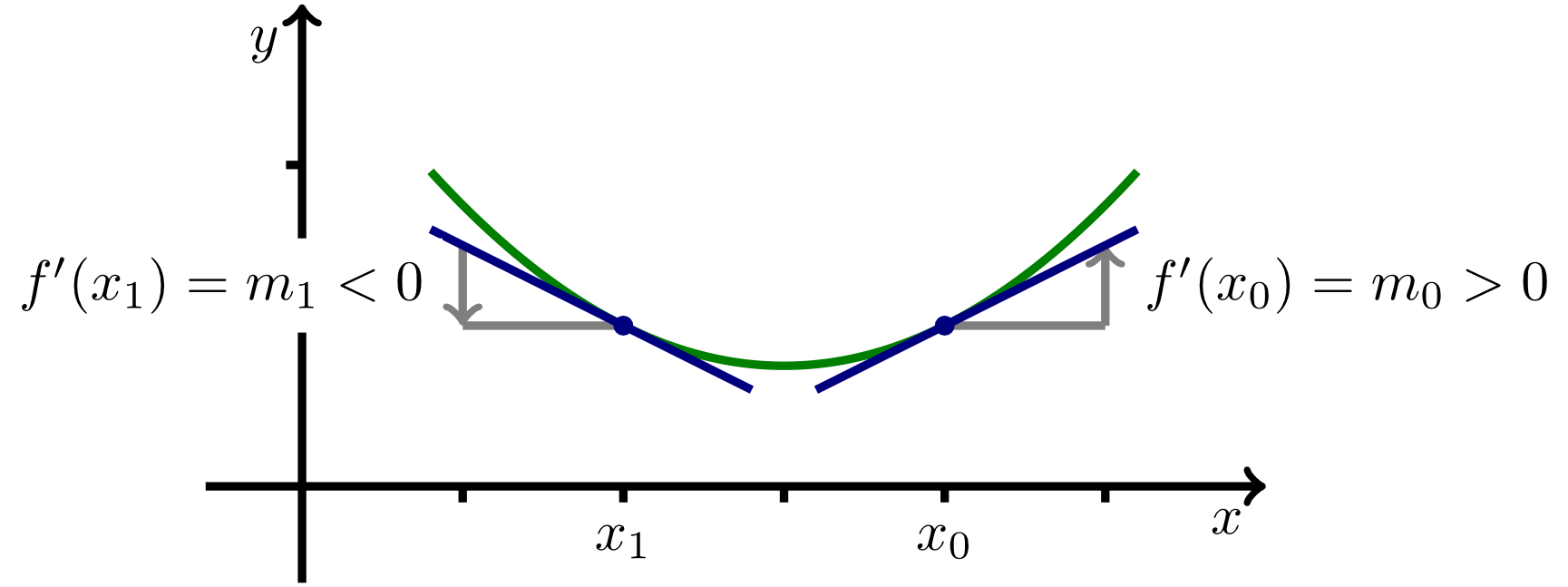
Mit der Ableitung kann das lokale Wachstumsverhalten untersucht werden, das heißt, ob für steigende Argumente die zugehörigen Funktionswerte größer oder kleiner werden. Dazu wird eine Funktion betrachtet, die auf differenzierbar ist:
Wenn für alle zwischen und gilt, dann ist auf dem Intervall monoton fallend.
Wenn für alle zwischen und gilt, dann ist auf dem Intervall monoton wachsend.
Somit genügt es, das Vorzeichen der Ableitung zu bestimmen, um zu erkennen, ob eine Funktion auf dem Intervall monoton wachsend oder monoton fallend ist.
Beispiel
7.4.1
Die Funktion ist differenzierbar mit . Da für alle gilt, ist und damit monoton wachsend.
Für mit besitzt die Nullstellen und . Zur Untersuchung des Monotonieverhaltens werden also drei Bereiche unterschieden, in denen die Ableitung jeweils ein anderes Vorzeichen hat.
Mit Hilfe folgender Tabelle wird bestimmt, in welchen Bereichen die Ableitung von positiv bzw. negativ ist. Diese Bereiche entsprechen den Monotoniebereichen von . Der Eintrag besagt, dass der betrachtete Term im angegebenen Intervall positiv ist. Wenn er negativ ist, wird eingetragen:
Für die Funktion mit gilt . Hier ist für alle .
Auch wenn für die beiden Teilbereiche und dasselbe Monotonieverhalten auftritt, ist nicht über den gesamten Definitionsbereich monoton fallend. Als Gegenbeispiel kann und angeführt werden. Hier gilt , aber auch . Dies entspricht einem wachsenden Verhalten beim Übergang vom einen zum anderen Teilbereich. Dass die Funktion auf monoton fallend ist, bedeutet also, die Einschränkung von auf dieses Intervall ist monoton fallend. Zudem ist für alle ebenfalls monoton fallend.
Die Funktion ist differenzierbar mit . Da für alle gilt, ist und damit monoton wachsend.
Für mit besitzt die Nullstellen und . Zur Untersuchung des Monotonieverhaltens werden also drei Bereiche unterschieden, in denen die Ableitung jeweils ein anderes Vorzeichen hat.
Mit Hilfe folgender Tabelle wird bestimmt, in welchen Bereichen die Ableitung von positiv bzw. negativ ist. Diese Bereiche entsprechen den Monotoniebereichen von . Der Eintrag besagt, dass der betrachtete Term im angegebenen Intervall positiv ist. Wenn er negativ ist, wird eingetragen:
Für die Funktion mit gilt . Hier ist für alle .
Auch wenn für die beiden Teilbereiche und dasselbe Monotonieverhalten auftritt, ist nicht über den gesamten Definitionsbereich monoton fallend. Als Gegenbeispiel kann und angeführt werden. Hier gilt , aber auch . Dies entspricht einem wachsenden Verhalten beim Übergang vom einen zum anderen Teilbereich. Dass die Funktion auf monoton fallend ist, bedeutet also, die Einschränkung von auf dieses Intervall ist monoton fallend. Zudem ist für alle ebenfalls monoton fallend.