Kapitel 7 Differentialrechnung - Abschnitt 7.4 Eigenschaften von Funktionen
7.4.4 Aufgaben
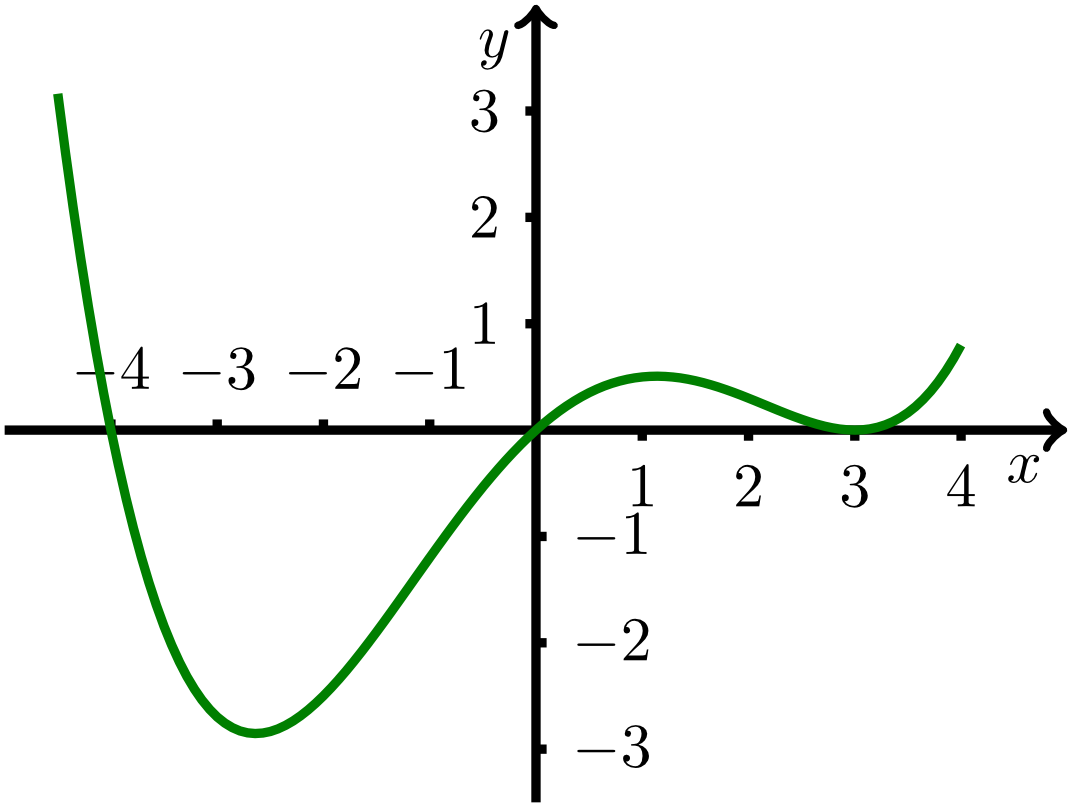
Aufgabe 7.4.5
In welchen möglichst großen offenen Intervallen ist die Funktion mit monoton wachsend beziehungsweise monoton fallend?
Antwort:
In welchen möglichst großen offenen Intervallen ist die Funktion mit monoton wachsend beziehungsweise monoton fallend?
Antwort:
- ist auf monoton
 .
.
- ist auf monoton
 .
.
Aufgabe 7.4.6
In welchen möglichst großen offenen Intervallen ist die Funktion mit für konvex beziehungsweise konkav? Antwort:
In welchen möglichst großen offenen Intervallen ist die Funktion mit für konvex beziehungsweise konkav? Antwort:
- ist auf
 konvex.
konvex.
- ist auf
 konkav.
konkav.
Aufgabe 7.4.7
Gegeben ist eine Funktion mit ; deren Ableitung besitze folgenden Graphen:
Antwort: .
Die Minimalstelle von ist bei
.
Die Minimalstelle von ist bei
 .
.
Gegeben ist eine Funktion mit ; deren Ableitung besitze folgenden Graphen:
- Wo ist monoton wachsend, wo monoton fallend?
Gesucht sind jeweils möglichst große offene Intervalle , auf
denen diese Eigenschaft hat.
- Welche Aussagen erhalten
Sie über die Maximal- beziehungsweise Minimalstellen der Funktion ?
Antwort:
- ist auf
 monoton
monoton
 .
.
- ist auf
 monoton
monoton
 .
.
- ist auf monoton
 .
.
- ist auf monoton
 .
.