Kapitel 6 Elementare Funktionen - Abschnitt 6.2 Lineare Funktionen und Polynome

6.2.2 Konstante Funktionen und die Identität

Die sogenannten konstanten Funktionen ordnen jeder Zahl aus dem Definitionsbereich $ℝ$ eine konstante Zahl aus dem Zielbereich $ℝ$ zu. Zum Beispiel die konstante Zahl $2$ auf folgende Art:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & 2\hspace{0.5em}.\hfill \end{array}}$
               

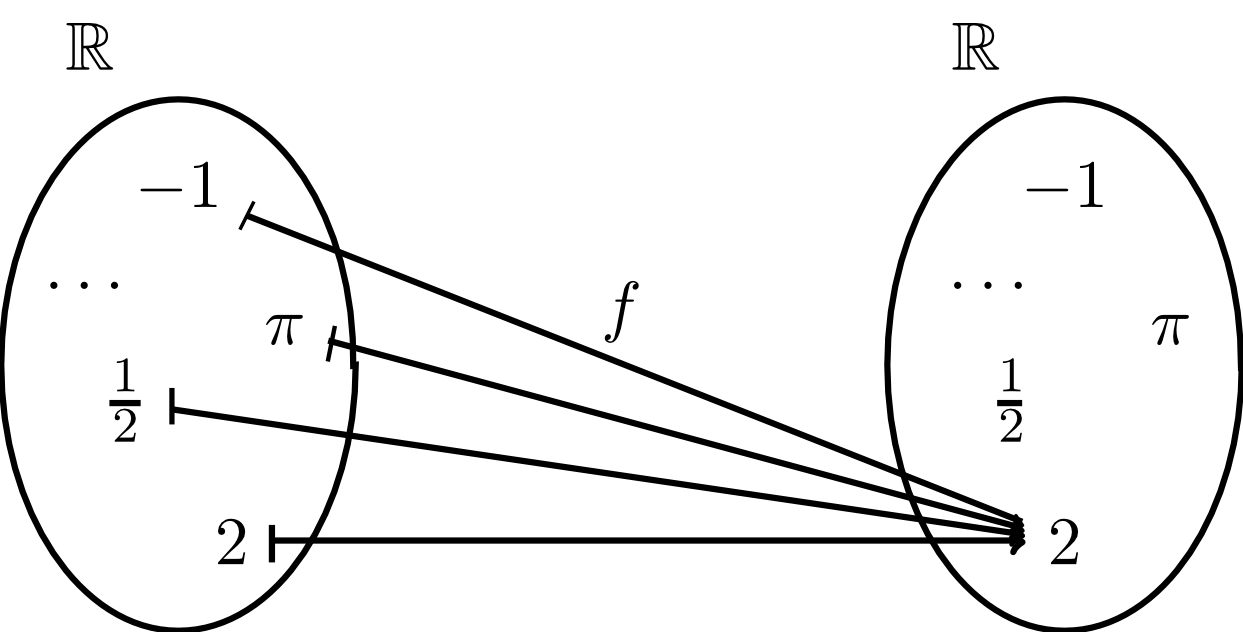
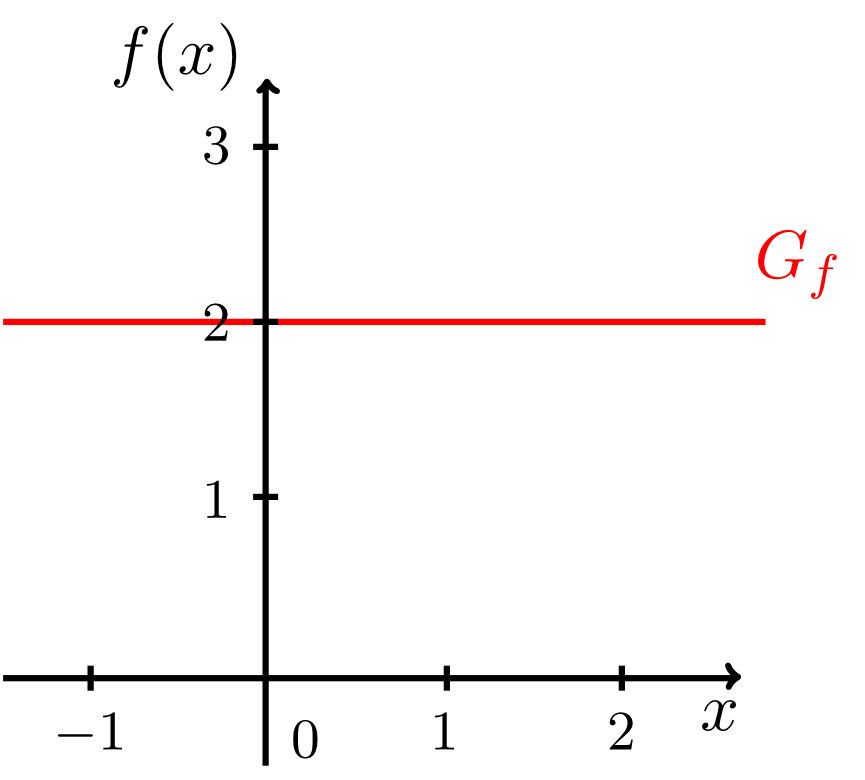
Es gilt hier also $f(x)=2$ für alle $x\in ℝ$, womit die Wertemenge dieser Funktion $f$ nur aus der Menge $W_f=\{2\}\subset ℝ$ besteht.

Die Identität auf $ℝ$ ist die Funktion, welche jeder reellen Zahl wieder genau die identische reelle Zahl zuordnet. Man schreibt das so:

${\displaystyle \mathrm{Id}:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & x\hspace{0.5em}.\hfill \end{array}}$
               

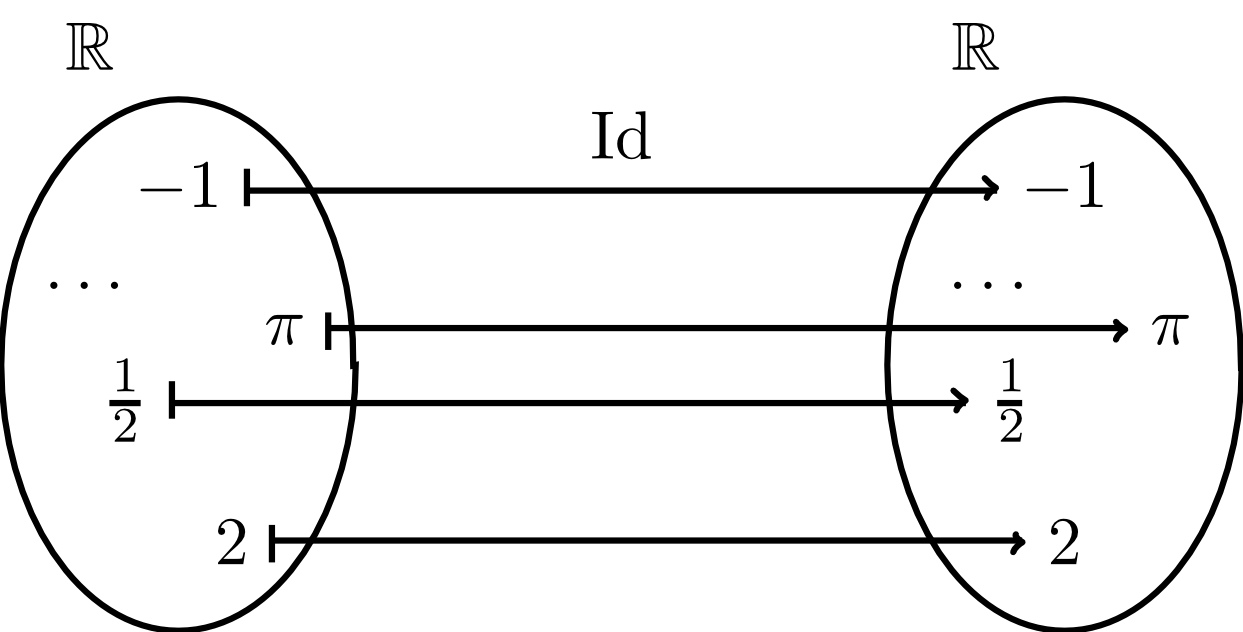
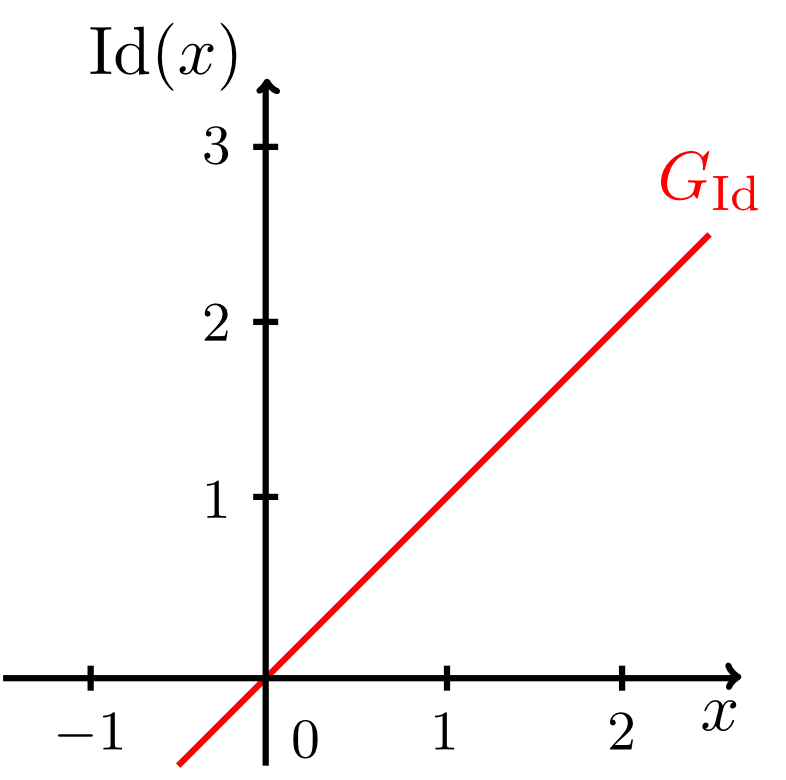
Es gilt hier also $\mathrm{Id}(x)=x$ für alle $x\in ℝ$, womit der Wertebereich von $\mathrm{Id}$ die gesamten reellen Zahlen sind ($W_{\mathrm{Id}}=ℝ$). Weiterhin ist die Identität offenbar eine streng monoton wachsende Funktion.