Kapitel 6 Elementare Funktionen - Abschnitt 6.4 Exponentialfunktion und Logarithmus

6.4.2 Inhalt

Im vorangegangen Beispiel tritt eine Exponentialfunktion zur Basis $a=2$ auf, die Veränderliche - im Beispiel $t$ - erscheint im Exponenten. Wir wollen nun die allgemeine Abbildungvorschrift für Exponentialfunktionen zu einer beliebigen Basis $a$ angeben; dabei setzen wir allerdings $a>0$ voraus:

${\displaystyle \begin{array}{cccc}\hfill f:& \hfill ℝ& \hfill \to \hfill & (0;\infty )\hfill \\ \hfill & \hfill x& \hfill ⟼\hfill & f(x)=f_0·a^{\lambda x}\hspace{0.5em}.\hfill \end{array}}$

Dabei bezeichnen $f_0$ und $\lambda$ sogenannte Parameter der Exponentialfunktion, auf die wir weiter unten eingehen werden.

Der Definitionsbereich aller Exponentialfunktionen wird von allen reellen Zahlen gebildet, $D_f=ℝ$, wohingegen der Wertebereich nur aus den positiven reellen Zahlen besteht ($W_f=(0;\infty )$), da jedwede Potenz einer postiven Zahl nur positiv sein kann.



Einige generelle Eigenschaften von Exponentialfunktionen können wir im folgenden Bild erkennen, in dem Exponentialfunktionen $g:ℝ\to (0;\infty )$, $x⟼g(x)=a^x$ für verschiedene Werte von $a$ gegenübergestellt sind:

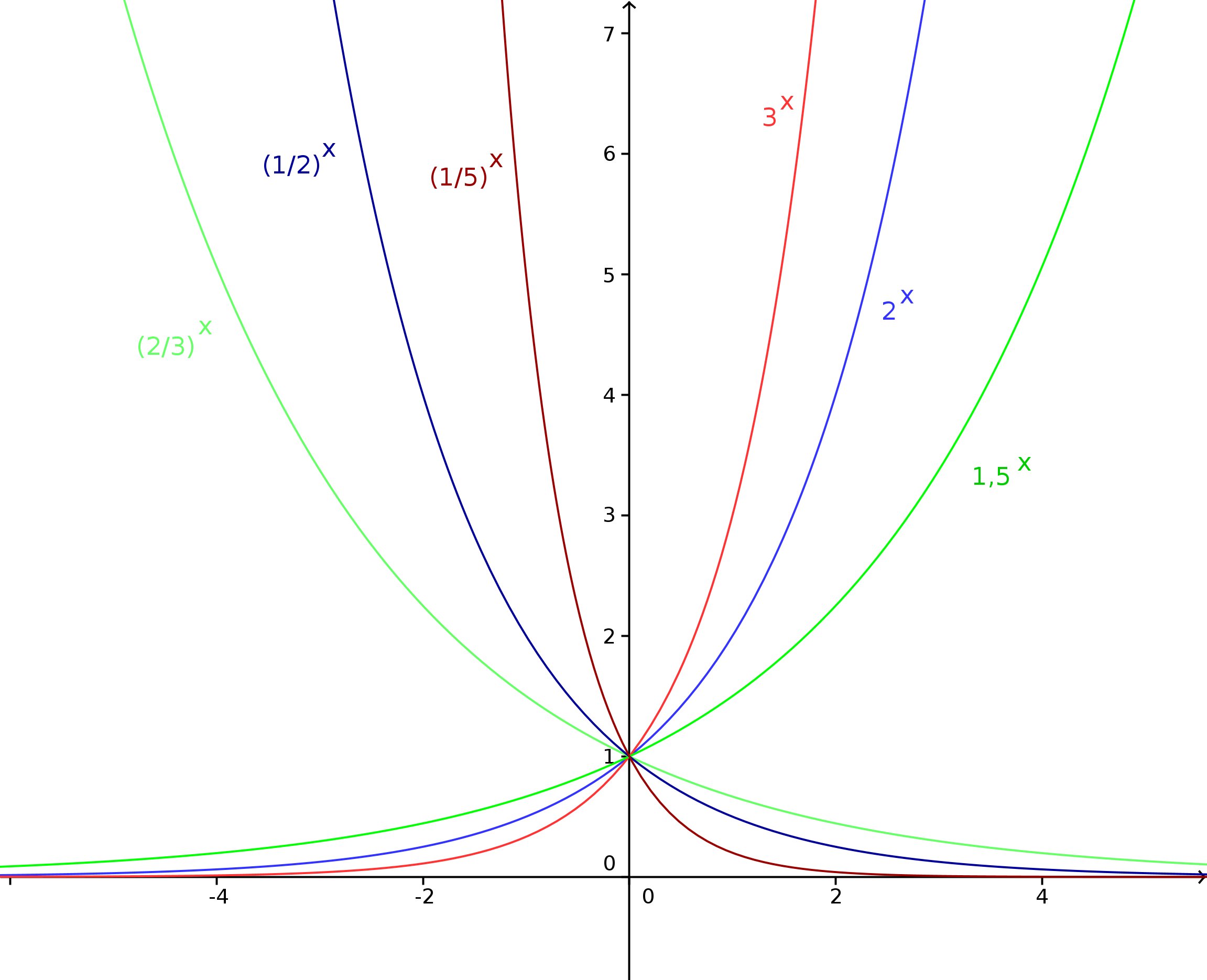
• Alle diese Exponentialfunktionen gehen durch den Punkt $(x=0,y=1)$: Dies gilt, da $g(x=0)=a^0$ und $a^0=1$ für jede Zahl $a$.
  
  
• Ist $a>1$, so steigt der Graph von $g$ von links nach rechts (also für wachsende $x$-Werte) an; man sagt auch, dass die Funktion $g$ streng monoton wachsend ist. Je größer der Wert für $a$ ist, desto schneller wächst $g$ für positive $x$-Werte. Geht man von rechts nach links (also zu immer größeren negativen $x$-Werten), so bildet die negative $x$-Achse eine Asymptote des Graphen.
  
  
• Ist $a<1$, so fällt der Graph von $g$ von links nach rechts (also für wachsende $x$-Werte) ab; man sagt auch, dass die Funktion $g$ streng monoton fallend ist. Je größer der Wert für $a$ ist, desto langsamer fällt $g$ für negative $x$-Werte. Geht man von links nach rechts (also zu immer größeren positiven $x$-Werten), so bildet die positive $x$-Achse eine Asymptote.
  
  

Und was hat es nun noch mit den Parametern $f_0$ und $\lambda$ auf sich? Der Parameter $f_0$ ist schnell erklärt: Setzt man den Wert $x=0$ für die Veränderliche in die allgemeinen Exponentialfunktionen $f$ ein,

${\displaystyle f(x=0)=f_0·a^{\lambda ·0}=f_0·a^0=f_0·1=f_0\hspace{0.5em},}$

so erkennt man, dass $f_0$ eine Art Start- oder Anfangswert darstellt (zumindest falls man die Veränderliche $x$ zeitlich interpretiert); der exponentielle Verlauf $a^{\lambda x}$ wird generell mit dem Faktor $f_0$ multipliziert und dementsprechend gewichtet, d.h. gestreckt (für $|f_0|>1$) bzw. gestaucht (für $|f_0|<1$).

Der Parameter $\lambda$ im Exponenten heißt Wachstumsrate; er bestimmt, wie stark die Exponentialfunktion - bei gleichbleibender Basis - wächst (für $\lambda >0$) oder fällt (für $\lambda <0$).