Kapitel 6 Elementare Funktionen - Abschnitt 6.2 Lineare Funktionen und Polynome

6.2.8 Hyperbeln

Wir betrachten Funktionen, die als Abbildungsvorschrift einen reziproken Zusammenhang besitzen. Darunter versteht man das Vorkommen von Kehrwerten in der Abbildungsvorschrift. Zu beachten ist bei der Bestimmung des größtmöglichen Definitionsbereichs solcher Funktionen, dass der Nenner nicht $0$ werden darf.

Beispiele reziproker Funktionen sind im Folgenden zusammengestellt; diese ergeben sich als Kehrwerte der Monome und werden auch als Funktionen vom hyperbolischen Typ bezeichnet:

${\displaystyle f_1:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x}\hspace{0.5em},\hfill \end{array}}$


${\displaystyle f_2:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^2}\hspace{0.5em},\hfill \end{array}}$


${\displaystyle f_3:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^3}\hspace{0.5em},\hfill \end{array}}$
usw. Ihre Graphen sehen so aus:



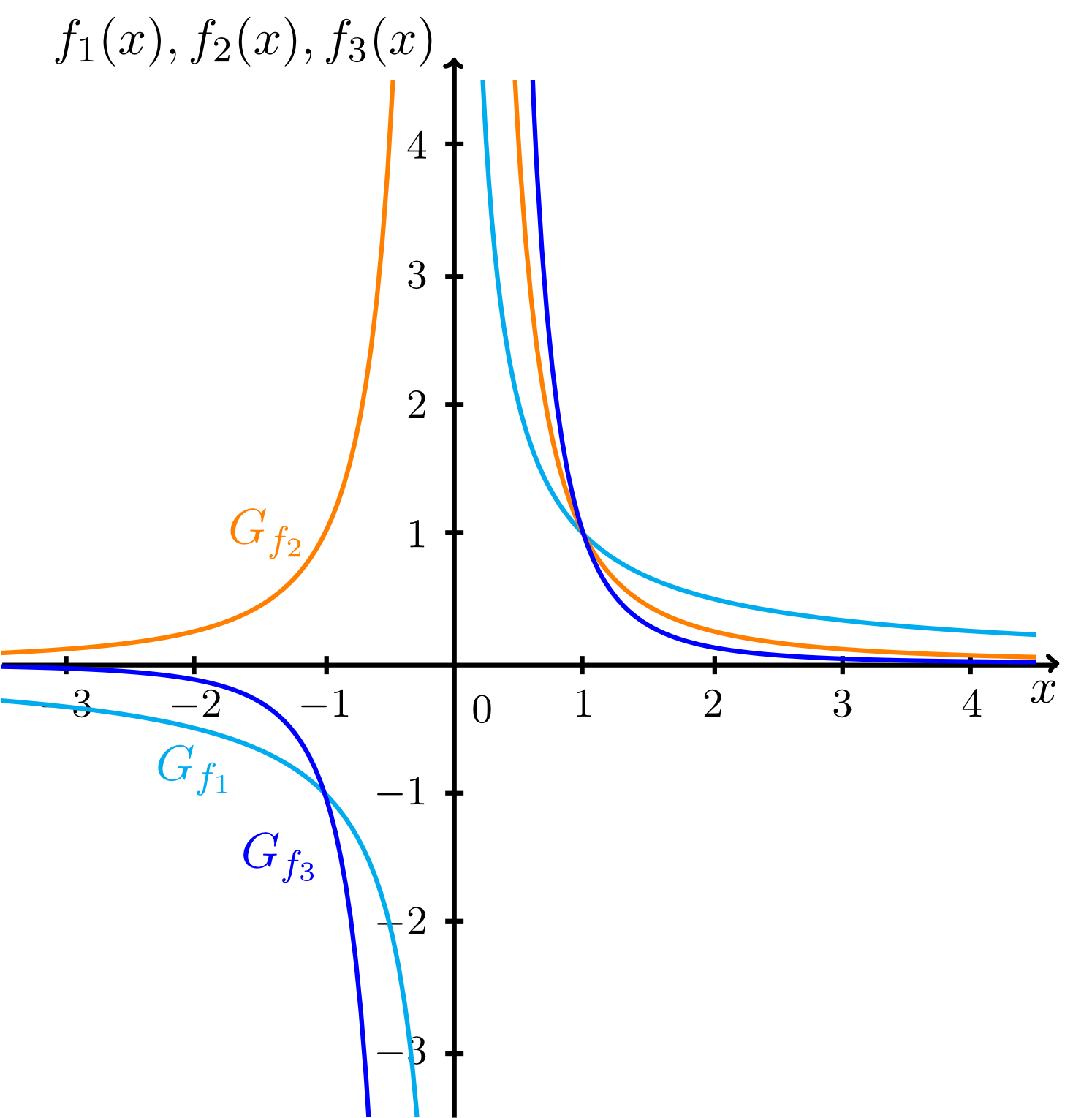
Insbesondere der Graph der Funktion

${\displaystyle f_1:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x}\hspace{0.5em},\hfill \end{array}}$
wird als Hyperbel bezeichnet.

Allgemein kann man für den Kehrwert eines beliebigen Monoms vom Grad $n\in \mathbb{N}$ also eine entsprechende Funktion hyperbolischen Typs angeben:



${\displaystyle f_n:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{0\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{1}{x^n}\hspace{0.5em}.\hfill \end{array}}$


Weitere Beispiele für Funktionen vom hyperbolischen Typ haben wir bereits in Beispiel 6.1.12 und Aufgabe 6.1.13 in Abschnitt 6.1.3 betrachtet.