Kapitel 6 Elementare Funktionen - Abschnitt 6.2 Lineare Funktionen und Polynome

6.2.6 Monome

Neben den linear-affinen Funktionen aus dem vorigen Abschnitt kann man sich nun auch Funktionen überlegen, die allen reellen Zahlen natürliche Potenzen ihrer selbst zuordnen. So zum Beispiel

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & x^2\hspace{0.5em}.\hfill \end{array}}$


       

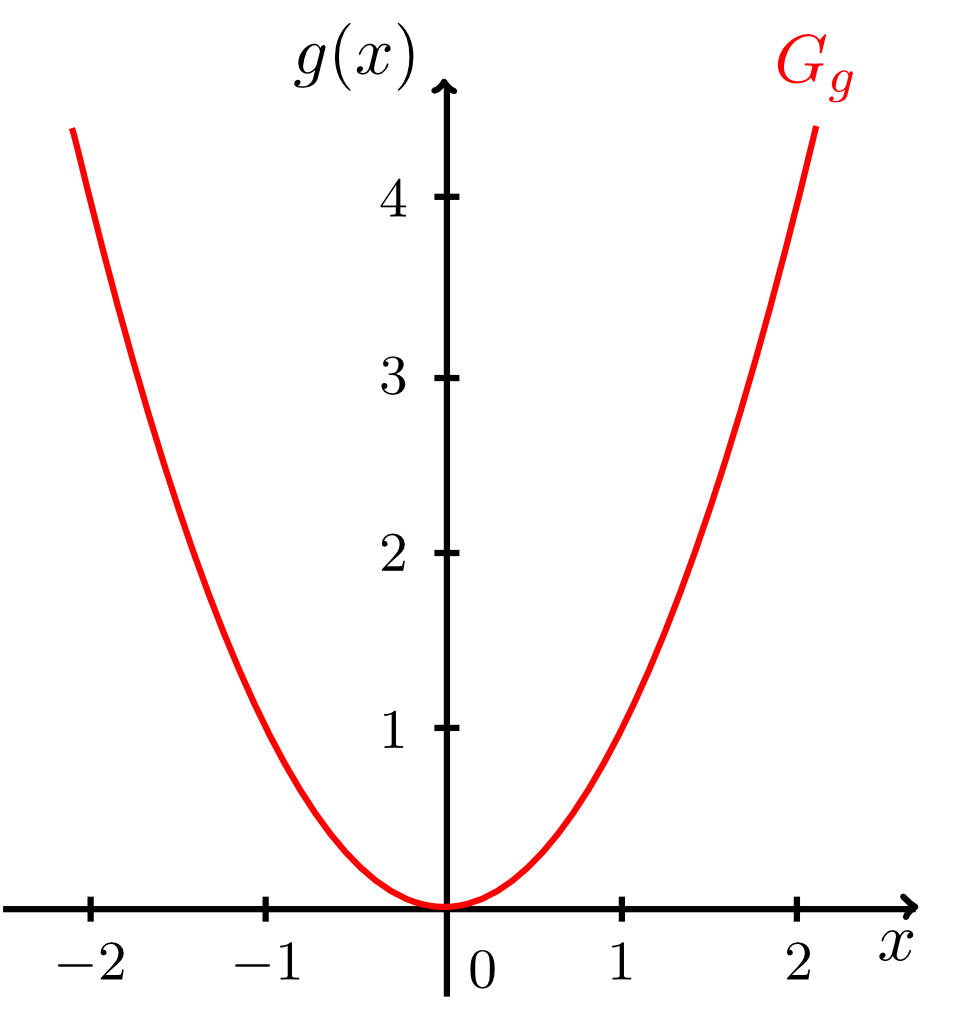
Dies funktioniert für jeden natürlichen Exponenten und man schreibt dann allgemein

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & x^n\hfill \end{array}}$
mit $n\in \mathbb{N}{}_0$ und bezeichnet diese Funktionen als Monome. Der Exponent $n$ eines Monoms wird als Grad des Monoms bezeichnet. So ist etwa die Funktion $g$ vom Anfang dieses Abschnitts ein Monom vom Grad $2$, usw.



Man bezeichnet das Monom vom Grad $2$ auch als die Standardparabel. Das Monom vom Grad $3$ wird auch als kubische Standardparabel bezeichnet. Hier einige Graphen von Monomen:



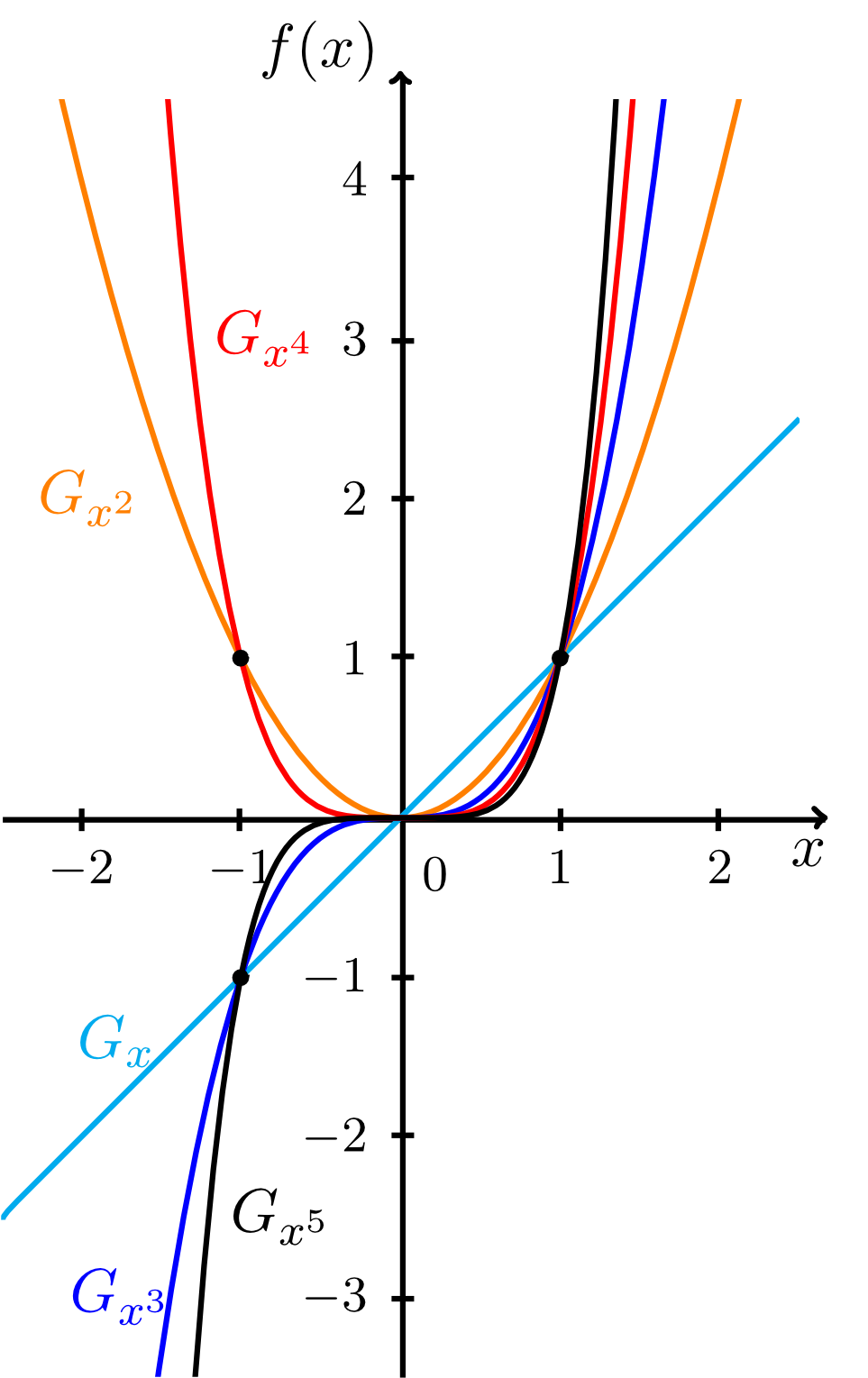
Auf Basis dieser Graphen fassen wir nun einige Erkenntisse über Monome zusammen: Es gibt einen grundlegenden Unterschied zwischen Monomen (mit Abbildungsvorschrift $f(x)=x^n$, $n\in \mathbb{N}$) von geradem und von ungeradem Grad. Die Monome von geradem Grad größer Null haben als Wertebereich immer die Menge $[0;\infty )$, während die Monome von ungeradem Grad ganz $ℝ$ als Wertebereich besitzen. Weiterhin gilt stets

${\displaystyle f(1)=1^n=1\hspace{0.5em},}$


${\displaystyle f(0)=0^n=0}$
und

${\displaystyle f(-1)=\{\begin{array}{cc}\hfill 1& \text{falls}\hspace{0.5em}n\hspace{0.5em}\text{gerade}\hfill \\ \hfill -1& \text{falls}\hspace{0.5em}n\hspace{0.5em}\text{ungerade .}\hfill \end{array}}$
Ferner gilt

${\displaystyle \{\begin{array}{cc}\hfill x>x^2>x^3>x^4>\dots & \text{für}\hspace{0.5em}x\in (0;1)\hfill \\ \hfill x<x^2<x^3<x^4<\dots & \text{für}\hspace{0.5em}x\in (1;\infty )\hspace{0.5em}.\hfill \end{array}}$