Kapitel 6 Elementare Funktionen - Abschnitt 6.7 Abschlusstest
6.7.1 Abschlusstest zu Modul 6
Dies ist ein einreichbarer Test:- Im Gegensatz zu den offenen Aufgaben werden beim Eingeben keine Hinweise zur Formulierung der mathematischen Ausdrücke gegeben.
- Der Test kann jederzeit neu gestartet oder verlassen werden.
- Der Test kann durch die Buttons am Ende der Seite beendet und abgeschickt, oder zurückgesetzt werden.
- Der Test kann mehrfach probiert werden. Für die Statistik zählt die zuletzt abgeschickte Version.
Aufgabe 6.7.1
Bestimmen Sie für die beiden Funktionen
und
jeweils den größtmöglichen Definitionsbereich bzw. .
Bestimmen Sie für die beiden Funktionen
und
jeweils den größtmöglichen Definitionsbereich bzw. .
Aufgabe 6.7.2
Bestimmen Sie für die Funktion
die Wertemenge .
Bestimmen Sie für die Funktion
die Wertemenge .
Aufgabe 6.7.3
Bestimmen Sie in der Exponentialfunktion
die Parameter , so dass und gilt.
Antwort: ,
,  .
.
Einfache Logarithmen können Sie stehen lassen, z.B. kann als ln(100) eingegeben werden auch wenn der exakte Wert von nicht bekannt ist.
Bestimmen Sie in der Exponentialfunktion
die Parameter , so dass und gilt.
Antwort:
Einfache Logarithmen können Sie stehen lassen, z.B. kann als ln(100) eingegeben werden auch wenn der exakte Wert von nicht bekannt ist.
Aufgabe 6.7.4
Bestimmen Sie die Verkettung (Erläuterung: ) der Funktionen
und
Antwort: .
.
Bestimmem Sie die Parameter, so dass die durch beschriebene Sinusschwingung diesen Graph besitzt:
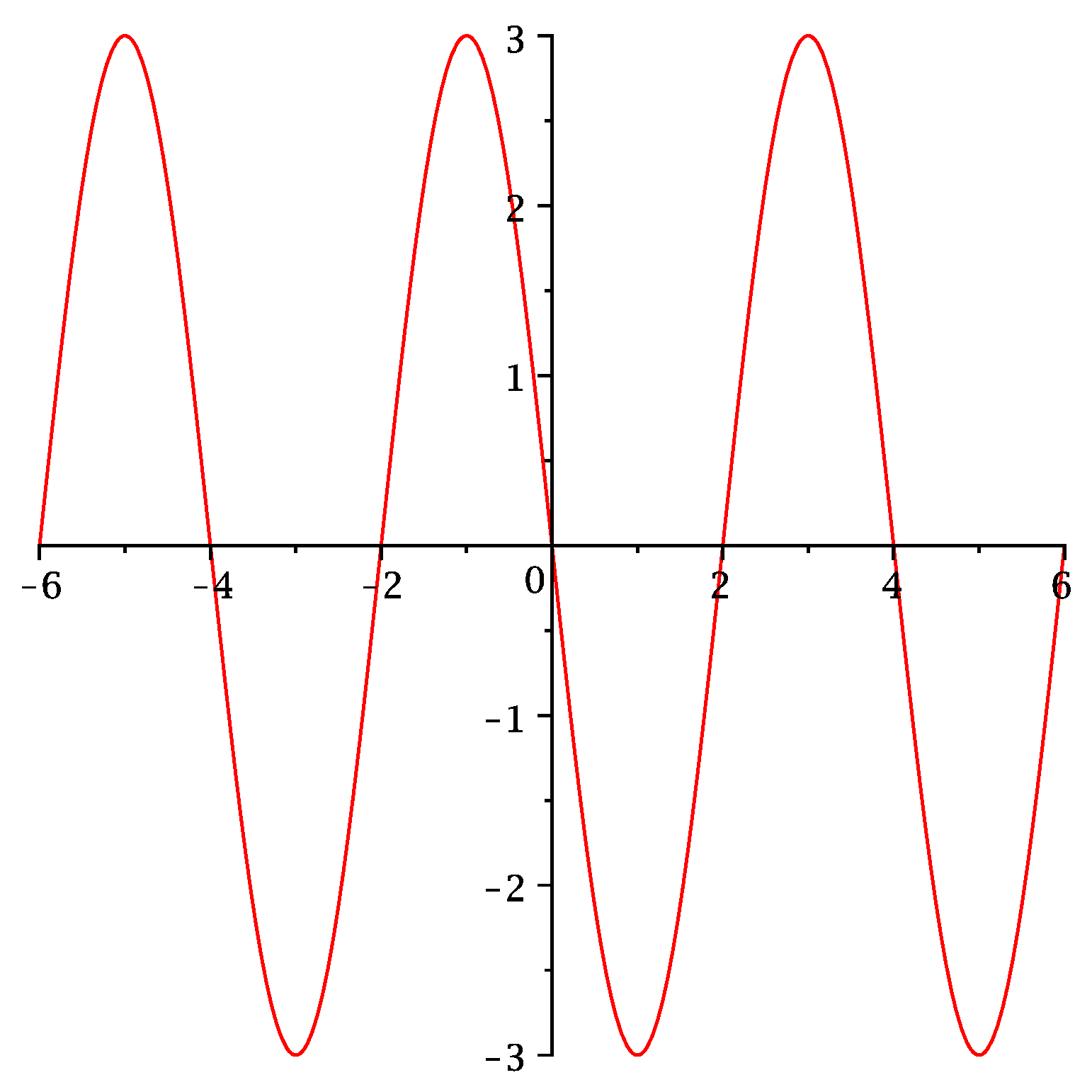
Antwort: .
.
Bestimmen Sie die Verkettung (Erläuterung: ) der Funktionen
und
Antwort:
Bestimmem Sie die Parameter, so dass die durch beschriebene Sinusschwingung diesen Graph besitzt:

Abbildung 1: Eine Sinusschwingung.
Antwort:
Aufgabe 6.7.5
Bestimmen Sie die Umkehrfunktion von
Die Funktion besitzt:
Bestimmen Sie die Umkehrfunktion von
Die Funktion besitzt:
- Den Definitionsbereich
 .
.
- Den Wertebereich
 .
.
- Die Funktionsvorschrift
 .
.
Aufgabe 6.7.6
Kreuzen Sie an, ob die Aussagen wahr oder falsch sind:
Die Funktion
Kreuzen Sie an, ob die Aussagen wahr oder falsch sind:
Die Funktion
|
| ... kann man kürzer auch als schreiben. | |
|
| ... ist eine linear-affine Funktion. | |
|
| ... hat die Wertemenge . | |
|
| ... hat die Steigung . | |
|
| ... kann nur Werte größer oder gleich und kleiner annehmen. | |
|
| ... hat als Graph ein Stück einer Gerade. | |
|
| ... hat bei den Wert . | |
|
| ... hat die Definitionsmenge . |
Aufgabe 6.7.7
Bestimmen Sie diese Logarithmen:
Bestimmen Sie diese Logarithmen:
 .
.
 .
.
 .
.
Hier erscheint die Testauswertung!

