Beispiel 6.4.1  
Eine Bakterienkultur enthält zu Versuchsbeginn $500$ Bakterien und verdoppelt ihre Population alle $13$ Minuten. Wir möchten gerne wissen, wieviele Bakterien nach $1$ Stunde und $15$ Minuten (also nach $75$ Minuten) in der Kultur vorhanden sind?

In einem ersten Anlauf können wir eine einfache Wertetabelle erstellen, die uns die Bakterienpopulation zu Beginn ($t=0$ min), nach $t=13$ min, nach $t=26$ min usw., also zu Vielfachen der $13$-Minuten-Verdopplungszeitspanne, angibt: Aus der Tabelle können wir abschätzen, dass die Antwort auf unsere Frage zwischen $16000$ und $32000$, wahrscheinlich näher bei $32000$, liegen wird. Doch wie sieht es mit einer präzis(er)en Antwort aus? Dazu müssen wir den funktionalen Zusammenhang zwischen allgemeinen $t$-Werten und Bakterienanzahl kennen. In der unten stehenden Abbildung ist auch der Graph einer Funktion $p$ wiedergegeben; dieser Funktionsgraph füllt sozusagen die Lücken zwischen den isolierten Punkten, die den Wertepaaren aus der Tabelle entsprechen und die ebenfalls eingezeichnet sind. Die zugehörige Abbildungsvorschrift ordnet jedem reellen Zeitpunkt eine Populationsgröße zu. Wie wir sehen werden, handelt es sich bei der Funktion um eine Exponentialfunktion. 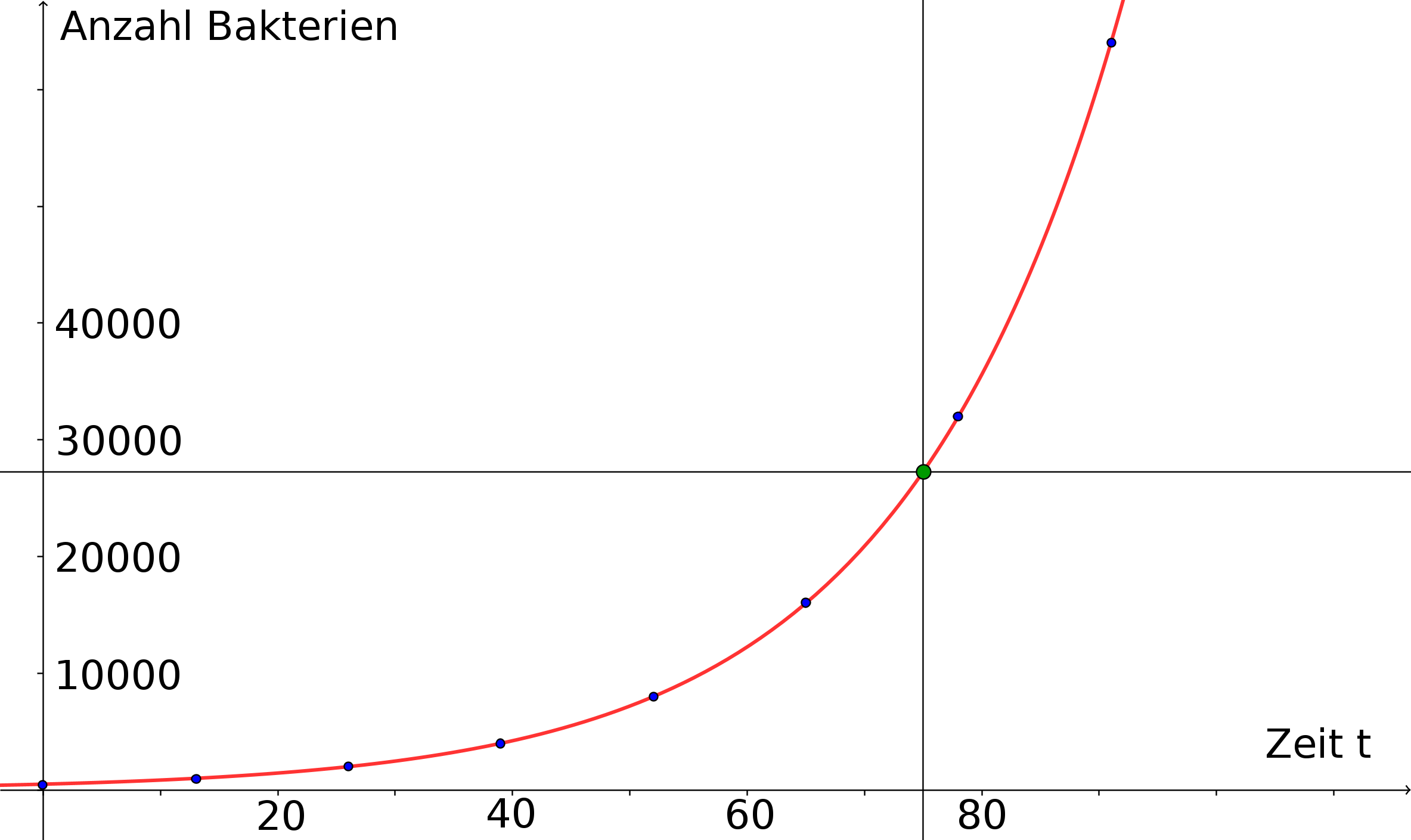Aus der graphischen Darstellung können wir die gesuchte Anzahl an Bakterien schon etwas genauer ablesen. Aber für die exakte Angabe benötigen wir die Abbildungsvorschrift, die hinter dem Graphen aus der Abbildung steht und die wir hier zunächst nur angeben:

${\displaystyle p:[0;\infty )\to (0;\infty )\mathrm{\hspace{0.5em}\hspace{0.5em}}\text{mit}\mathrm{\hspace{0.5em}\hspace{0.5em}}t⟼p(t)=500·2^{(t/13)}\hspace{0.5em}.}$

(In Aufgabe 6.4.3 werden wir diesen funktionalen Zusammenhang begründen.)
Damit erhalten wir für $t=75$ (gemessen in Minuten) den Funktionswert

${\displaystyle p(75)=500·2^{(75/13)}\approx 500·\mathrm{54,539545}\approx 27270\hspace{0.5em}.}$

Also leben nach $75$ Minuten $27270$ Bakterien in der fraglichen Population.