Onlinebrückenkurs Mathematik Abschnitt 5.1.3 Strahlensätze

Kapitel 5 Geometrie - Abschnitt 5.1 Grundbegriffe der ebenen Geometrie

5.1.3 Strahlensätze

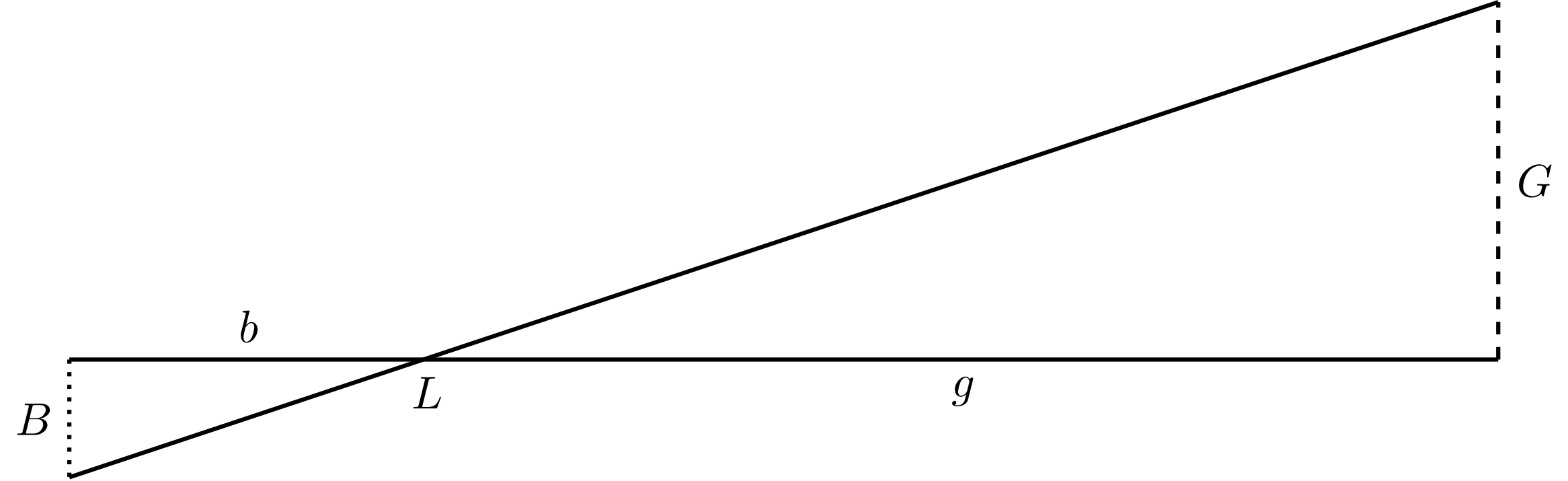
Eine Lochkamera liefert ein kleines Bild der Umwelt. Die Größenverhältnisse vom Bild

B

zum Gegenstand

G

sind proportional zu den Abständen

b

beziehungsweise

g

, die jeweils von der Lochblende

L

gemessen werden:

\frac{B}{G} = \frac{b}{g} .

Eigenschaften von Bildern einer zentrischen Streckung kann man ebenfalls mit den Strahlensätzen beschreiben (siehe auch die Abbildung 5.3.17).

Die gemeinsame Eigenschaft der Beispiele findet sich darin, dass Strahlen (oder Geraden) mit einem gemeinsamen Schnittpunkt von parallelen Geraden geschnitten werden.

Strahlensätze 5.1.4
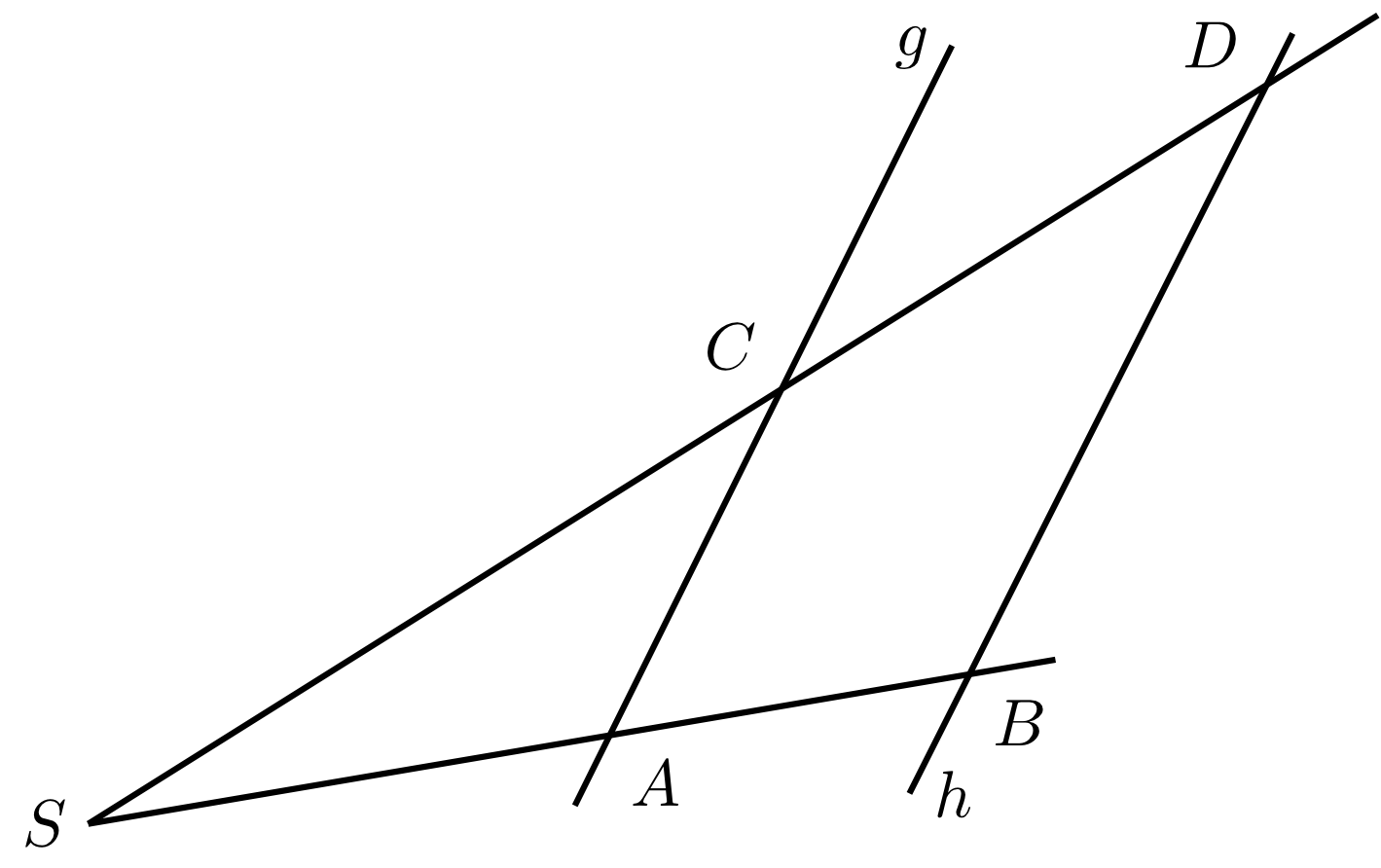
Vom gemeinsamen Punkt

S

gehen zwei Strahlen

s_{1}

und

s_{2}

aus, die durch die Punkte

A

beziehungsweise

C

verlaufen. Der Punkt

B

liegt auf dem Strahl

s_{1}

und

D

liegt auf dem Strahl

s_{2}

. Zuerst werden die Strecken zwischen den Punkten auf den beiden Strahlen betrachtet, dann auch zwischen den Strahlen.

Für zwei Punkte

P

und

Q

sei

\overline{P Q}

die Strecke von

P

nach

Q

, und

[\overline{P Q}]

bezeichne die Länge dieser Strecke.

Wenn die Geraden

g

und

h

parallel sind, gelten die folgenden Aussagen:

Die Abschnitte auf einem Strahl verhalten sich wie die entsprechenden Abschnitte auf dem anderen Strahl:

$\frac{[\overline{S A}]}{[\overline{S C}]} = \frac{[\overline{A B}]}{[\overline{C D}]} = \frac{[\overline{S B}]}{[\overline{S D}]} .$
Dies kann auch so ausgedrückt werden:

$\frac{[\overline{S A}]}{[\overline{A B}]} = \frac{[\overline{S C}]}{[\overline{C D}]} und \frac{[\overline{S A}]}{[\overline{S B}]} = \frac{[\overline{S C}]}{[\overline{S D}]} .$
Die Abschnitte auf den Parallelen verhalten sich wie die von $S$ ausgehenden entsprechenden Abschnitte auf einem Strahl:

$\frac{[\overline{S A}]}{[\overline{S B}]} = \frac{[\overline{A C}]}{[\overline{B D}]} = \frac{[\overline{S C}]}{[\overline{S D}]} .$
Dies kann auch so ausgedrückt werden:

$\frac{[\overline{S A}]}{[\overline{A C}]} = \frac{[\overline{S B}]}{[\overline{B D}]} und \frac{[\overline{S C}]}{[\overline{C A}]} = \frac{[\overline{S D}]}{[\overline{D B}]},$
wobei $[\overline{A C}] = [\overline{C A}]$ und $[\overline{B D}] = [\overline{D B}]$ gilt.

Die Aussagen der Strahlensätze gelten auch, wenn anstelle von Strahlen zwei Geraden betrachtet werden, die sich im Punkt

S

schneiden. Als Anwendungsbeispiel ist oben eine Lochkamera genannt worden.

Auf diese Weise können Entfernungen zwischen Punkten berechnet werden, ohne dass die Strecke direkt gemessen wird.

Beispiel 5.1.5
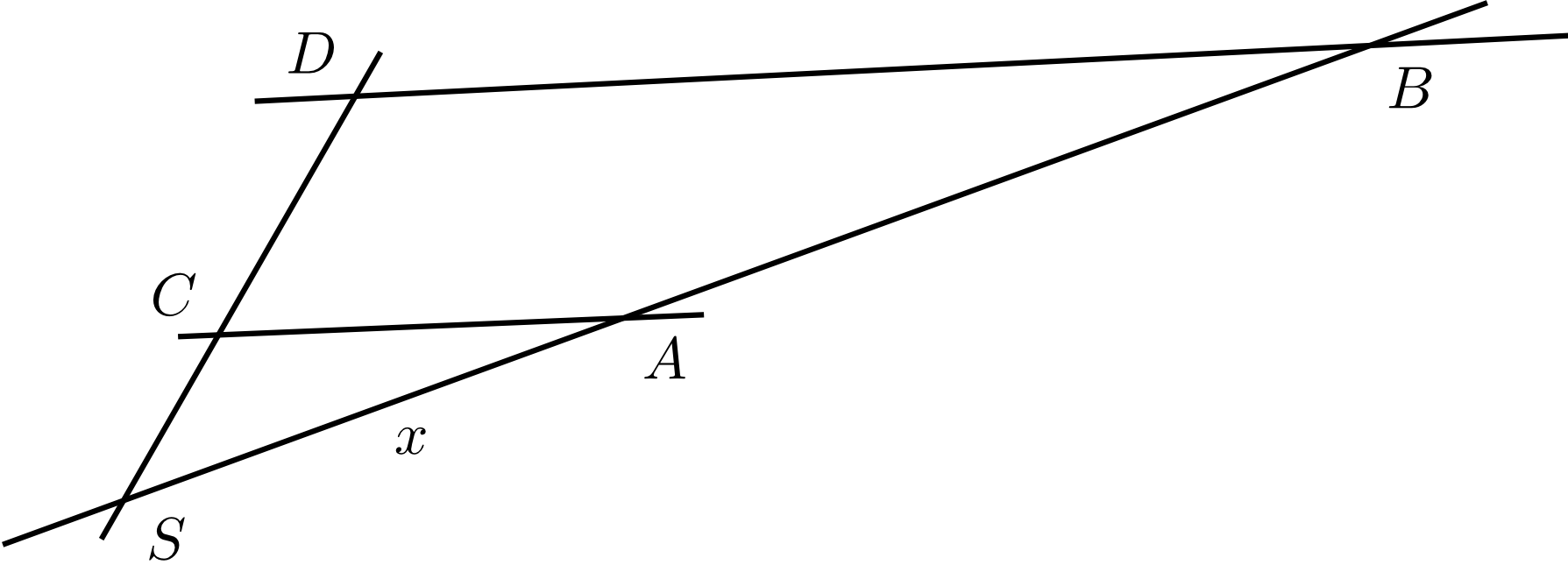
Die gegebenen Punkte

A

B

C

und

D

bestimmen die Geraden

A B

und

C D

, die sich im Punkt

S

schneiden. Weiter ist bekannt, dass die Geraden

A C

und

B D

parallel sind. Zwischen den Punkten wurden die Abstände

[\overline{A B}] = 51

[\overline{S C}] = 12

und

[\overline{C D}] = 18

gemessen.

Daraus wird berechnet, wie weit

A

von

S

entfernt ist. Wenn der gesuchte Abstand mit

x

bezeichnet wird, gilt mit den Strahlensätzen dann

\frac{x}{[\overline{A B}]} = \frac{[\overline{S C}]}{[\overline{C D}]},

woraus

x = \frac{[\overline{S C}]}{[\overline{C D}]} \cdot [\overline{A B}] = \frac{12}{18} \cdot 51 = \frac{2}{3} \cdot 51 = 34

folgt.