Onlinebrückenkurs Mathematik Abschnitt 5.3.4 Kongruente und ähnliche Dreiecke

Kapitel 5 Geometrie - Abschnitt 5.3 Rund um Dreiecke

5.3.4 Kongruente und ähnliche Dreiecke

Zu einem Dreieck gehören unter anderem drei Seitenlängen und drei Winkel. Die Außenwinkel sind durch die Innenwinkel bereits festgelegt, sodass durch diese sechs Größen die „Form“ eines Dreieck bestimmt ist. Wenn bei zwei Dreiecken alle diese Größen übereinstimmen, so sind diese Dreiecke deckungsgleich oder kongruent. Dabei spielt es keine Rolle, wo sich die Dreiecke befinden. Kongruente Dreiecke können also durch Drehung, Spiegelung und Verschiebung ineinander überführt werden.
Kennt man vier von den sechs Größen, so ist das Dreieck eindeutig bestimmt bis auf Spielgelung oder Drehung, das heißt bis auf die Lage des Dreiecks im Raum. Alle Dreiecke, die man mit diesen Angaben erhält, sind dann kongruent. In einigen Fällen genügen sogar drei Angaben, um das Dreieck eindeutig zu bestimmen. Sie werden in den Kongruenzsätzen beschrieben:

Kongruenzsätze für Dreiecke 5.3.13
Ein Dreieck ist bis auf seine Lage in der Ebene eindeutig bestimmt, wenn eine der folgenden Situationen vorliegt:

Von den drei Winkeln und den drei Seitenlängen sind mindestens vier Angaben gegeben.
Alle drei Seitenlängen sind gegeben. (Diesen Satz bezeichnet man gerne mit „sss“ für „Seite, Seite, Seite“.)
Eine Seitenlänge und ihre Winkel zu den anderen Seiten sind gegeben („wsw“ für „Winkel, Seite, Winkel“).
Zwei Seitenlängen und der von den Seiten eingeschlossene Winkel sind gegeben („sws“ für „Seite, Winkel, Seite“).
Ein Winkel und zwei Seitenlängen sind so gegeben, dass nur eine der Seiten auf einem Schenkel des Winkels liegt und die andere gegebene Seite die längere der beiden gegebenen Seiten ist.

(Diesen Satz bezeichnet man mit „Ssw“ für „Seite, Seite, Winkel“, wobei das groß geschriebene „S“ signalisieren soll, dass die dem Winkel gegenüberliegende Seite die längere Seite darstellt.)

Wenn von einem Dreieck nur zwei oder drei Angaben gegeben sind, die keinem der oben angegebenen Fälle entsprechen, so gibt es verschiedene Dreiecke, für die die Angaben zutreffen und die nicht deckungsgleich sind.

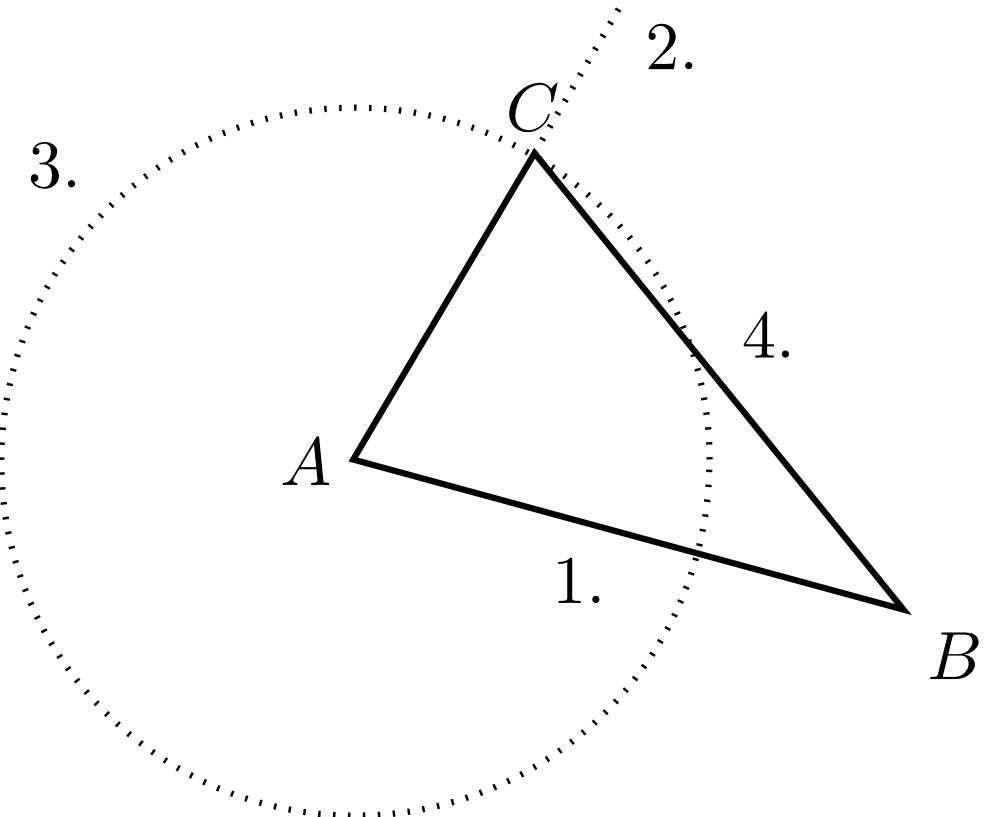
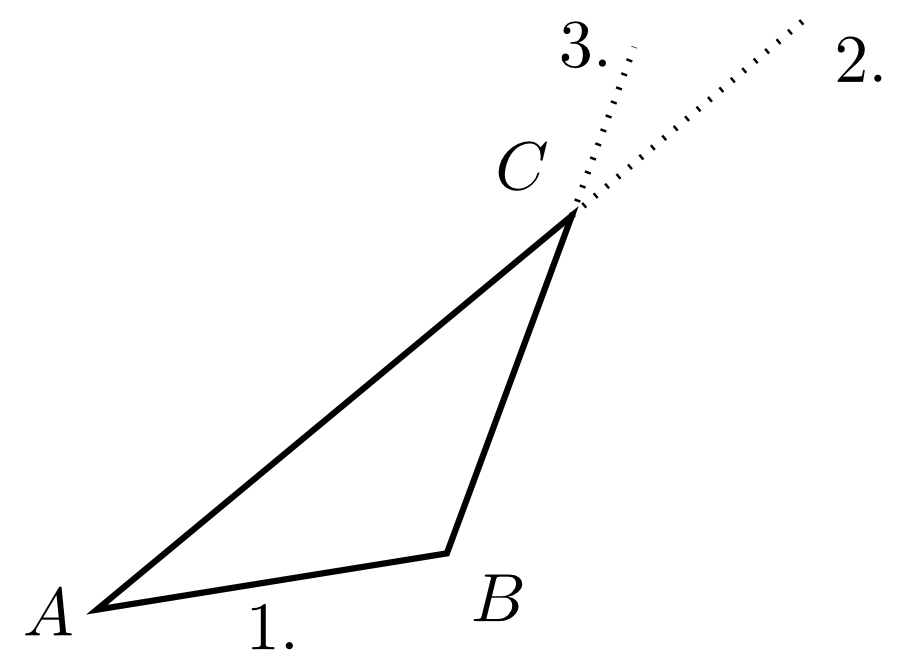
Im Folgenden wird zuerst in einen Beispiel erläutert, wie mit den Kongruenzsätzen ein Dreieck konstruiert werden kann. Danach wird ein Beispiel zu Dreiecken betrachtet, bei denen nur die Winkel gegeben sind und somit keine der obigen Bedingungen erfüllt ist.

Beispiel 5.3.14

Gegeben seien die Seiten

b

und

c

und der Winkel

α

. Das Dreieck „sws“ erhält man, indem man zunächst eine Seite, hier zum Beispiel die Seite

c

, zeichnet und an der nach der Bezeichnungskonvention passenden Ecke (

A

) den Winkel

α

anfügt. Dann schlägt man um diese Ecke einen Kreis, dessen Radius der Länge der zweiten Seite (hier

b

) entspricht. Der Schnittpunkt dieses Kreises mit dem zweiten Schenkel des Winkels bildet die dritte Ecke des Dreiecks (

C

Aufgabe 5.3.15
Konstruieren Sie ein Dreieck mit einer Seite

c = 5

und den Winkeln

α = 30^{\circ}

und

β = 120^{\circ}

, wobei die oben eingeführte Notation verwendet wird.

Man zeichnet zuerst die gegebene Strecke

c

. Dann trägt man an den beiden Enden der Strecke die zwei der Bezeichnungskonvention entsprechenden Winkel an. Der Schnittpunkt

C

der beiden neuen Schenkel ist die dritte Ecke des Dreiecks.

Beispiel 5.3.16
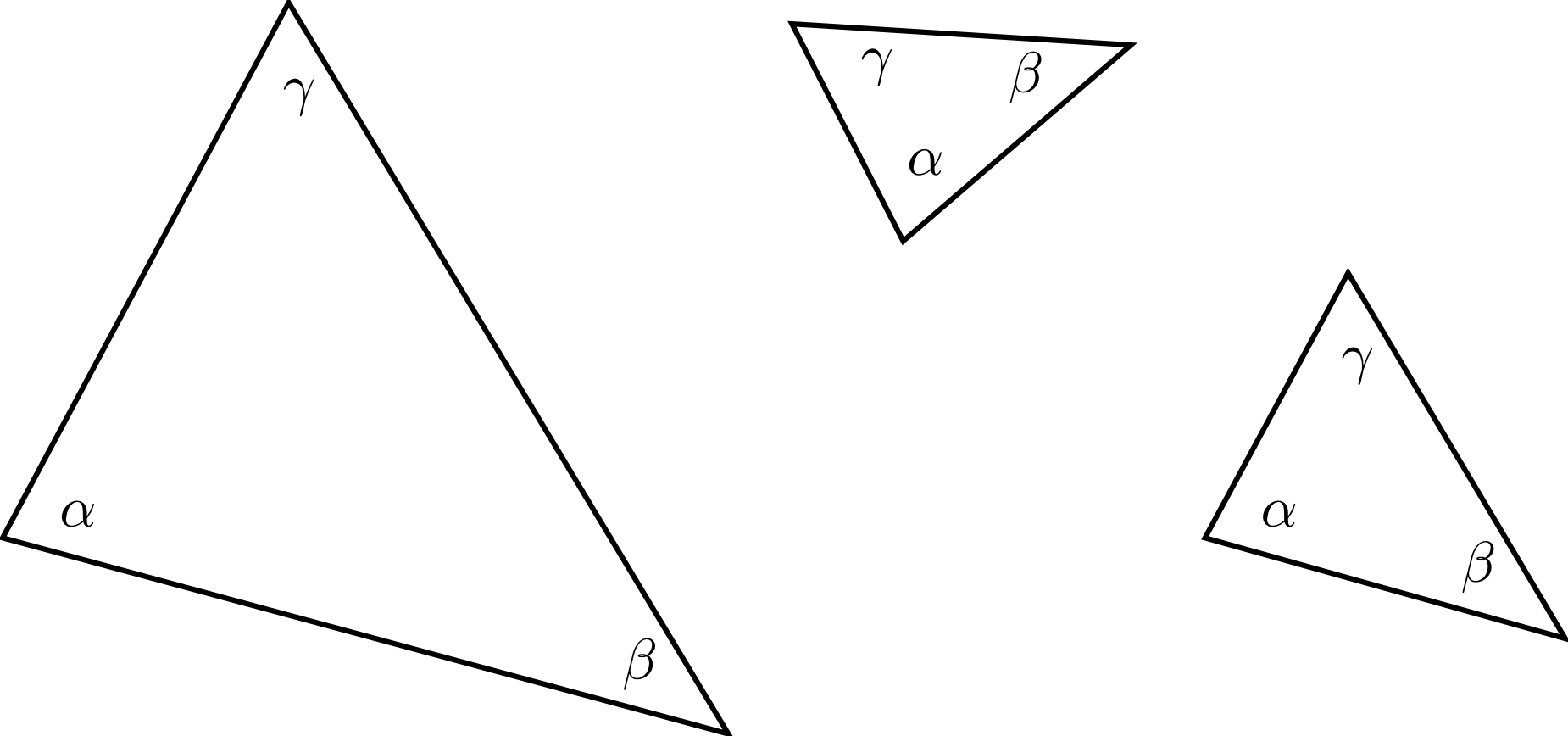
Gegeben seien nun die drei Winkel

α = 77^{\circ}

β = 44^{\circ}

und

γ = 59^{\circ}

, deren Summe

180^{\circ}

ist. Diese Auswahl von drei Winkeln ohne Angabe zu einer Seite findet man nicht bei den Kongruenzsätzen 5.3.13. Beispiele solcher Dreicke sind hier dargestellt:

Es gibt sogar unendlich viele derartige Dreiecke, die die angegebenen Winkel haben und die nicht kongruent zueinander sind, also nicht durch Drehung oder Spiegelung ineinander übergeführt werden können.

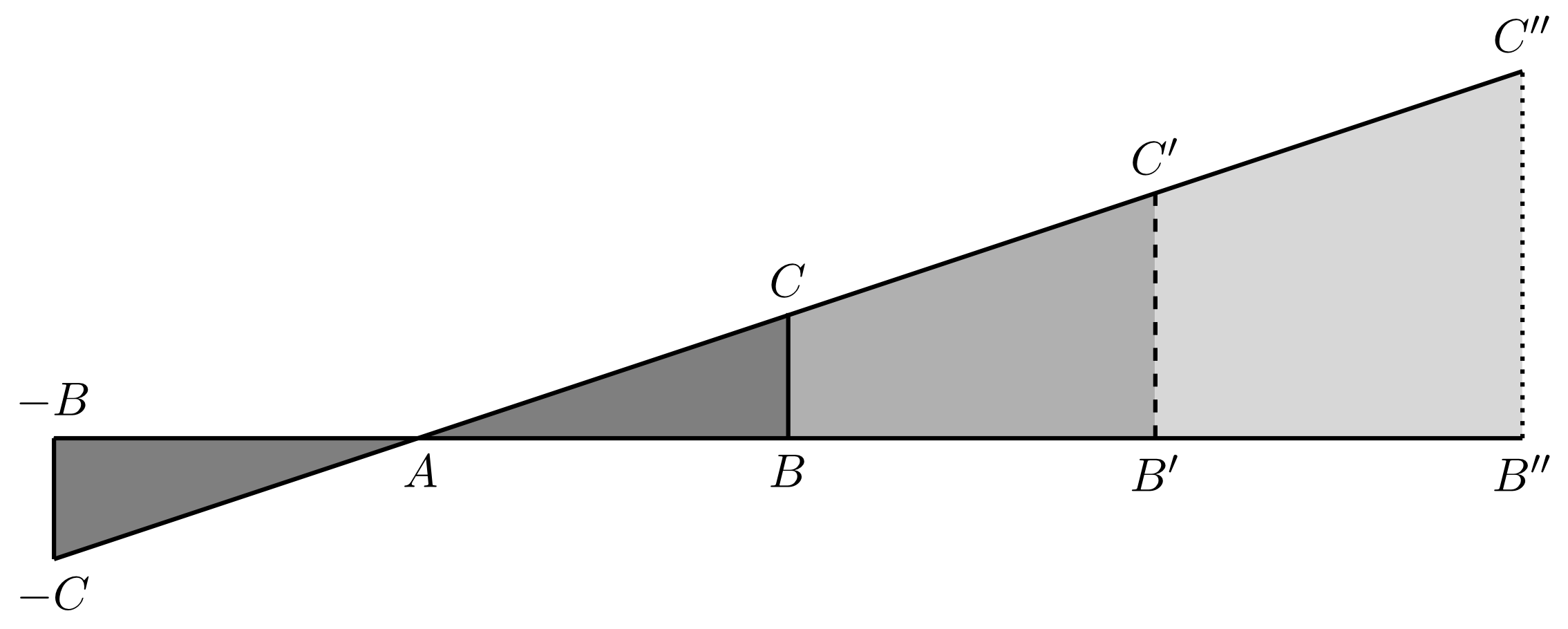
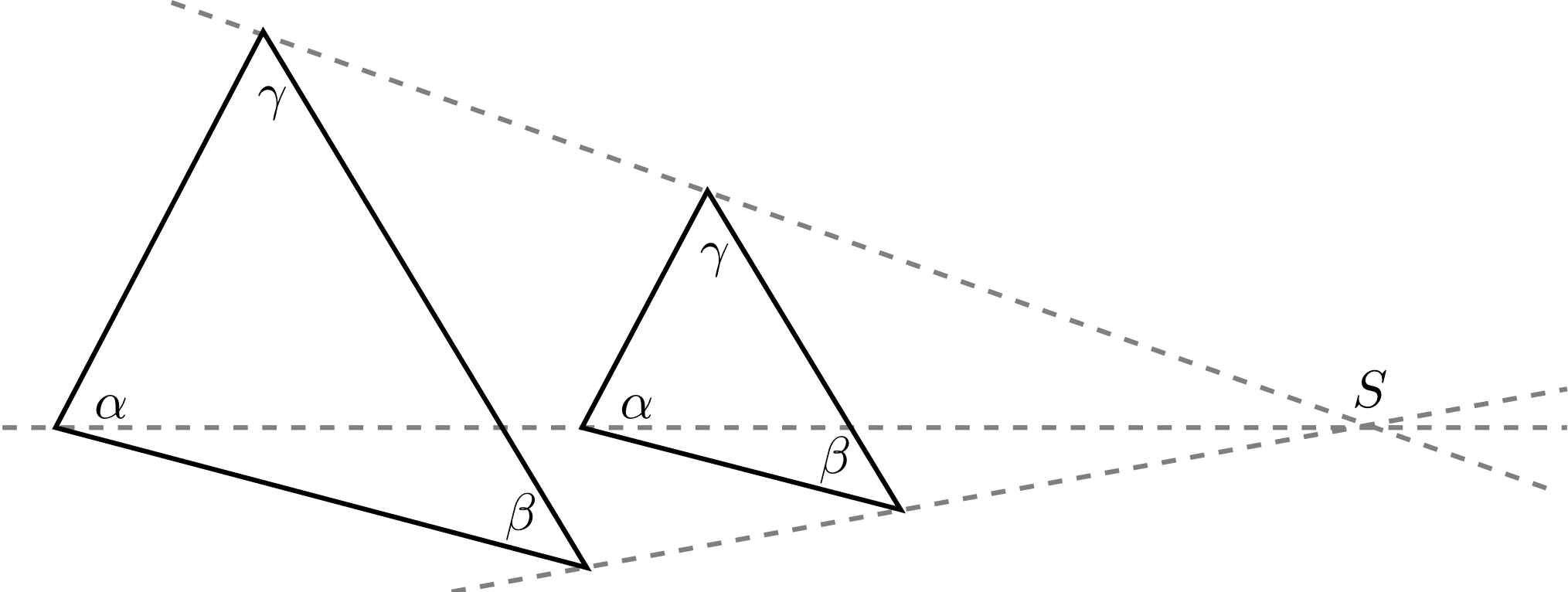
Allerdings sehen diese Dreiecke irgendwie ähnlich aus. Solche ähnlichen Dreiecke erhält man auch, wenn man zum Beispiel die Verhältnisse aller Seiten zueinander kennt. Dies ergibt sich aus den Strahlensätzen, wie die folgende Zeichnung verdeutlicht:

Ähnlichkeitssätze für Dreiecke 5.3.17
Zwei Dreiecke heißen zueinander ähnlich, wenn sie

in zwei (und damit wegen der Winkelinnensumme in drei) Winkeln übereinstimmen, oder
in allen Verhältnissen ihrer entsprechenden Seiten übereinstimmen, oder
in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen, oder
im Verhältnis zweier Seiten und im Gegenwinkel der größeren Seite übereinstimmen.

Eine Besonderheit gibt es bei dem rechten und dem linken Dreieck in Beispiel 5.3.16: Hier geht das eine Dreieck durch zentrische Streckung mit dem Streckzentrum

S

und einem Streckfaktor

k

in das andere über.