Onlinebrückenkurs Mathematik Abschnitt 5.3.3 Satz des Pythagoras

Kapitel 5 Geometrie - Abschnitt 5.3 Rund um Dreiecke

5.3.3 Satz des Pythagoras

Eine Aussage über die Seitenlängen in einem rechtwinkligen Dreieck bietet der Satz des Pythagoras. Dieser wird hier in einer oft verwendeten Formulierung angegeben.

Satz des Pythagoras 5.3.3

Es wird ein rechtwinkliges Dreieck betrachtet, in dem der rechte Winkel bei

C

liegt.

Dann ist die Summe der Quadrate über den Katheten

a

und

b

gleich dem Quadrat über der Hypotenuse

c

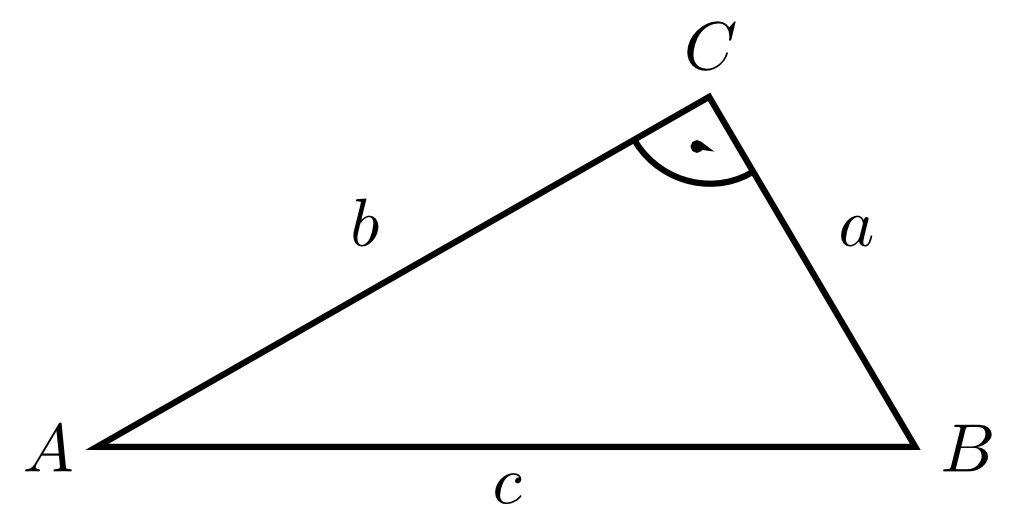
. Mit den genannten Bezeichnungen gilt somit (siehe auch das abgebildete Dreieck):

a^{2} + b^{2} = c^{2} .

Werden die Seiten des Dreiecks anders bezeichnet, muss die Gleichung entsprechend angepasst werden!

Beispiel 5.3.4
Gegeben sei ein rechtwinkliges Dreieck mit den Kathetenlängen

a = 6

und

b = 8

.

Die Länge der Hypotenuse kann mithilfe des Satzes von Pythagoras berechnet werden:

c = \sqrt{c^{2}} = \sqrt{a^{2} + b^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10 .

Aufgabe 5.3.5
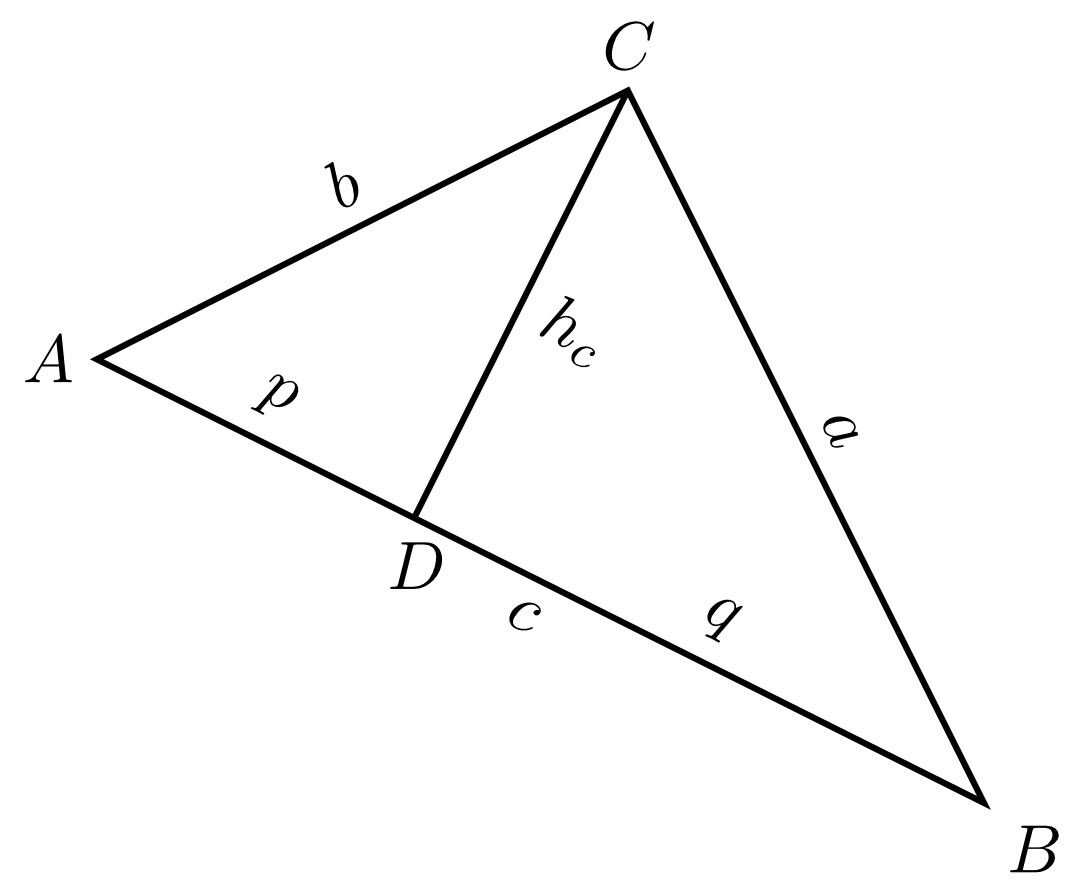
Gegeben ist ein rechtwinkliges Dreieck

A B C

mit rechtem Winkel in

C

, der Hypotenuse

c = \frac{25}{3}

und der Höhe

h_{c} = 4

sowie der Strecke

\overline{D B}

mit

q = [\overline{D B}] = 3

. Dabei bezeichnet

D

den Höhenfußpunkt der Höhe

h_{c}

. Berechnen Sie die Länge der beiden Katheten

a

und

b

Es wird der Satz des Pythagoras auf das Dreieck

D B C

angewandt, das in

D

einen rechten Winkel hat. Dann ist

a = \sqrt{h_{c}^{2} + q^{2}} = \sqrt{4^{2} + 3^{2}} = \sqrt{25} = 5 .

Nun wird der Satz des Pythagoras auf das gegebene rechtwinklige Dreieck

A B C

angewandt, woraus

b = \sqrt{c^{2} - a^{2}} = \sqrt{{(\frac{25}{3})}^{2} - 5^{2}} = \sqrt{\frac{400}{9}} = \frac{20}{3}

folgt.

Der Satz des Thales ist ein weiterer wichtiger Satz, der eine Aussage über rechtwinklige Dreiecke ausdrückt.

Satz des Thales 5.3.6

Hat das Dreieck

A B C

bei

C

einen rechten Winkel, so liegt

C

auf einem Kreis mit Radius

r

und der Hypotenuse

\overline{A B}

als Durchmesser der Länge

2 r

Die umgekehrte Aussage gilt ebenso. Wenn man über einer Strecke

\overline{A B}

einen Halbkreis konstruiert und dann

A

und

B

mit einem beliebigen Punkt

C

auf dem Halbkreis verbindet, dann ist das so entstandene Dreieck immer rechtwinklig.

Beispiel 5.3.7
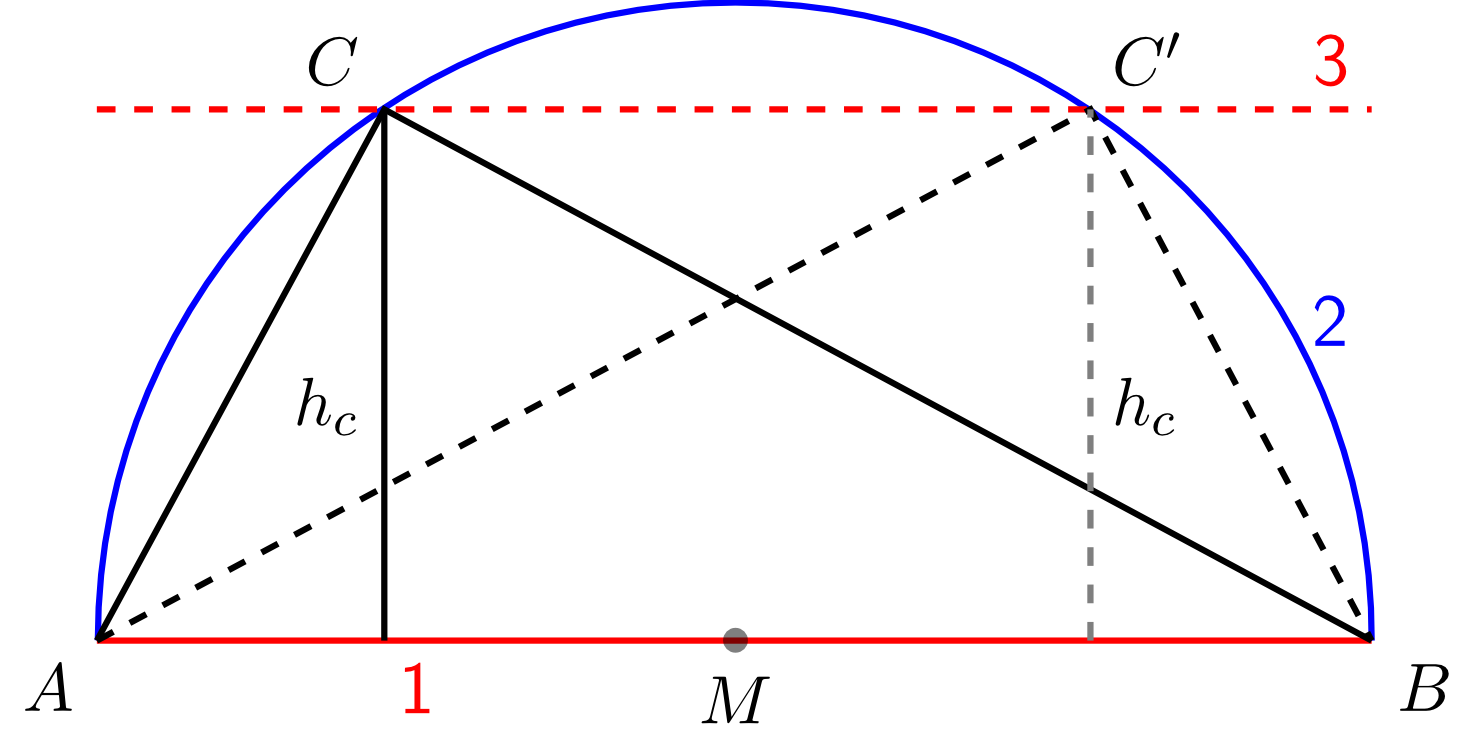
Es soll ein rechtwinkliges Dreieck mit der Hypotenusenlänge

c = 6 cm

und der Höhe

h_{c} = 2,5 cm

konstruiert werden.

Zuerst zeichnet man die Hypotenuse

$c = \overline{A B} .$
Die Mitte der Hypotenuse wird nun zum Mittelpunkt eines Kreises mit dem Radius $r = c / 2$ .
Nun zeichnet man eine Parallele zur Hypotenuse im Abstand $h_{c}$ . Es gibt zwei Schnittpunkte $C$ und $C'$ dieser Parallelen mit dem Thaleskreis.

Diese Schnittpunkte sind jeweils die dritte Ecke eines Dreiecks, das die geforderten Eigenschaften hat, das heißt, man erhält zwei Lösungen. Würde man noch einen Thaleskreis nach unten zeichen, so ergäben sich noch mal zwei Lösungen. Wenn es nicht um die Lage, sondern nur um die „Form“ der Dreiecke geht, dann sind alle diese Dreiecke „deckungsgleich“ (siehe auch 5.3.13).

Aufgabe 5.3.8
Welche Höhe

h_{c}

kann ein rechtwinkliges Dreieck mit der Hypotenuse

c

maximal haben?

Die Höhe

h_{c}

kann maximal so groß werden wie der Radius des Thaleskreises über der Hypotenuse. Es ist also

h_{c} \leq \frac{c}{2}

Diese Inhalte liegen über dem Kursniveau und werden in den Aufgaben und Tests nicht abgefragt.

In einem rechtwinkligen Dreieck gelten neben dem Satz des Pythagoras weitere Aussagen. Dazu werden folgende Bezeichnungen verwendet:

Es wird ein rechtwinkliges Dreieck mit rechtem Winkel bei

C

betrachtet. Die Höhe

h_{c}

schneidet die Hypotenuse des Dreiecks

A B C

im Punkt

D

, dem Höhenfußpunkt. Weiter werden die Bezeichnungen

p = [\overline{A D}]

und

q = [\overline{B D}]

vereinbart.

Höhensatz 5.3.9
Das Quadrat über der Höhe ist flächeninhaltsgleich dem Rechteck aus den beiden Hypotenusenabschnitten:

h^{2} = p \cdot q .

Kathetensatz 5.3.10
Das Quadrat über einer Kathete ist flächeninhaltsgleich dem Rechteck aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt:

a^{2} = c \cdot q, b^{2} = c \cdot p .

Beispiel 5.3.11
Gegeben sei ein rechtwinkliges Dreieck mit den Kathetenlängen

a = 3

und

b = 4

.

Die Länge der Hypotenuse kann mithilfe des Satzes von Pythagoras berechnet werden:

c = \sqrt{a^{2} + b^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5 .

Die einzelnen Hypotenusenabschnitte

p

und

q

berechnen sich gemäß dem Kathetensatz zu:

q = \frac{a^{2}}{c} = \frac{9}{5} = 1,8 und p = \frac{b^{2}}{c} = \frac{16}{5} = 3,2 .

Die Höhe

h_{c}

erhält man mit dem Höhensatz:

h_{c} = \sqrt{p \cdot q} = \sqrt{\frac{9}{5} \cdot \frac{16}{5}} = \sqrt{\frac{144}{25}} = \frac{12}{5} = 2,4 .

Aufgabe 5.3.12
Berechnen Sie für ein rechtwinkliges Dreieck mit der Hypotenuse

c = 10,5

, der Höhe

h_{c} = 5,04

und dem Hypotenusenabschnitt

q = 3,78

die Länge der beiden Katheten.

Kathetensatz: a = \sqrt{c \cdot q} = \sqrt{10,5 \cdot 3,78} = 6,3;

Satz des Pythagoras: b = \sqrt{c^{2} - a^{2}} = \sqrt{{10,5}^{2} - {6,3}^{2}} = 8,4 .