Kapitel 5 Geometrie - Abschnitt 5.4 Vielecke, Flächeninhalt und Umfang
5.4.2 Vierecke
Im vorherigen Abschnitt 5.3 wurden Dreiecke betrachtet. Dazu wurde von drei Punkten ausgegangen, die nicht auf einer Geraden liegen. Verbindet man drei solche Punkte durch alle möglichen Strecken zwischen zwei der drei Punkte, ergibt sich immer ein geschlossener Weg, in dem jeder gegebene Punkt genau zwei Strecken verbindet. Dabei haben die Strecken nur ihre Endpunkte mit anderen Strecken gemeinsam. Außerdem gibt es keine Kreuzungspunkte.
Bei mehr als drei Punkten ist dies nicht immer der Fall. Bereits vier Punkte können so verbunden werden, dass sich die Verbindungsstrecken kreuzen oder dass sich mehrere geschlossene Wege ergeben.
Hier sollen die Strecken alle gegebenen Punkte durch einen einzigen geschlossenen Weg miteinander verbinden, der kreuzungsfrei verläuft.
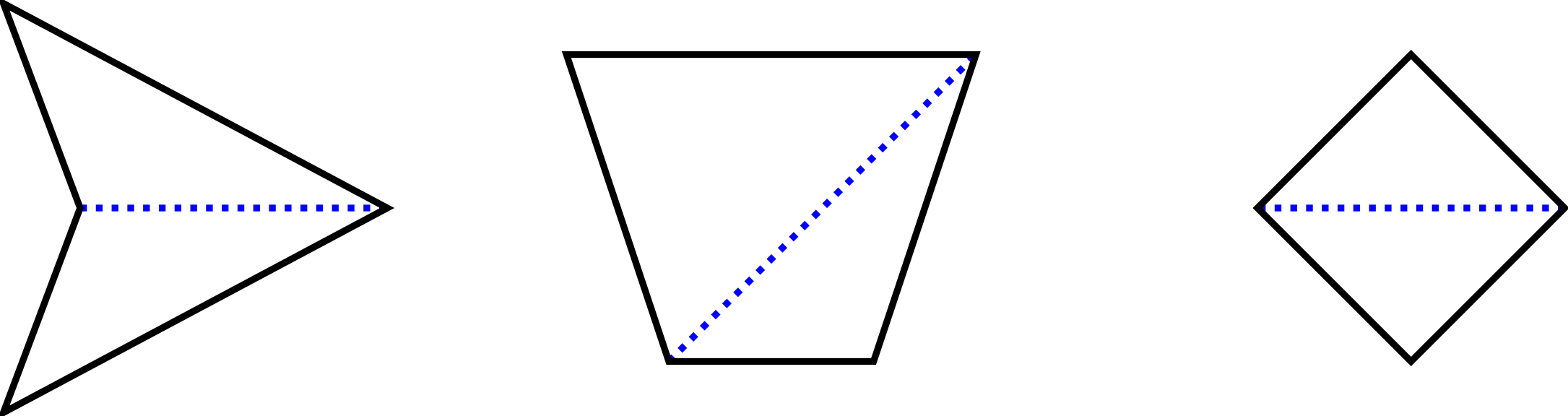
Offenbar kann ein Viereck in zwei Dreiecke zerlegt werden. Im Allgemeinen erhält man die beiden Dreiecke, wenn man eine Ecke mit dem größten Winkel mit der gegenüberliegenden Ecke durch eine Strecke verbindet. Eine solche Strecke zwischen Ecken, die nicht miteinander verbunden sind, heißt eine Diagonale des Vierecks. Aus der Kenntnis, dass die Summe der (Innen-)Winkel eines Dreicks beziehungsweise ist, folgt damit, dass die Summe der (Innen-)Winkel eines Vierecks doppelt so groß ist, also beziehungsweise beträgt.
Vierecke
5.4.1
Es werden Vierecke betrachtet, die sich dadurch ergeben, dass vier gegebene Punkte so durch Strecken miteinander werden, dass ein einziger geschlossener, kreuzungsfreier Weg durch alle vier Punkte entsteht. Dabei sollen je drei der gegebenen Punkte, die durch zwei Strecken miteinander verbunden sind, nicht auf einer Geraden liegen.
Wie bei Dreiecken werden auch bei Vierecken die Innenwinkel kurz als Winkel bezeichnet, wenn in einem besonderen Kontext nichts anderes vermerkt wird.
Es werden Vierecke betrachtet, die sich dadurch ergeben, dass vier gegebene Punkte so durch Strecken miteinander werden, dass ein einziger geschlossener, kreuzungsfreier Weg durch alle vier Punkte entsteht. Dabei sollen je drei der gegebenen Punkte, die durch zwei Strecken miteinander verbunden sind, nicht auf einer Geraden liegen.
Wie bei Dreiecken werden auch bei Vierecken die Innenwinkel kurz als Winkel bezeichnet, wenn in einem besonderen Kontext nichts anderes vermerkt wird.
Ebenso wie bei Dreiecken wird auch die Idee zu Vierecken in vielfältiger Weise in technischen Konstruktionen verwendet. Dadurch sind weitere alltägliche Namen gebräuchlich, die verschiedene Klassen von Vierecken bezeichnen.
Wie bei Dreiecken werden auch Vierecke nach der Länge von Seiten oder nach der Größe von Winkeln eingeteilt. Dabei erkennt man typische Unterschiede zu Dreiecken. Anders als dort kann es bei Vierecken beispielsweise parallele Seiten geben. Außerdem ist es möglich, dass es mehr als eine Ecke mit einem rechten Winkel gibt.
Besondere Klassen von Vierecken
5.4.2
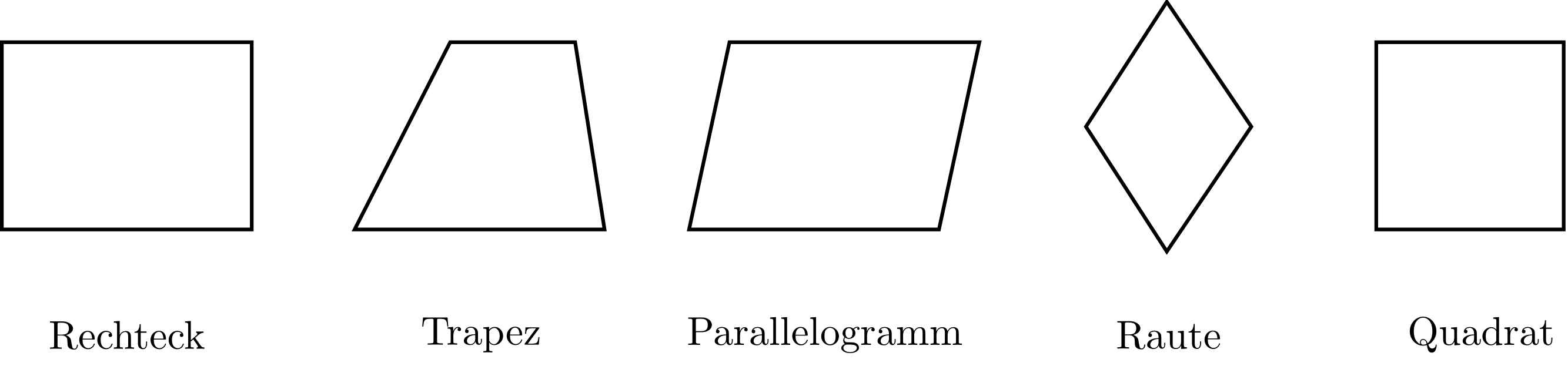
Für Vierecke mit den folgenden weiteren Eigenschaften werden eigene Begriffe eingeführt: Ein Viereck heißt
Für Vierecke mit den folgenden weiteren Eigenschaften werden eigene Begriffe eingeführt: Ein Viereck heißt
- Trapez, falls wenigstens zwei Seiten parallel sind;
- Parallelogramm, falls je zwei
gegenüberliegende Seiten parallel sind;
- Raute oder
gleichseitiges Viereck oder
auch Rhombus, falls alle vier Seiten gleich lang sind;
- Rechteck, falls alle vier (Innen-)Winkel rechte
Winkel sind;
- Quadrat, falls es ein Rechteck ist, bei dem alle
Seiten gleich lang sind;
- Einheitsquadrat, falls es ein Quadrat mit
Seitenlänge ist.
Unter den gerade eingeführten speziellen Vierecken gibt es eine ganze Reihe von Zusammenhängen:
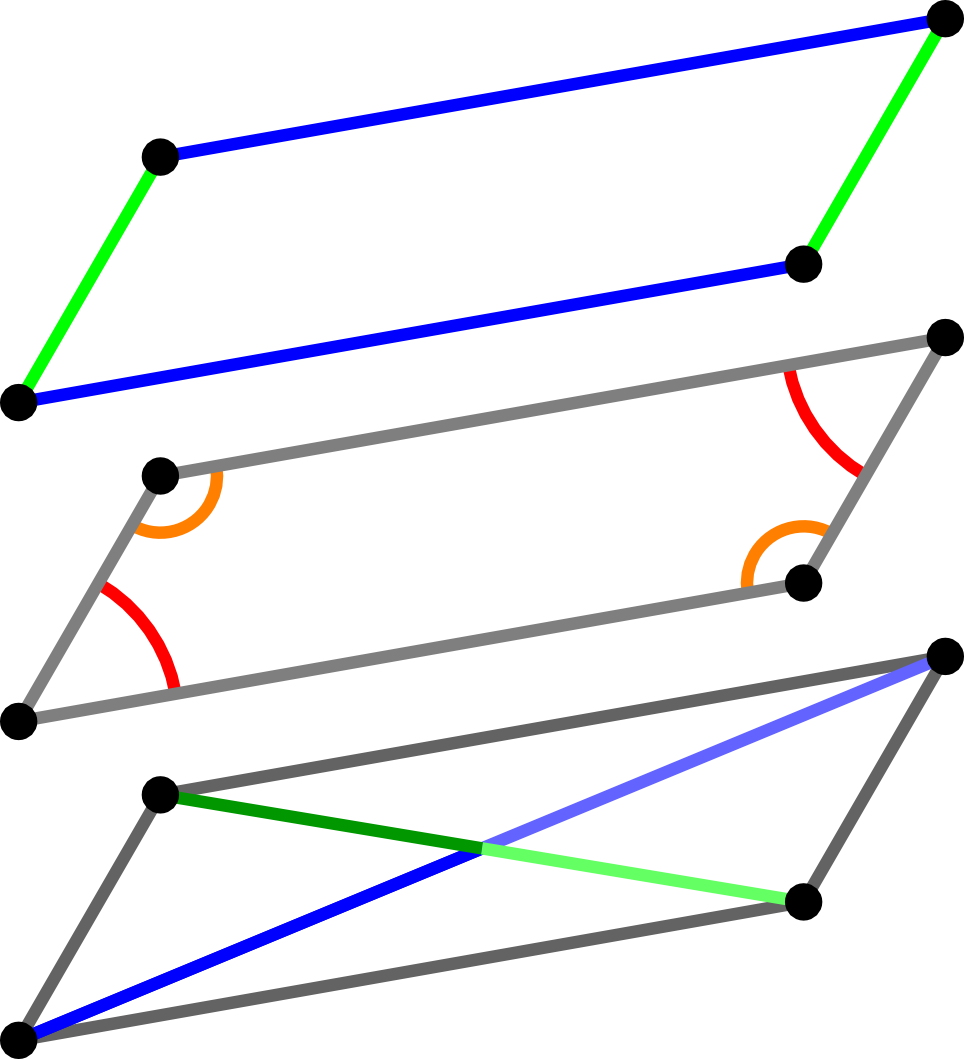
Diese Vierecke können auf vielerlei Weisen anhand von Eigenschaften der Seiten, Winkel oder auch Diagonalen charakterisiert werden.
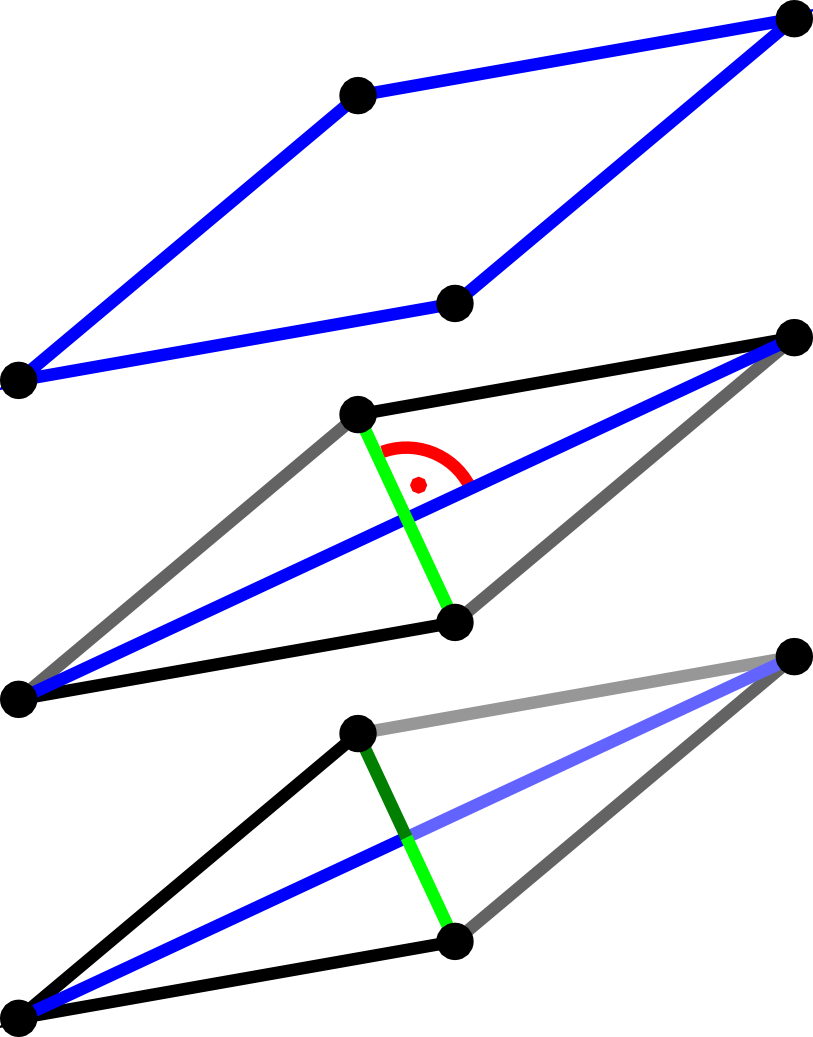
Rauten können als besondere Parallelogramme beschrieben werden.
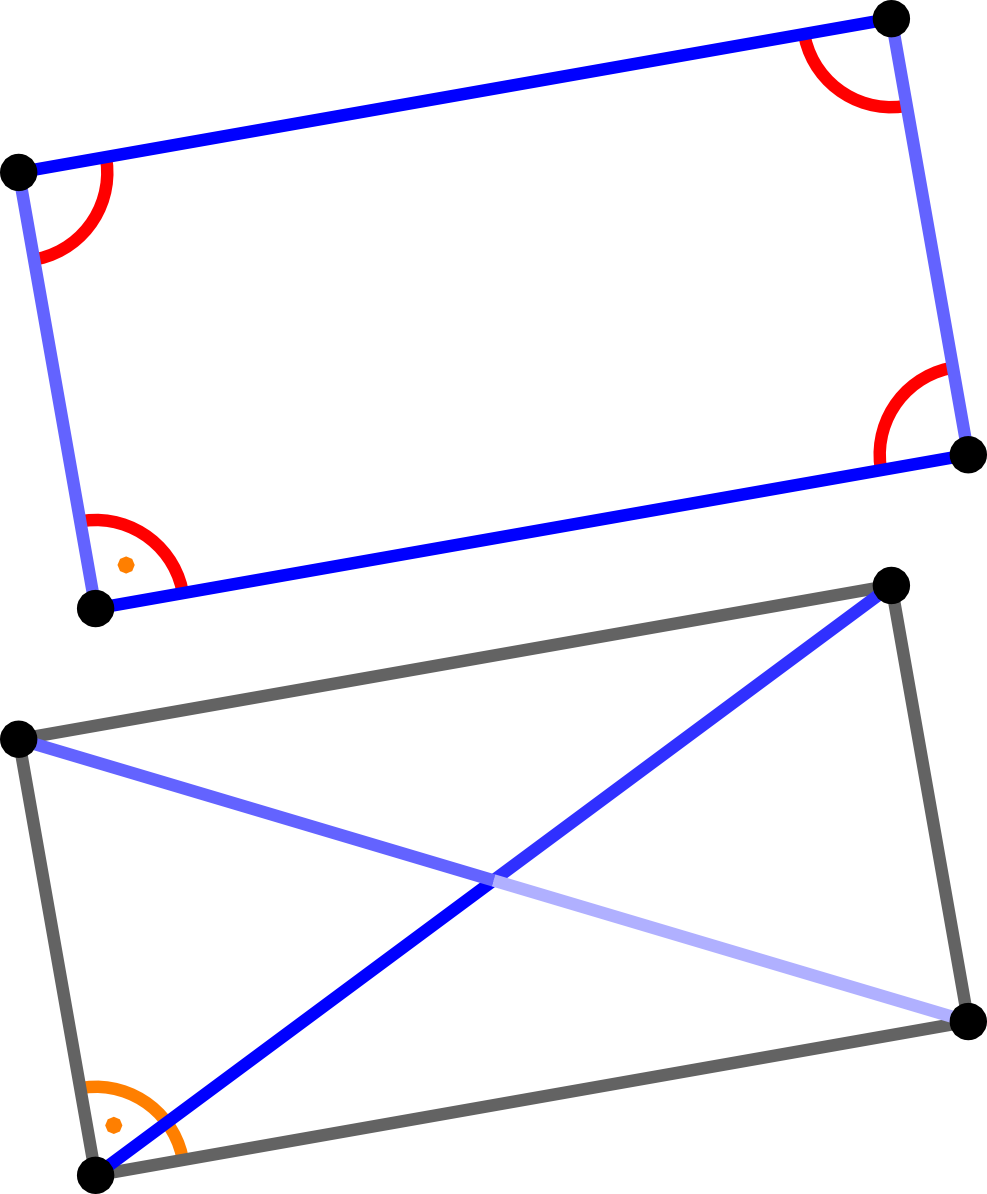
Bei Rechtecken denkt man oft an rechte Winkel, wie es ihr Name andeutet. Darüber hinaus können Rechtecke mit Hilfe von Eigenschaften ihrer Diagonalen einfach beschrieben werden.
Rechteck
5.4.6
|
Quadrate sind sowohl besondere Recktecke als auch spezielle Rauten.
Quadrat
5.4.7
|