Onlinebrückenkurs Mathematik Abschnitt 5.3.2 Dreiecke

Kapitel 5 Geometrie - Abschnitt 5.3 Rund um Dreiecke

5.3.2 Dreiecke

Viele Aussagen über geometrische Figuren und Körper ergeben sich aus Eigenschaften von Dreiecken, der „einfachsten geschlossenen Figur“, die durch drei Punkte bestimmt wird, die nicht auf einer Geraden liegen.

Zunächst werden die wichtigsten Begriffe zusammengestellt, bevor Fragen beantwortet werden, wann Dreiecke eindeutig bestimmt sind und wie einzelne Seitenlängen oder Winkel berechnet werden können. Hierbei sind die Strahlensätze ein wichtiges Hilfsmittel, die auch als Aussagen über Beziehungen zwischen Dreiecken gesehen werden können.

Funktionale Beziehungen zwischen Seitenlängen und Winkel werden dann im Abschnitt 5.6 betrachtet, um weitergehende Fragestellungen beantworten zu können, die für Anwendungen relevant sind.

Dreieck 5.3.1
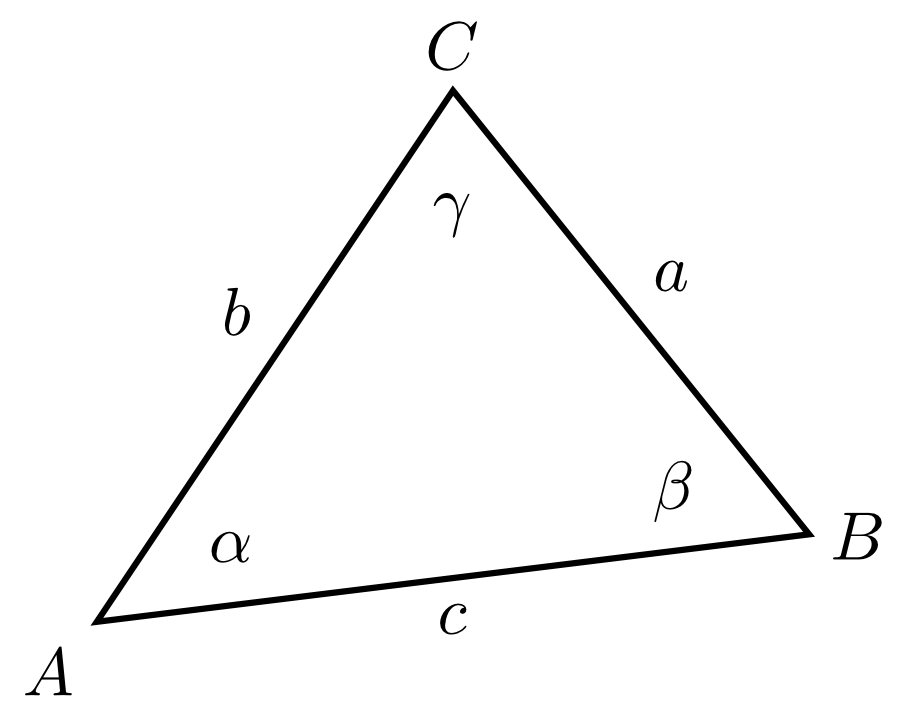
Ein Dreieck entsteht, wenn man drei Punkte

A

B

und

C

, die nicht auf einer Geraden liegen, verbindet. Dieses Dreieck wird dann mit

A B C

bezeichnet.

Die drei Punkte, die verbunden werden, heißen Ecken des Dreiecks, und die drei Verbindungslinien heißen Seiten des Dreiecks.
Je zwei Seiten des Dreiecks bilden je zwei Winkel.

Der kleinere dieser beiden Winkel heißt Innenwinkel (oft kurz Winkel genannt), und der größere der beiden Winkel heißt Außenwinkel.
Die Summe der drei Innenwinkel eines Dreiecks ist $180^{\circ}$ beziehungsweise $π$ .

Eine oft verwendete Art, die Größen eines Dreiecks zu bezeichnen, ist folgende: Man benennt die Ecken eines Dreiecks in „mathematisch positiver“ Richtung (gegen den Uhrzeigersinn) mit lateinischen Großbuchstaben. Die einer Ecke gegenüberliegende Seite eines Dreiecks bekommt den entsprechenden Kleinbuchstaben zugeordnet, und der Innenwinkel in einer Ecke erhält den entsprechenden Kleinbuchstaben des griechischen Alphabets.

Da die Außenwinkel eines Dreiecks wesentlich weniger interessant sind als die Innenwinkel, nennt man die Innenwinkel eines Dreiecks auch schlicht Winkel des Dreiecks.

Die Summe aller (Innen-)Winkel in einem Dreieck beträgt

180^{\circ}

beziehungsweise

π

. Somit kann höchstens ein Winkel gleich oder größer als

90^{\circ}

beziehungsweise

\frac{π}{2}

sein. Dementsprechend werden die Dreiecke nach ihrem größten Winkel in drei verschiedene Klassen eingeteilt:

Bezeichungen für Dreiecke 5.3.2
Dreiecke werden folgendermaßen nach ihren Winkeln benannt:

Ein Dreieck, in dem alle Winkel kleiner als $\frac{π}{2}$ sind, heißt spitzwinklig.
Ein Dreieck, das einen rechten Winkel enthält, heißt rechtwinklig.

In einem rechtwinkligen Dreieck heißen die Seiten, die auf den Schenkeln des rechten Winkels liegen, Katheten, und die Seite, die dem rechten Winkel gegenüberliegt, heißt Hypotenuse.
Ein Dreieck, das einen Winkel mit einem Maß von über $\frac{π}{2}$ besitzt, heißt stumpfwinklig.

Es wird eine einfache Konstruktion eines Wagenhebers in der Form eines Dreiecks betrachtet: Er besteht aus zwei Stäben, die durch ein Gelenk miteinander verbunden sind. Die anderen Endpunkte der beiden Stäbe können zusammengezogen werden können. Je großer der Winkel eines Stabs gegenüber der Straße ist, desto höher befindet sich das Gelenk über dem Boden.

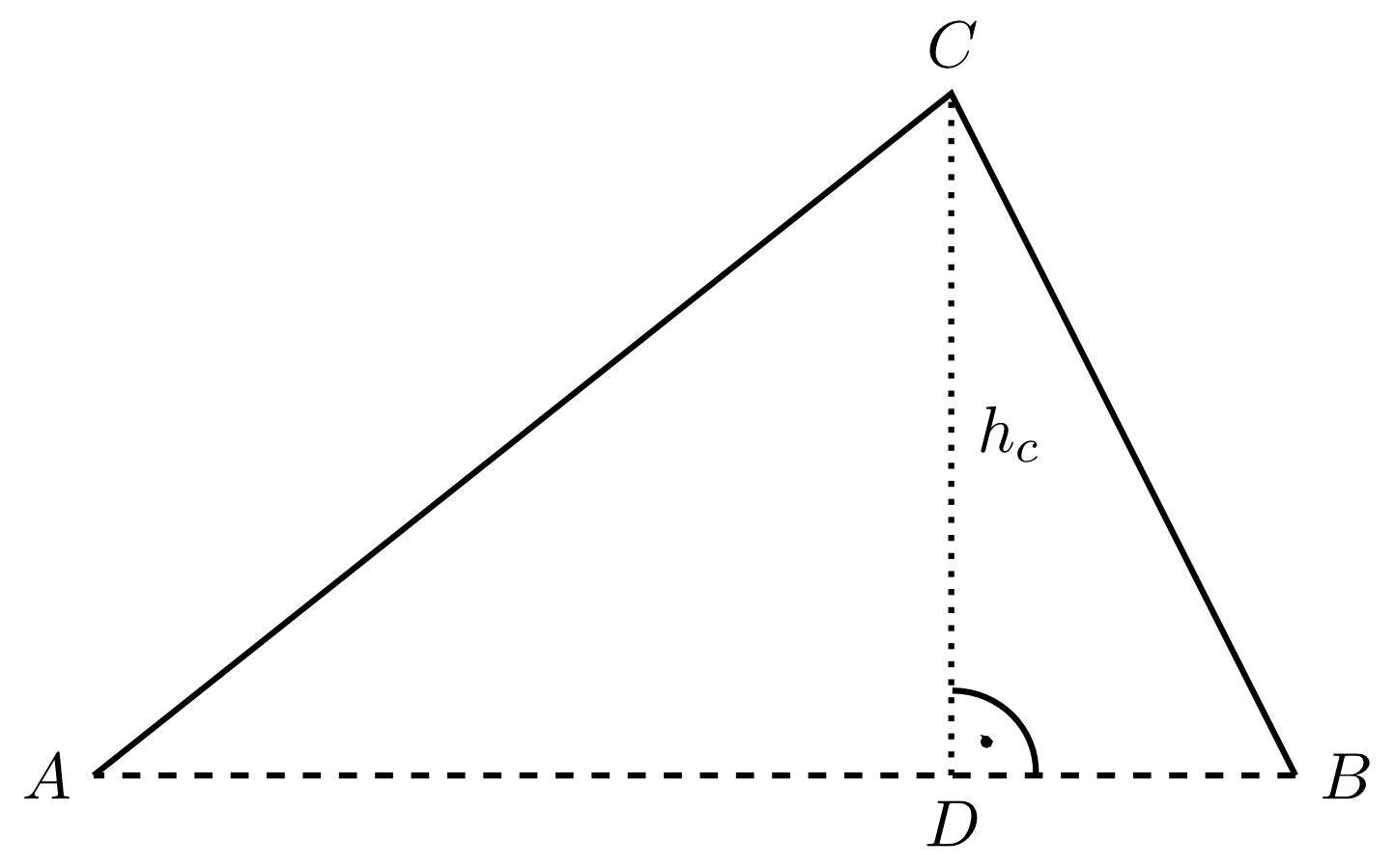
So wird in einem Dreieck

A B C

die kürzeste Strecke zwischen der Ecke

C

und der Geraden, die durch die gegenüberliegende Seite

c

bestimmt ist, die Höhe eines Dreiecks

h_{c}

auf die Seite

c

genannt. Der andere Endpunkt

D

der Strecke

h_{c}

heißt Höhenfußpunkt. Entsprechend werden die Höhen

h_{a}

und

h_{b}

definiert.

Man kann auch sagen, dass die Höhen diejenigen Strecken sind, die senkrecht auf der Geraden einer Seite stehen und bis zu einer Ecke des Dreiecks gehen.