1.1.1 Einführung
Die Mathematik ist eine Wissenschaft, in der allgemein abstrakte Strukturen und deren logische Zusammenhänge untersucht werden. Bevor auf die eigentlichen Inhalte dieses Abschnitts näher eingegangen wird, soll kurz auf den grundlegenden Begriff der Menge Bezug genommen werden.
Info
1.1.1
Um Aussagen in kompakter Weise über eine Reihe von strukturell ähnlichen Objekten treffen zu können, kann man solche Objekte in Mengen zusammenfassen, die als Behältnis für die Objekte dienen. Seien die Objekte mit benannt, dann bildet das Symbol die Menge , welche die vorigen Objekte als Elemente enthält. Letzteres schreibt man kurz , , usw.; das Zeichen „“ bedeutet also „ist Element von“. (Manchmal ist es schreibtechnisch geboten, die Reihenfolge von Element und Menge auszutauschen. Zum Erhalten der gleichen Aussage(n) wird dann das -Symbol umgedreht, d.h. , , usw. heißt dann dasselbe, wobei „“ somit „enthält als Element“ bzw. „beinhaltet“ bedeutet.)
Neben der aufzählenden Schreibweise von Mengen existieren weitere Schreibweisen. Wenn die Elemente z.B. eine Bedingung erfüllen sollen, dann schreibt man . Wird dabei (explizit) aus einer umfassenderen Menge entnommen, dann wird dies auch in der Form oder kurz geschrieben.
Aussagen wie „“ oder „“ sind Aussagen im mathematischen Sinn, d.h. ihnen kann ein eindeutiger Wahrheitswert „wahr“ oder „falsch“ zugeordnet werden. Seien und solche Aussagen. Für den Fall, dass sowohl als auch gelten soll, also und gelten sollen, schreibt man auch . Im Fall, dass nur eine von beiden Aussagen zu gelten braucht, d.h. oder (oder beide Aussagen) gelten sollen, schreibt man auch .
Für zwei Mengen und notiert man
Um Aussagen in kompakter Weise über eine Reihe von strukturell ähnlichen Objekten treffen zu können, kann man solche Objekte in Mengen zusammenfassen, die als Behältnis für die Objekte dienen. Seien die Objekte mit benannt, dann bildet das Symbol die Menge , welche die vorigen Objekte als Elemente enthält. Letzteres schreibt man kurz , , usw.; das Zeichen „“ bedeutet also „ist Element von“. (Manchmal ist es schreibtechnisch geboten, die Reihenfolge von Element und Menge auszutauschen. Zum Erhalten der gleichen Aussage(n) wird dann das -Symbol umgedreht, d.h. , , usw. heißt dann dasselbe, wobei „“ somit „enthält als Element“ bzw. „beinhaltet“ bedeutet.)
Neben der aufzählenden Schreibweise von Mengen existieren weitere Schreibweisen. Wenn die Elemente z.B. eine Bedingung erfüllen sollen, dann schreibt man . Wird dabei (explizit) aus einer umfassenderen Menge entnommen, dann wird dies auch in der Form oder kurz geschrieben.
Aussagen wie „“ oder „“ sind Aussagen im mathematischen Sinn, d.h. ihnen kann ein eindeutiger Wahrheitswert „wahr“ oder „falsch“ zugeordnet werden. Seien und solche Aussagen. Für den Fall, dass sowohl als auch gelten soll, also und gelten sollen, schreibt man auch . Im Fall, dass nur eine von beiden Aussagen zu gelten braucht, d.h. oder (oder beide Aussagen) gelten sollen, schreibt man auch .
Für zwei Mengen und notiert man
- , d.h. ist (unechte) Teilmenge von , wenn jedes
Element von auch in enthalten ist; gibt es dann mindestens ein Element
in , das nicht in enthalten ist, wenn also eine echte Teilmenge von
ist, so schreibt man (auch) ;
- für die Vereinigung der beiden Mengen; diese bezeichnet
jene Menge, die alle Elemente enthält, die in mindestens einer der beiden
Mengen vorkommen;
- für den Schnitt der beiden Mengen; dieser bezeichnet
jene Menge, in der alle Elemente enthalten sind, die in beiden Mengen
vorkommen;
- für die Differenzmenge, d.h. für diejenige Menge,
welche die Elemente von enthält, die nicht in vorkommen.
Mathematik beinhaltet die Welt der Zahlen:
Wenn man verschiedene Zahlen näher betrachtet, so erkennt man jedoch grundlegende Unterschiede. Manche Zahlen lassen sich nicht als geschlossener Dezimalbruch darstellen, andere sind schier unvorstellbar (imaginär), wieder andere kann man an den Fingern abzählen oder aber als Lösungen von Gleichungen gewinnen.
Info
1.1.2
Die in diesem Kurs verwendeten Zahlenbereiche sind:
Die in diesem Kurs verwendeten Zahlenbereiche sind:
| die Menge der natürlichen Zahlen ohne Null, | |
| die Menge der natürlichen Zahlen inklusive Null, | |
| die Menge der ganzen Zahlen, | |
| die Menge der rationalen Zahlen (Brüche), | |
| die Menge der reellen Zahlen. |
Diese Zahlenbereiche sind nicht unabhängig voneinander, sondern bilden eine Kette ineinandergeschachtelter Zahlenmengen:
Diese Zahlenbereiche erhält man, indem man sich nacheinander die Lösungen folgender Gleichungen anschaut und die Zahlenbereiche so erweitert, dass immer eine Lösung existiert:
| Zahlenbereich | lösbare Gleichung | nicht lösbar | Hinzunahme | neuer Bereich |
| negativer Zahlen | ||||
| von Brüchen | ||||
| irrationaler Zahlen | ||||
| usw. |
Natürliche Zahlen treten immer dann auf, wenn Anzahlen bestimmt oder Dinge nummeriert werden müssen. Sie spielen in der Kombinatorik eine große Rolle: die Anzahl der Möglichkeiten, aus 49 Kugeln 6 Kugeln zu ziehen, ist zum Beispiel eine natürliche Zahl. In der Informatik bilden sie die Grundlage für die verschiedenen Zahlensysteme: das Dualsystem hat die Basis 2, das Dezimalsystem die Basis 10 und das Hexadezimalsystem die Basis 16. Bestimmte natürliche Zahlen, die Primzahlen, bilden die Grundlage der modernen Verschlüsselungstechniken.
In der Menge der natürlichen Zahlen lässt es sich einfach rechnen, aber man stoßt an Grenzen, wenn man zum Beispiel eine Temperaturangabe von 3C liest (handelt es sich um Plus- oder Minusgrade?) oder eine Gleichung der Form auflösen möchte. Daher muss die Menge der natürlichen Zahlen um die negativen natürlichen Zahlen erweitert werden und man erhält . Die Menge der ganzen Zahlen wird mit
bezeichnet. Ganze Zahlen werden immer dann benötigt, wenn das Vorzeichen der natürlichen Zahlen eine Rolle spielt. In können Zahlen voneinander subtrahiert werden, d.h. Gleichungssysteme der Form sind in immer lösbar ().
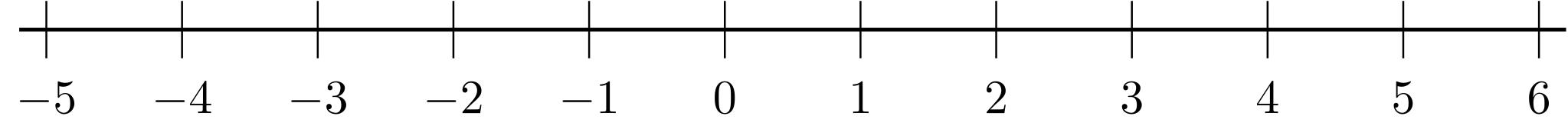
Abbildung 1.1.1: Skizze (C)
Auf den ganzen Zahlen lässt sich eindeutig ein Vergleichssymbol definieren, die ganzen Zahlen lassen sich damit zu einer Kette anordnen:
Eine rationale Zahl stellt das Verhältnis zweier ganzer Zahlen dar:
Dabei ist zu beachten, dass die Darstellung als Bruch nicht eindeutig ist, man kann die gleiche Zahl durch mehrere Brüche beschreiben. Beispielsweise ist
die gleiche rationale Zahl.
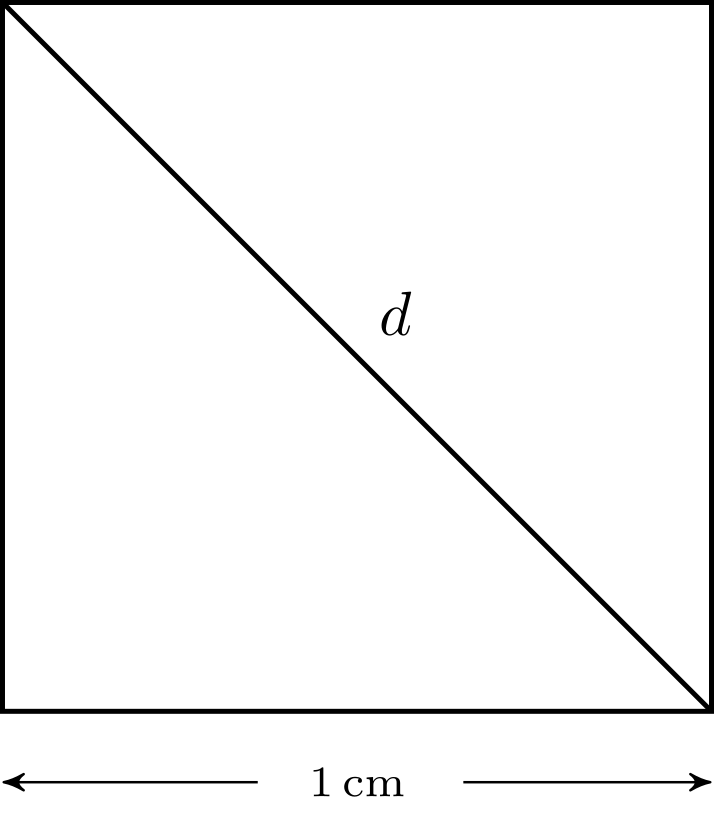
Andererseits kann nicht jede Zahl auf dem Zahlenstrahl als Bruch dargestellt werden. Betrachtet man zum Beispiel ein Quadrat mit der Seitenlänge 1 und will die Länge der Diagonalen berechnen, so erhält man nach dem Satz von Pythagoras:
|
|
Eine weitere Zahl, die nicht als Bruch dargestellt werden kann, erhält man durch Abrollen eines Rades mit Durchmesser auf der Zahlengeraden. Es handelt sich um die Zahl . Man kann zeigen, dass diese beiden Zahlen ( und ) nicht in Form eines Bruchs geschrieben werden können. (Der Beweis für ist dabei verhältnismäßig einfach.) Sie sind zwei Beispiele aus der Menge der sogenannten irrationalen Zahlen.
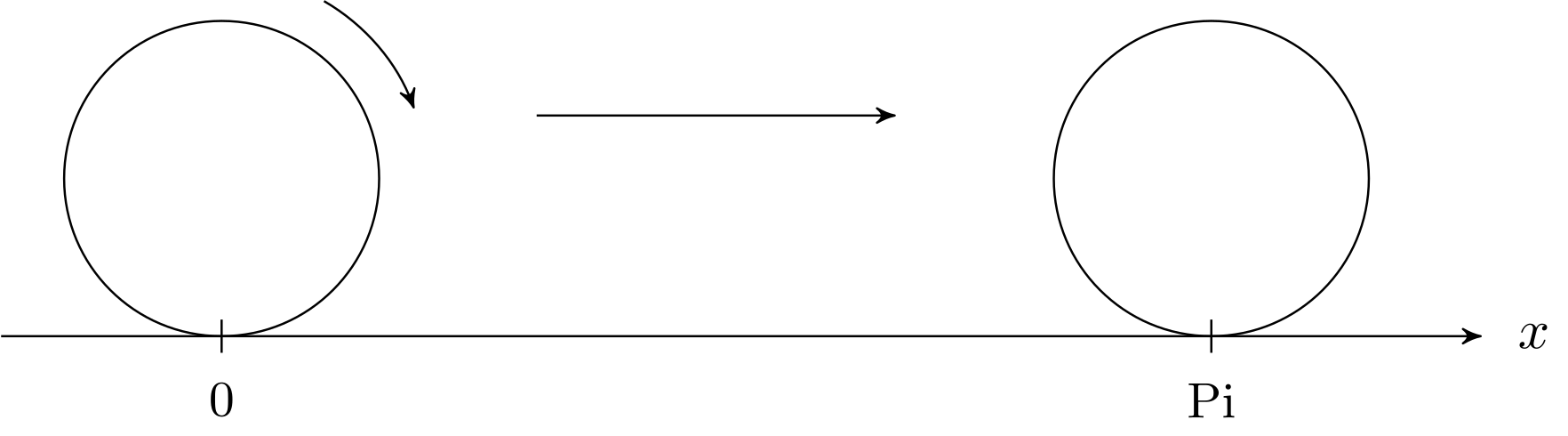
Abbildung 1.1.3: Skizze (C)
Eine Zahl ist irrational, wenn sie nicht rational ist, also nicht als Bruch aufgeschrieben werden kann. Die irrationalen Zahlen schließen nun die noch vorhandenen Lücken auf der Zahlengeraden, jedem Punkt entspricht genau eine reelle Zahl.
Reelle Zahlen dienen als Maßzahlen für Längen, Flächeninhalte, Temperaturen, Massen, etc. In diesem Kurs werden die mathematischen Probleme typischerweise mit reellen Zahlen gelöst.
Eine Grundeigenschaft reeller Zahlen ist, dass diese geordnet sind, d.h. für zwei reelle Zahlen gilt genau eine der drei Beziehungen , oder . Eine weitere definierende Eigenschaft ist die Vollständigkeit, die - grob gesprochen - die „Lückenlosigkeit“ der Zahlengeraden beschreibt.
Info
1.1.5
Für zwei verschiedene reelle Zahlen betrachtet man insbesondere alle Zahlen, die auf der Zahlengeraden zwischen diesen beiden Zahlen liegen. Solche Teilmengen reeller Zahlen bezeichnet man als Intervalle. Deren Beschreibung wird so festgelegt, dass man ihnen eine linke Intervallgrenze () und eine rechte Intervallgrenze zuordnet mit . Je nachdem, ob eine oder beide Intervallgrenzen zum Intervall dazugehören, ergeben sich folgende Fälle:
Im Falle offener Intervallenden kann man auch unbeschränkte Intervalle betrachten. In diesen Fällen entfällt die jeweilige Bedingung in der Mengenbeschreibung: , , , , .
Darüber hinaus sind folgende Bezeichnungen gebräuchlich: , , , .
Für zwei verschiedene reelle Zahlen betrachtet man insbesondere alle Zahlen, die auf der Zahlengeraden zwischen diesen beiden Zahlen liegen. Solche Teilmengen reeller Zahlen bezeichnet man als Intervalle. Deren Beschreibung wird so festgelegt, dass man ihnen eine linke Intervallgrenze () und eine rechte Intervallgrenze zuordnet mit . Je nachdem, ob eine oder beide Intervallgrenzen zum Intervall dazugehören, ergeben sich folgende Fälle:
- bezeichnet das abgeschlossene Intervall
zwischen und , bei dem die Grenzen zum Intervall dazugehören.
- bezeichnet das offene Intervall
zwischen und , bei dem die Grenzen nicht zum Intervall
dazugehören.
- bezeichnet das links abgeschlossene und
rechts offene Intervall zwischen und , bei dem die linke Grenze
zum Intervall dazugehört, die rechte aber nicht.
- bezeichnet das links offene und
rechts abgeschlossene Intervall zwischen und , bei dem die rechte
Grenze zum Intervall dazugehört, die linke aber nicht.
Im Falle offener Intervallenden kann man auch unbeschränkte Intervalle betrachten. In diesen Fällen entfällt die jeweilige Bedingung in der Mengenbeschreibung: , , , , .
Darüber hinaus sind folgende Bezeichnungen gebräuchlich: , , , .