2. Integralrechnung
  3. Bestimmtes Integral
  4. Eigenschaften des Integrals

8.2.4 Eigenschaften des Integrals



Für ungerade Funktionen f:[-c;c]→ℝ ist das Integral Null. Dies soll am Beispiel der Funktion f auf [-2;2] mit f(x)= x3 erläutert werden:
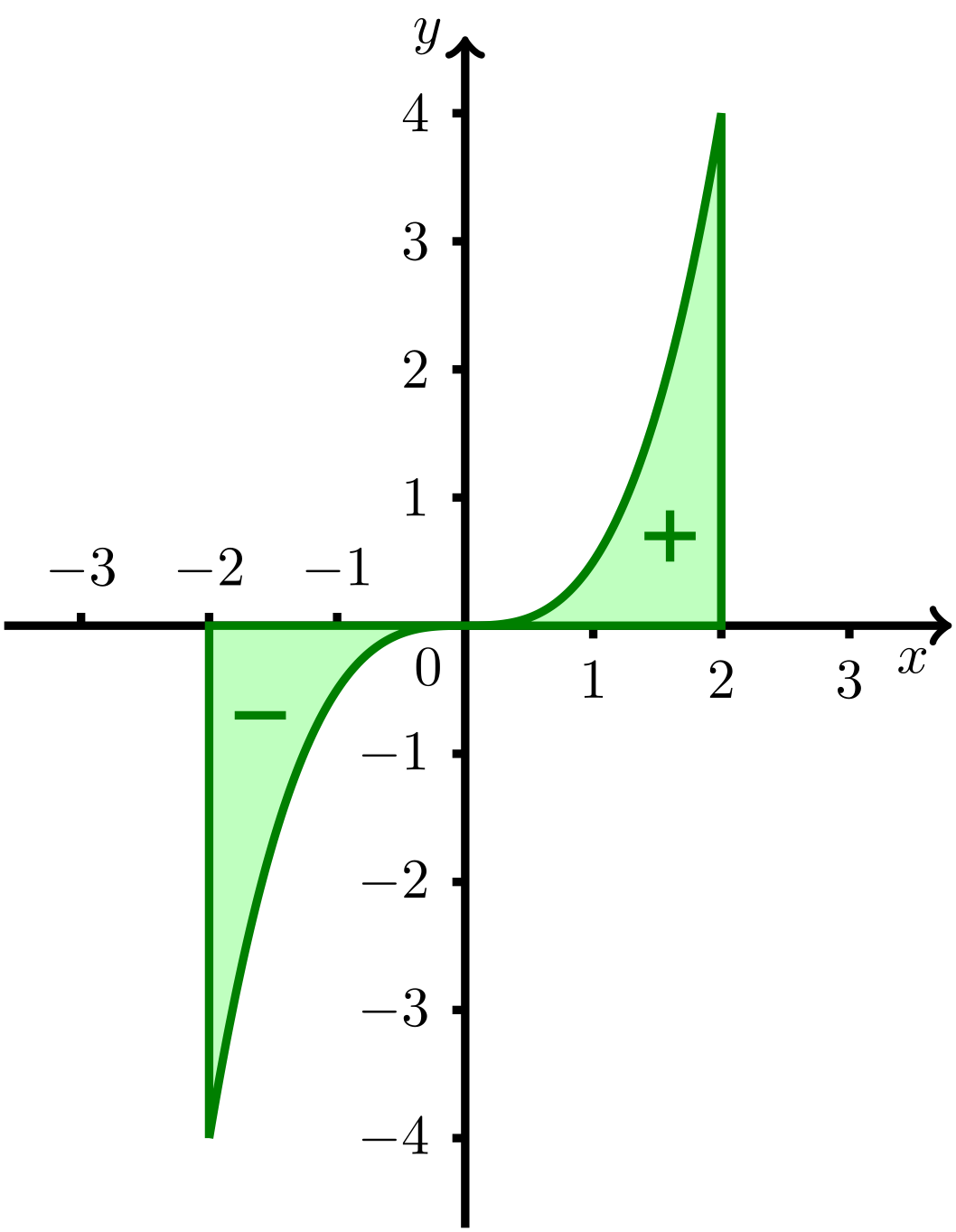
./_95BF70DE_4x.png
Abbildung 8.2.2: Skizze  (C)



Man teilt den Graphen von f in zwei Teile zwischen -2 und 0 bzw. 0 und 2 ein und untersucht die Teilflächen, die der Graph in beiden Bereichen mit der x-Achse einschließt. Man kann die beiden Teilflächen durch eine Punktspiegelung ineinander überführen. Beide Teilflächen sind gleich groß. Bildet man jeweils die Riemann-Summen, dann stellt man fest, dass Flächen, die unterhalb der x-Achse liegen, im Integral einen negativen Wert annehmen. Wenn man also die beiden hier abgebildeten Teilflächen addiert, um das Integral über den gesamten Bereich von -2 bis 2 zu berechnen, erhält die Fläche über der positiven x-Achse einen positiven Wert, während die Fläche unterhalb der negativen x-Achse gleich groß ist, aber einen negativen Wert annimmt. Die Summe der beiden Teilflächen ist also Null. Für ungerade Funktionen f gilt die Regel:



∫-c c f(x) dx=0 .



Im Fall einer geraden Funktion g:[-c;c]→ℝ ist der Graph symmetrisch bezüglich der y-Achse.
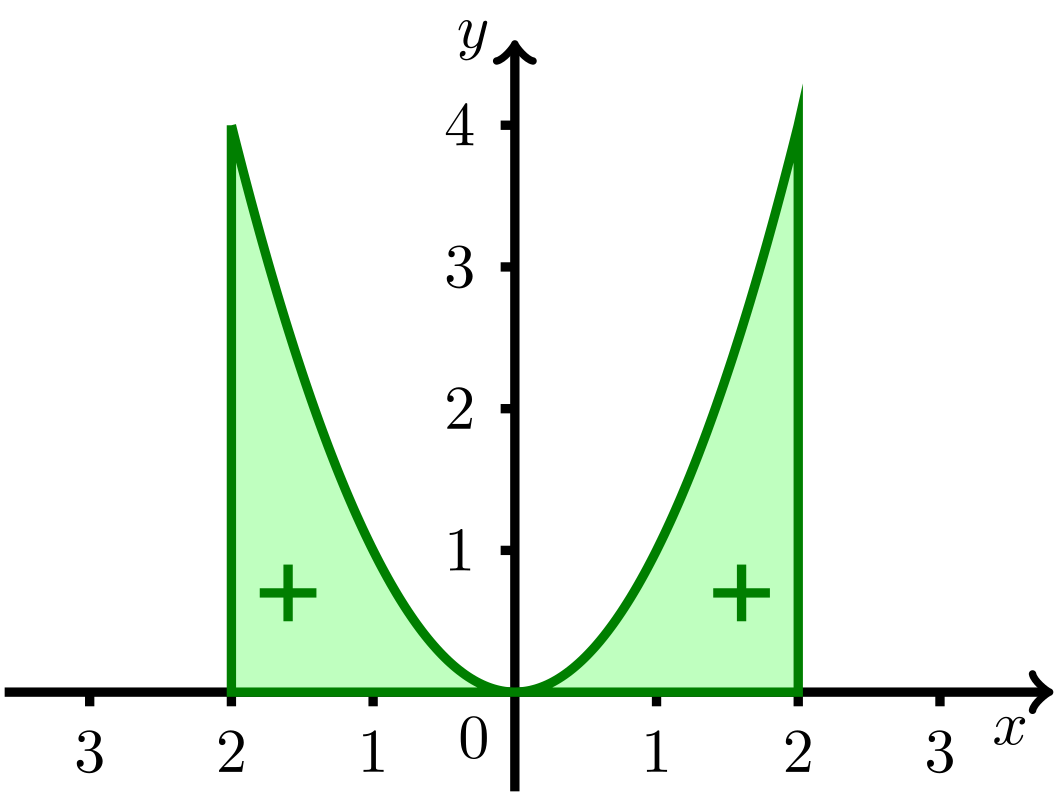
./_2691D46C_4x.png
Abbildung 8.2.3: Skizze  (C)

Die Fläche zwischen dem Graphen von g und der x-Achse ist hier symmetrisch bezüglich der y-Achse. Die Teilfläche links davon ist also das Spiegelbild der rechts liegenden Fläche. Beide zusammen ergeben die Gesamtfläche



∫-c c g(x) dx=2· ∫0 c g(x) dx .



Diese Regel für das Integral gilt für jede integrierbare Funktion g, die gerade ist, auch wenn es negative Funktionswerte gibt. Aufgrund der Rechenregel genügt es dann, das Integral für nichtnegative x-Werte mit der Untergrenze 0 und der Obergrenze c zu berechnen.

In sehr vielen Situationen wird die Berechnung eines Integrals einfacher, wenn man den Integranden vor der Integration in eine bekannte Form bringt. Beispiele zu möglichen Umformungen sollen im Folgenden betrachtet werden. Im ersten Beispiel werden Potenzfunktionen untersucht.

Beispiel 8.2.13  
Es soll das Integral

∫1 4 (x-2)·x dx

berechnet werden. Um die Rechnung zu vereinfachen, formt man den Integranden um:

(x-2)·x=xx-2x= x 3 2 -2 x 1 2  .

Damit kann man das Integral einfacher lösen:

∫1 4 (x-2)·x dx = ∫1 4 ( x 3 2 -2 x 1 2 )dx= [ 2 5 x 5 2 - 4 3 x 3 2 ]1 4 = ( 2 5 (4)5 - 4 3 (4)3 )-( 2 5 ·1- 4 3 ·1) = ( 64 5 - 32 3 )-( 2 5 - 4 3 ) = 62 5 - 28 3 = 3+ 1 15  .



Im nächsten Beispiel wird die Umformung eines Integranden mit Exponentialfunktionen durchgeführt.

Beispiel 8.2.14  
Es wird das Integral

∫-2 3 8e3+x -12e2x 2ex  dx

berechnet. Mit den Rechenregeln für die Exponentialfunktion erhält man

8e3+x -12e2x 2ex = 8e3+x 2ex - 12e2x 2ex =4e3+x-x -6e2x-x =4e3 -6ex  ,

sodass das Integral schließlich auf sehr einfache Art und Weise gelöst werden kann:

∫-2 3 8e3+x -12e2x 2ex  dx= ∫-2 3 (4e3 -6ex )dx = [4e3 ·x-6ex ]-2 3 = (4e3 ·3-6e3 )-(4e3 ·(-2)-6e-2 ) = 14e3 + 6 e2  .



Ist bei einer rationalen Funktion der Grad des Zählerpolynoms größer oder gleich dem Grad des Nennerpolynoms, dann führt man zunächst eine Polynomdivision (siehe Modul 6) durch. Je nach Situation können sich auch noch weitere Umformungen (z.B. Partialbruchzerlegung) anbieten, die man in der weiterführenden Literatur und Formelsammlungen finden kann. Im folgenden Beispiel wird eine Polynomdivision durchgeführt, um eine rationale Funktion zu integrieren.

Beispiel 8.2.15  
Es wird das Integral

∫-1 1 4 x2 -x+4 x2 +1  dx

berechnet. Dazu formt man zunächst den Integranden mittels Polynomdivision

4 x2 -x+4=( x2 +1)·4-x

zu

4 x2 -x+4 x2 +1 =4- x x2 +1

um. Damit ist dann

∫-1 1 4 x2 -x+4 x2 +1  dx = ∫-1 1 (4- x x2 +1 )dx = ∫-1 1 4 dx- ∫-1 1 x x2 +1  dx= [4x]-1 1 -0=8 .

Denn der Integrand des zweiten Integrals ist eine ungerade Funktion und im Integrationsintervall [-1;1] punktsymmetrisch, sodass der Wert des zweiten Integrals Null ist.

Hier wurde eine besondere Situation gewählt, um einen ersten Eindruck zur Integration rationaler Funktionen zu vermitteln. In weiterführenden mathematischen Vorlesungen oder in der Literatur wird dies allgemein beschrieben.