9.3.3 Koordinatengleichungen für Kreise
Hat man in der Ebene ein Koordinatensystem zur Verfügung, so kann man nun die Punkte auf einem Kreis unter Verwendung des Abstandsbegriffs aus dem vorigen Abschnitt 9.3.2 mit Hilfe einer Gleichung, der sogenannten Kreisgleichung, beschreiben. In der Praxis möchte man sich die, in der Abstandsformel obligatorische, Wurzel ersparen und benutzt stattdessen das Quadrat des Abstands. Dies ist möglich, da Abstände immer nicht-negativ sind. Es gilt also für zwei Punkte und :
Dies wird in der folgenden Infobox zusammengefasst:
Info
9.3.4
Ein Kreis in der Ebene mit einem vorgegebenen Koordinatensystem ist die Menge aller Punkte, die einen festen Abstand , den sogenannten Radius, zu einem gemeinsamen Mittelpunkt besitzen. Die Angabe des Radius und des Mittelpunkts legt den Kreis eindeutig fest. Also gilt:
So wie bei Geraden gibt man auch für Kreise oft nur die Kreisgleichung an:
Es gehören also alle diejenigen Punkte zum Kreis, deren Koordinaten die Kreisgleichung erfüllen. Bild hierzu:
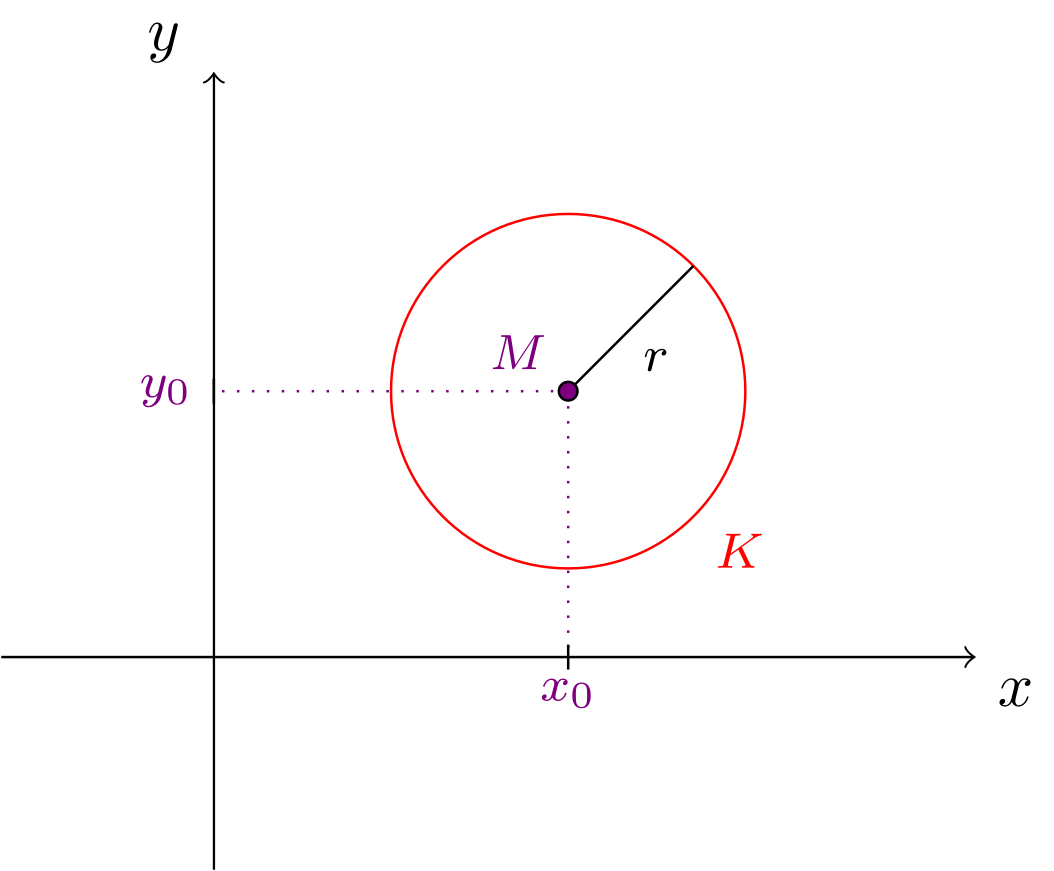
Ein Kreis in der Ebene mit einem vorgegebenen Koordinatensystem ist die Menge aller Punkte, die einen festen Abstand , den sogenannten Radius, zu einem gemeinsamen Mittelpunkt besitzen. Die Angabe des Radius und des Mittelpunkts legt den Kreis eindeutig fest. Also gilt:
So wie bei Geraden gibt man auch für Kreise oft nur die Kreisgleichung an:
Es gehören also alle diejenigen Punkte zum Kreis, deren Koordinaten die Kreisgleichung erfüllen. Bild hierzu:

Abbildung 9.3.5: Skizze (C)
Mit Hilfe der Kreisgleichung können nun beliebige Kreise in der Ebene sowie Punkte auf diesen Kreisen und solche, die nicht auf diesen Kreisen liegen, beschrieben werden.
Beispiel
9.3.5
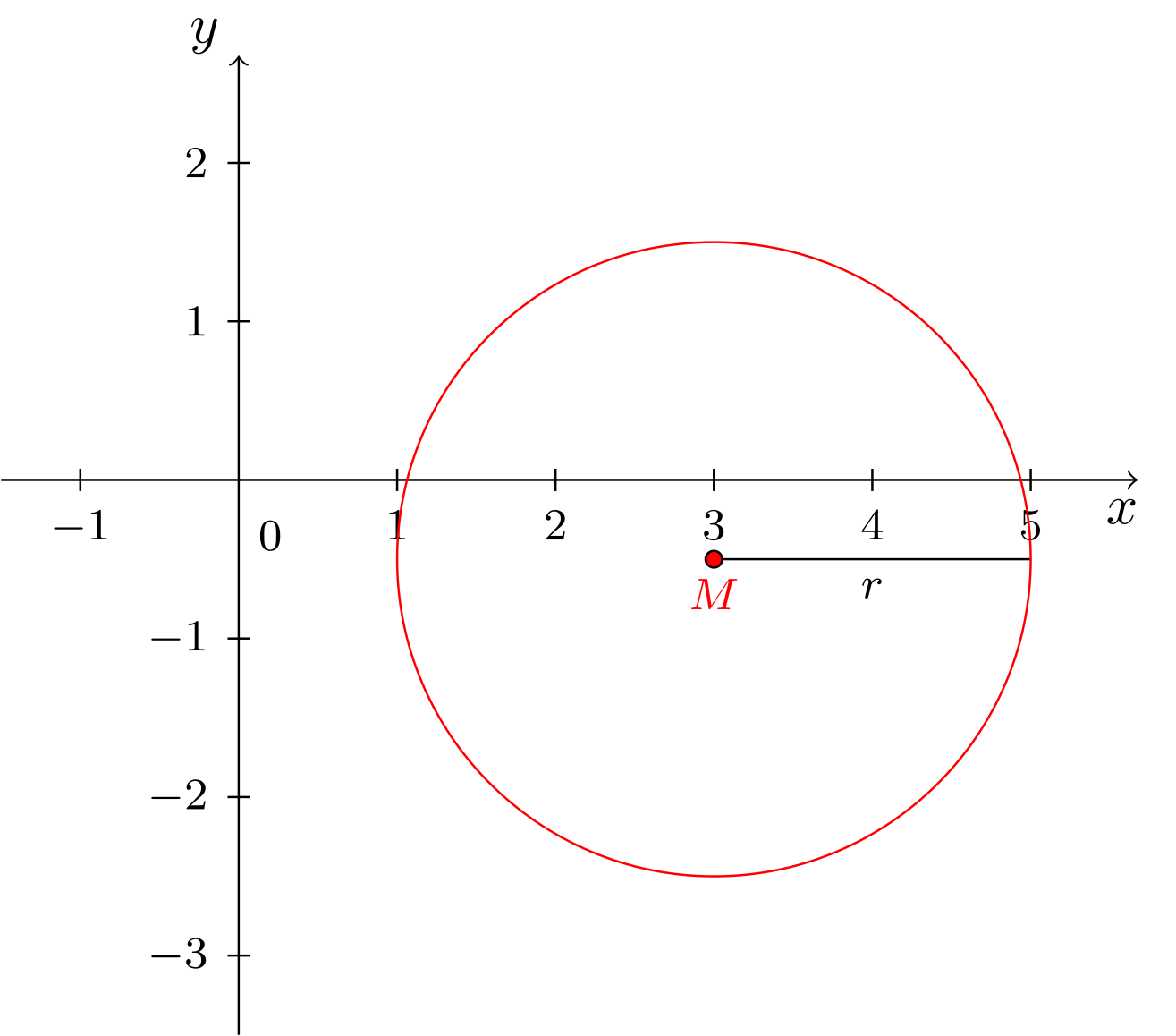
Der Kreis mit Mittelpunkt und Radius wird beschrieben durch die Kreisgleichung
Auf dem Kreis liegen also alle Punkte, die von den Abstand haben. Beispielsweise ist ein Punkt auf dem Kreis, da
gilt. dagegen ist kein Punkt auf dem Kreis, denn er besitzt den Abstand
Der Punkt erfüllt also nicht die Kreisgleichung.

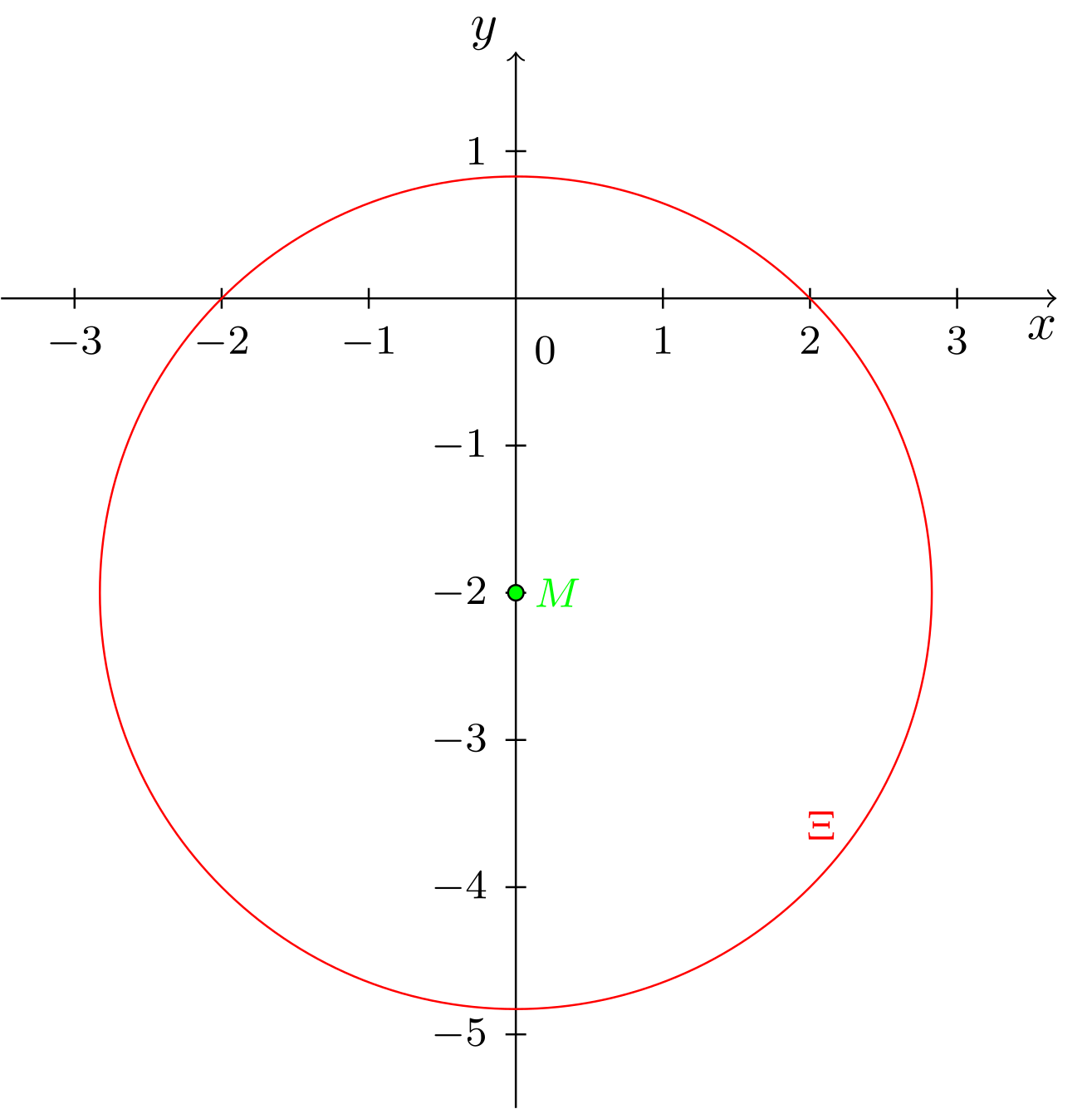
Der Kreis mit Mittelpunkt und Radius wird beschrieben durch die Kreisgleichung
Auf dem Kreis liegen also alle Punkte, die von den Abstand haben. Beispielsweise ist ein Punkt auf dem Kreis, da
gilt. dagegen ist kein Punkt auf dem Kreis, denn er besitzt den Abstand
Der Punkt erfüllt also nicht die Kreisgleichung.

Abbildung 9.3.6: Skizze (C)
Ein wichtiger, häufig auftretender Spezialfall eines Kreises ist derjenige, für den der Mittelpunkt dem Ursprung des Koordinatensystems entspricht. So wird beispielsweise durch die Kreisgleichung
ein Kreis vom Radius um den Ursprung beschrieben:

Abbildung 9.3.7: Skizze (C)
Ein weiterer Spezialfall hiervon ist der Kreis mit Radius um den Ursprung.

Abbildung 9.3.8: Skizze (C)
Dieser trägt die besondere Bezeichnung Einheitskreis und spielt eine besondere Rolle in der Trigonometrie (vgl.: Abschnitte 5.6 und 6.5).
Aufgabe 9.3.6
- Ein Kreis ist durch die Gleichung
gegeben. Sein Mittelpunkt ist und sein Radius lautet
und sein Radius lautet
 . Zeichnen Sie den Kreis.
. Zeichnen Sie den Kreis.
- Die Kreisgleichung des Kreises vom Radius um den Punkt lautet
 .
.
Entscheiden Sie jeweils, ob die angegebenen Punkte auf dem Kreis liegen. Markieren Sie diejenigen Punkte, die auf dem Kreis liegen.
Richtig  Falsch
Falsch

Der Ursprung Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

In den obigen Beispielen und Aufgaben ist erkennbar, dass das Ablesen des Mittelpunkts und des Radius eines Kreises aus seiner Gleichung relativ einfach ist, insofern die Gleichung genau in der Form
aus Infobox 9.3.4 gegeben ist. Deshalb spricht man hierbei auch von der Normalform der Kreisgleichung. Leider kommt es aber oft vor, dass die Kreisgleichung nicht in dieser einfachen Form vorliegt, sondern erst in einigen Rechenschritten umgeformt werden muss, um dann den Mittelpunkt und den Radius ablesen zu können. Das Vorgehen wird in dem folgenden Beispiel demonstriert.
Beispiel
9.3.7
Gegeben ist ein Kreis durch die Gleichung
Dieser Gleichung sieht man weder sofort an, dass es sich um eine Kreisgleichung handelt, noch sind sofort der Mittelpunkt und der Radius des Kreises ersichtlich. Man kann die Gleichung aber auf Normalform bringen, indem man sich der Methode der Quadratischen Ergänzung bedient. Diese wird hier auf die Terme mit und die Terme mit in obiger Kreisgleichung getrennt angewandt.
Für die Terme mit ergibt sich
und für die Terme mit ergibt sich
Somit folgt für die Kreisgleichung:
Somit ist die Kreisgleichung auf Normalform gebracht und der Mittelpunkt und der Radius können abgelesen werden:
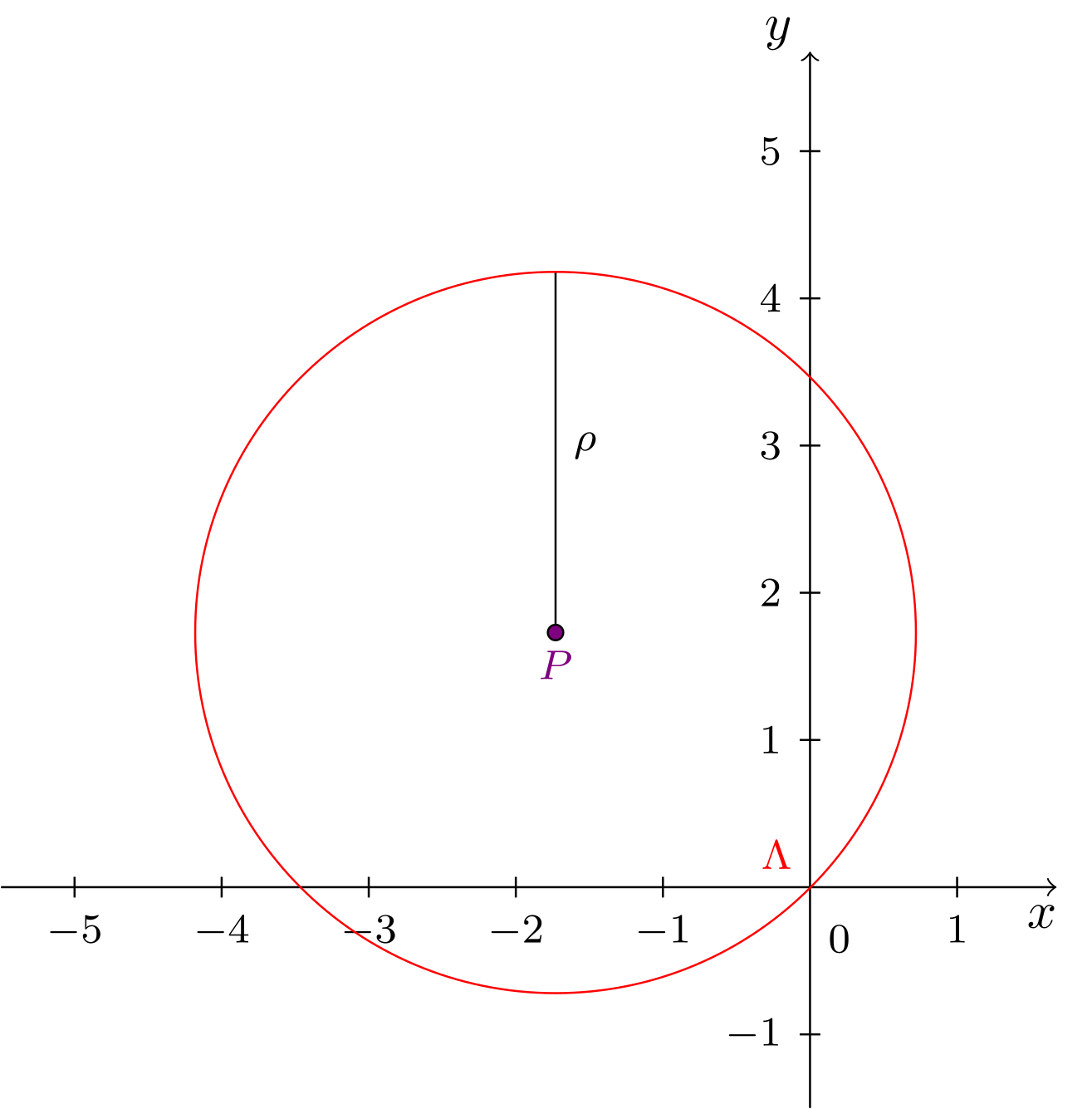
Gegeben ist ein Kreis durch die Gleichung
Dieser Gleichung sieht man weder sofort an, dass es sich um eine Kreisgleichung handelt, noch sind sofort der Mittelpunkt und der Radius des Kreises ersichtlich. Man kann die Gleichung aber auf Normalform bringen, indem man sich der Methode der Quadratischen Ergänzung bedient. Diese wird hier auf die Terme mit und die Terme mit in obiger Kreisgleichung getrennt angewandt.
Für die Terme mit ergibt sich
und für die Terme mit ergibt sich
Somit folgt für die Kreisgleichung:
Somit ist die Kreisgleichung auf Normalform gebracht und der Mittelpunkt und der Radius können abgelesen werden:

Abbildung 9.3.10: Skizze (C)
Aufgabe 9.3.8
Bestimmen Sie Mittelpunkt und Radius des Kreises
indem Sie die Kreisgleichung mittels Quadratischer Ergänzung auf Normalform bringen. Skizzieren Sie außerdem den Kreis.


Bestimmen Sie Mittelpunkt und Radius des Kreises
indem Sie die Kreisgleichung mittels Quadratischer Ergänzung auf Normalform bringen. Skizzieren Sie außerdem den Kreis.