2. Geometrie
  3. Winkelfunktionen: Sinus und Co.
  4. Einheitskreis

5.6.3 Trigonometrie am Einheitskreis



Im vorherigen Abschnitt wurden die trigonometrischen Funktionen anhand eines rechtwinkligen Dreiecks eingeführt. Die beschriebenen Eigenschaften gelten also für einen Winkelbereich von 0 ∘ bis 90 ∘ beziehungsweise 0 bis π 2 .

Um die gewonnenen Erkenntnisse auf größere Winkel als π/2 ausdehnen zu können, erweist sich der Blick auf den sogenannten Einheitskreis als besonders nützlich.

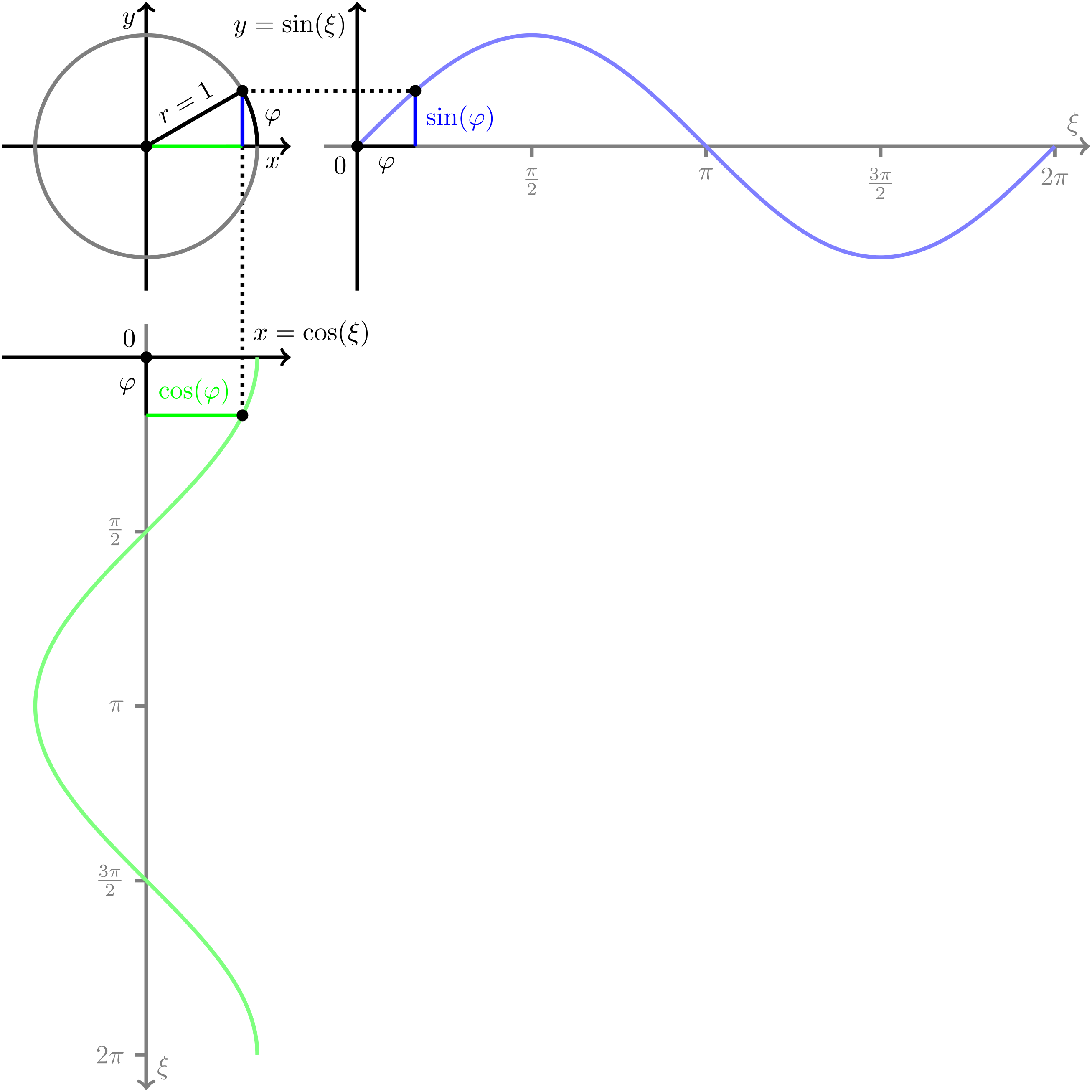
./_60CC3D36_4x.png
Abbildung 5.6.7: Skizze  (C)



Der Einheitskreis ist ein Kreis mit Radius 1. Sein Mittelpunkt wird im Nullpunkt eines kartesischen Koordinatensystems positioniert. Hier wird eine Strecke vom Mittelpunkt aus mit der Länge 1 betrachtet. Diese Strecke wird nun von ihrer horizontalen Ausgangslage auf der positiven x-Achse gegen den Uhrzeigersinn, also im mathematisch positiven Sinn, um den Nullpunkt gedreht. Dabei überstreicht ihr rotierendes Ende den Einheitskreis und bildet mit der positiven x-Achse den Winkel α, der bei der Rotation von 0 bis 2π bzw. 360 ∘ wächst. Zu jedem Winkel φ gehört also ein Punkt Pφ mit den Koordinaten xφ und yφ auf dem Einheitskreis.

Für φ zwischen 0 und π 2 kann man die Strecke, den zugehörigen Abschnitt auf der x-Achse und den zugehörigen y-Achsenabschnitt als rechtwinkliges Dreieck ansehen. Die Hypotenuse ist die Strecke mit der Länge 1, der x-Achsenabschnitt ist die Ankathete und der y-Achsenabschnitt die Gegenkathete. Dies entspricht der Situation aus dem vorherigen Abschnitt.

Der Sinus des Winkels φ ist also

sin(φ)= yφ 1 = yφ

und der Kosinus ist

cos(φ)= xφ 1 = xφ  .

Anhand der obigen Beschreibung am Einheitskreis gelten diese Definitionen jetzt auch für Winkel φ>π/2. Dabei können die Werte für xφ und yφ auch negativ werden und damit auch Sinus und Kosinus. Trägt man die y-Werte in Abhängigkeit vom Winkel φ in ein Diagramm ein, so erhält man die blaue Kurve für die Sinusfunktion. Für die x-Werte erhält man die grüne Kurve für die Kosinusfunktion. Indem man die Strecke in umgekehrter Richtung dreht, kann man entsprechend Werte für negative Winkel definieren.

Mit dem Satz von Pythagoras gilt außerdem

xφ 2 + yφ 2 =1 .

Setzt man hier die Beziehungen für xφ und yφ mit den Winkelfunktionen ein, so ergibt sich für beliebige Winkel φ die wichtige Beziehung

sin2 (φ)+ cos2 (φ)=1 .

Aus der Beschreibung von Sinus und Kosinus am Einheitskreis wird zudem ersichtlich, dass sich die Kosinuswerte bei Spiegelung an der x-Achse nicht ändern. Somit ist der Wert von cos zum Winkel φ gleich dem Kosinuswert zum Winkel -φ (in der Zeichnung grün dargestellt). Beim Sinus führt eine Spiegelung an der x-Achse zur Änderung des Vorzeichens des Sinuswertes (in der Zeichnung blau beziehungsweise violett dargestellt).

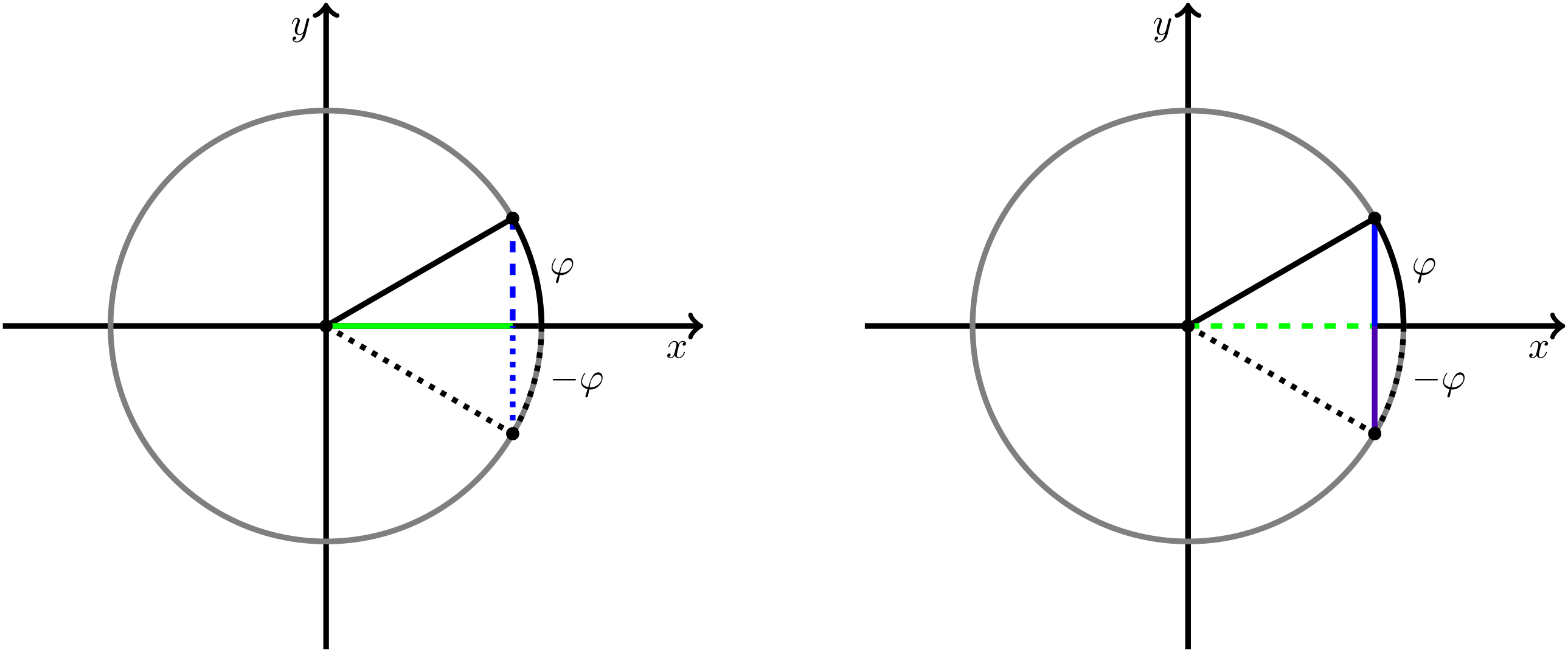
./_4339D0A6_4x.png
Abbildung 5.6.8: Skizze  (C)



Formelmäßig ausgedrückt bedeutet dies

cos(-φ)=cos(φ)       und       sin(-φ)=-sin(φ)

für jeden Winkel φ. Diese Symmetrieeigenschaften sind für viele Rechnungen hilfreich. Ein elementares Beispiel ist die Berechnung des Winkels zwischen x-Achse und der Verbindungsstrecke vom Nullpunkt zu einem Punkt im kartesischen Koordinatensystem (siehe auch Aufgabe 5.6.9).

Beispiel 5.6.8  
Gesucht sind jeweils die Werte des Sinus, Kosinus und Tangens des Winkels α=315 ∘ .

Für α=315 ∘ liegt der Punkt Pα im vierten Quadranten. Er wird auf dem Einheitskreis auch durch den negativen Winkel φ=315 ∘ -360 ∘ =-45 ∘ beschrieben. Damit ist sin(315 ∘ )=sin(-45 ∘ )=-sin(45 ∘ )=- 1 2 2 und cos(315 ∘ )=cos(-45 ∘ )=cos(45 ∘ )= 1 2 2 sowie tan(315 ∘ )=tan(-45 ∘ )=-1.