2. Elementare Funktionen
  3. Trigonometrische Funktionen
  4. Die Sinusfunktion

6.5.2 Die Sinusfunktion

In Modul 5 wurden die trigonometrischen Funktionen elementar im 5.6 über rechtwinklige Dreiecke durch

sin(α)= Gegenkathete Hypotenuse  .



sowie am Einheitskreis erklärt. Ausgehend von dieser Definition von sin(α) gelangt man zur Sinusfunktion, indem man den Winkel α zur Veränderlichen einer Funktion mit Namen sin macht. Man kann sich dies an Hand einer Familie von rechtwinkligen Dreiecken ABC verdeutlichen, die dem Einheitskreis, das ist ein Kreis mit Radius r=1, auf bestimmte Art und Weise einbeschrieben sind:



Beginnen wir mit dem Winkel α= 0∘ , also einem zur Strecke entarteten Dreieck, so ist die Länge der Strecke BC ‾ gleich 0. Lassen wir nun den Punkt B entgegen dem Uhrzeigersinn um den Kreis wandern, so wächst α - und auch sin(α) - zunächst an, bis für α= 90∘ ein maximaler Wert ( sin( 90∘ )=1) erreicht wird, bevor α weiter zu-, aber sin(α) wieder abnimmt. Für α= 180∘ ist das Dreieck ABC wieder zur Strecke degeneriert, und sin( 180∘ )=0. Wird α noch größer, „klappt“ das Dreieck „nach unten“, die Stecke BC ‾ ist parallel zur negativen Hochachse ( y-Achse) ausgerichtet, ihre Länge daher negativ. Für α= 270∘ tritt der maximal negative Wert auf, bevor er sich wieder 0 nähert. Bei α= 360∘ beginnt das Spiel von Neuem.
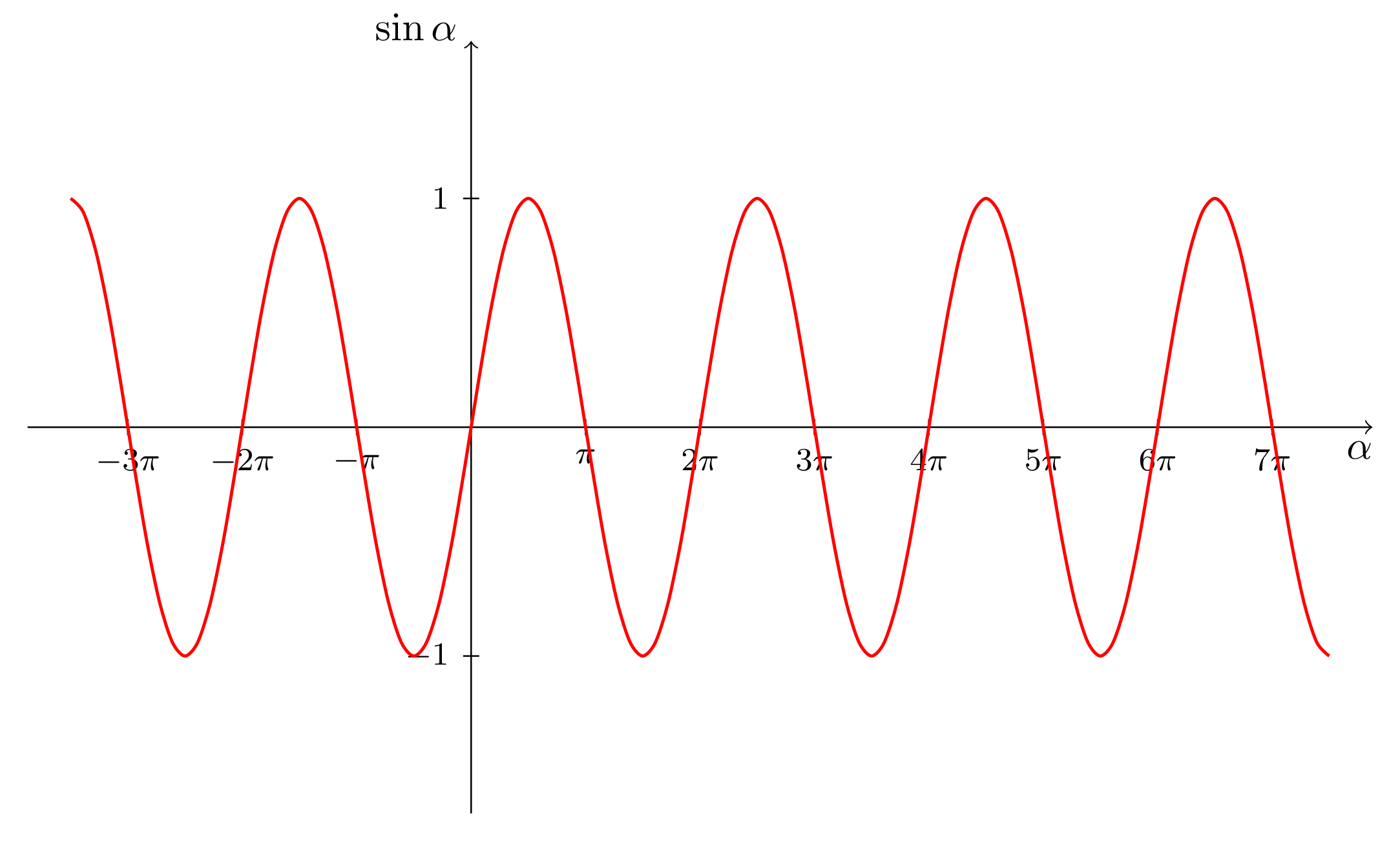
./_879BA9D9_4x.png
Abbildung 6.5.1: Skizze  (C)

Das voranstehende Schaubild gibt den Graphen der Sinusfunktion,

sin:ℝ→[-1;+1] α⟼sin(α) ,

wieder. Allerdings haben wir auf der Querachse ( α-Achse) den Winkel α nicht - wie in der bisherigen Diskussion - im Gradmaß aufgetragen, sondern wir haben das in diesem Zusammenhang üblichere Bogenmaß verwendet.

Halten wir einige der wichtigsten Eigenschaften der Sinusfunktion fest:
  • Die Sinusfunktion ist auf ganz ℝ definiert, Dsin =ℝ; der Wertebereich besteht dagegen nur aus dem Intervall von -1 bis +1, diese beiden Endpunkte eingeschlossen: Wsin =[-1;+1]

  • Nach gewissen Abständen wiederholt der Graph der Sinusfunktion exakt sein Aussehen; man spricht in diesem Zusammenhang von der Periodizität der Sinusfunktion. Die Periode beträgt 360∘ bzw. 2π. Formelmäßig kann man diesen Sachverhalt als

    sin(α)=sin(α+2π)

    ausdrücken.



Schon die Betrachtung des Graphen der einfachen Sinusfunktion legt die Verwendung dieser Funktion für die Beschreibung von Wellenvorgängen nahe. Um jedoch die gesamte Leistungsfähigkeit der Sinusfunktion ausschöpfen zu können, werden zuvor noch einige zusätzliche Parameter eingeführt. So können die „Ausschläge“ der Sinusfunktion mit einem sogenannten Amplitudenfaktor A verstärkt oder abgemildert, die „Schnelligkeit“ oder „Dichte“ der Auf- und Abbewegungen durch einen frequenzartigen Faktor a beeinflusst und der gesamte Verlauf des Graphen kann mit einer Verschiebekonstanten b nach rechts oder links verrückt werden. Die allgemeine Sinusfunktion besitzt daher folgende Gestalt:

f:ℝ→[-A;+A] x⟼f(x)=A sin(ax+b) .

Beispiel 6.5.1  
Beim Fadenpendel schwingt eine kleine schwere Masse im Gravitationsfeld der Erde an einem langen dünnen Faden, der z.B. fest an der Decke eines (hohen) Raumes verankert ist. Unter gewissen idealisierenden Annahmen und für kleine Werte des Auslenkwinkels φ aus der Ruhelage (der Lotrechten) hängt φ von der Veränderlichen t, der Zeit, über eine allgemeine Sinusfunktion ab:

φ(t)=A sin( 2π T t+b) .

Dabei bezeichnet T die sogenannte Schwingungsdauer des Pendels, also diejenige Zeitspanne, die für eine vollständige Schwingung vom Pendel benötigt wird.