10.2.1 Einführung
In diesem Abschnitt werden nun Vektoren genutzt, um (zunächst) Geraden in der Ebene zu beschreiben. Man stellt dann fest, dass sich diese Beschreibung von Geraden unmittelbar auf den dreidimensionalen Fall übertragen lässt, man also damit auch Geraden im Raum beschreiben kann. Im Raum gibt es dann, neben den Geraden, weitere mathematisch interessante und mit Hilfe von Vektoren einfach zu beschreibende Objekte, nämlich Ebenen. Schließlich kann man sich überlegen, wie Punkte, Geraden und Ebenen im Raum relativ zueinander liegen können.
Hierfür sind die - in der folgenden Infobox zusammengefassten - Konzepte wichtig.
Die folgenden Überlegungen und Abbildungen machen klar, warum die Konzepte der Kollinearität und Komplanarität insbesondere für die Betrachtung von Geraden und Ebenen wichtig sind:
Kollineare Vektoren sind Vielfache voneinander, das heißt die Repräsentanten kollinearer Vektoren mit gleichem Basispunkt liegen auf einer Geraden. Zum Beispiel sind die Vektoren
und
kollinear, da
(oder auch ) gilt. Weitere Vektoren die zu und auch zu kollinear sind, sind beispielsweise oder . Allerdings ist zum Beispiel der Vektor nicht kollinear zu (und damit auch nicht zu ), da es keine Zahl gibt, die die Gleichung
erfüllt. Repräsentanten kollinearer Vektoren mit gleichem Basispunkt, etwa die Pfeile der zugehörigen Ortsvektoren (siehe unten), liegen alle auf einer Geraden:
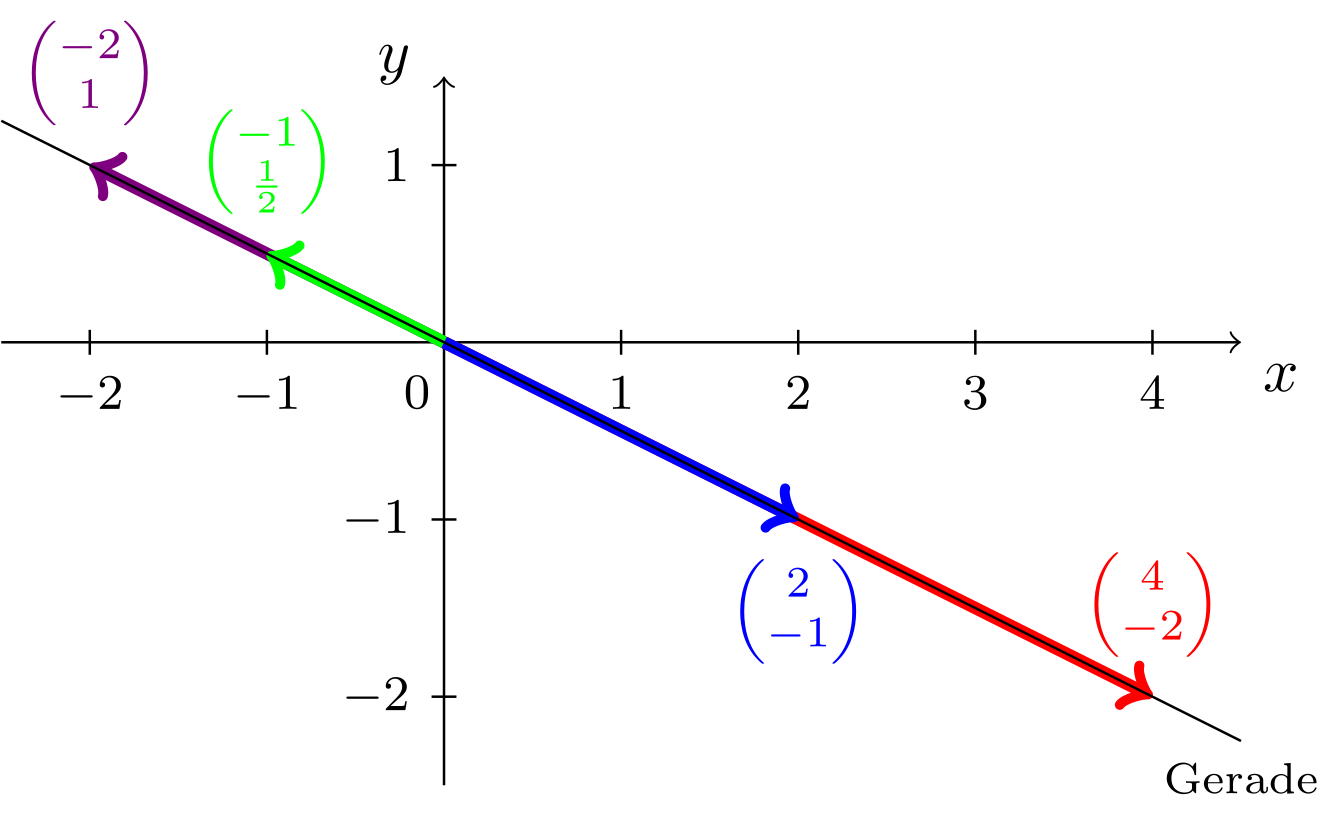
Komplanare Vektoren im Raum sind derart, dass ihre Repräsentanten in der gleichen Ebene liegen, falls diese den gleichen Basispunkt haben. So sind beispielsweise die Vektoren
komplanar, da
gilt. Die Pfeile ihrer zugehörigen Ortsvektoren als Repräsentanten liegen alle in der -Ebene eines Koordinatensystems im Raum. Dahingegen sind beispielsweise die Vektoren
nicht komplanar, da eine von Null verschiedene -Komponente aufweist, seine Repräsentanten also immer aus der -Ebene herauszeigen. Man sieht leicht ein, dass es keine Zahlen geben kann, so dass die Gleichung
erfüllt ist. Bild dazu:
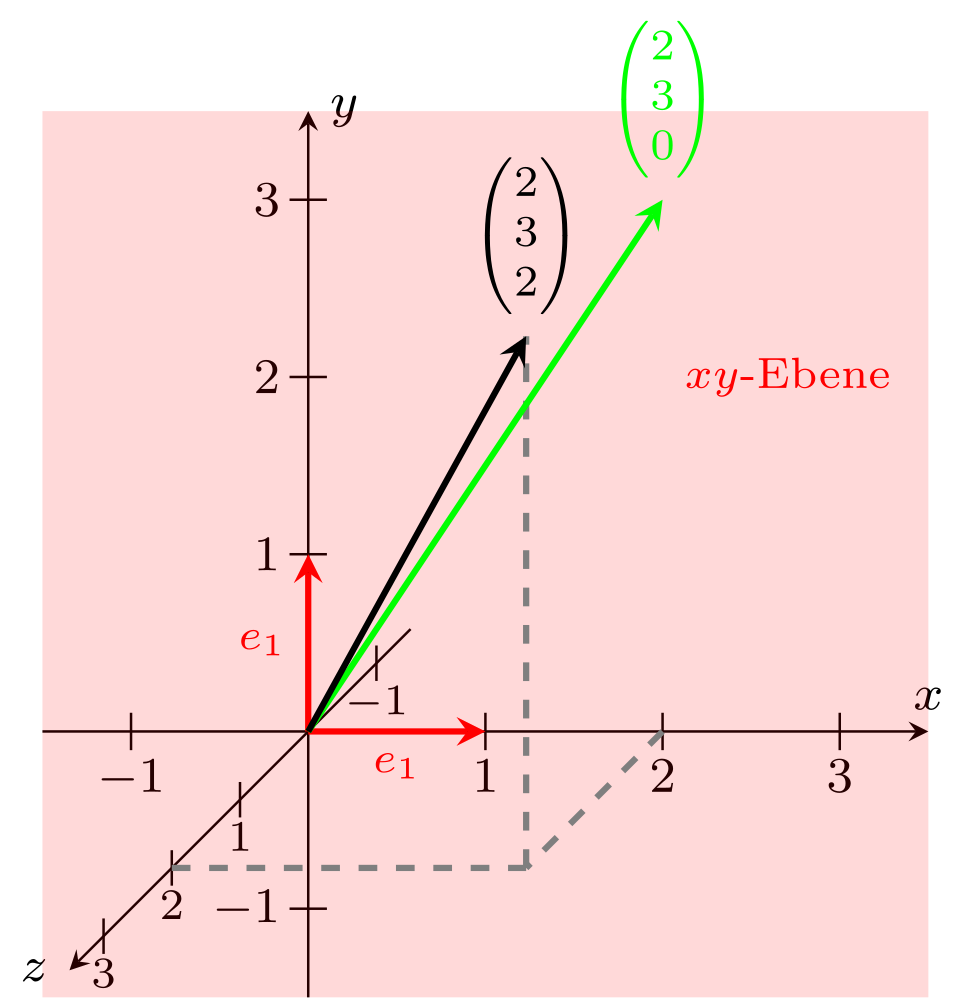
Hierfür sind die - in der folgenden Infobox zusammengefassten - Konzepte wichtig.
Die folgenden Überlegungen und Abbildungen machen klar, warum die Konzepte der Kollinearität und Komplanarität insbesondere für die Betrachtung von Geraden und Ebenen wichtig sind:
Kollineare Vektoren sind Vielfache voneinander, das heißt die Repräsentanten kollinearer Vektoren mit gleichem Basispunkt liegen auf einer Geraden. Zum Beispiel sind die Vektoren
und
kollinear, da
(oder auch ) gilt. Weitere Vektoren die zu und auch zu kollinear sind, sind beispielsweise oder . Allerdings ist zum Beispiel der Vektor nicht kollinear zu (und damit auch nicht zu ), da es keine Zahl gibt, die die Gleichung
erfüllt. Repräsentanten kollinearer Vektoren mit gleichem Basispunkt, etwa die Pfeile der zugehörigen Ortsvektoren (siehe unten), liegen alle auf einer Geraden:

Abbildung 10.2.1: Skizze (C)
komplanar, da
gilt. Die Pfeile ihrer zugehörigen Ortsvektoren als Repräsentanten liegen alle in der -Ebene eines Koordinatensystems im Raum. Dahingegen sind beispielsweise die Vektoren
nicht komplanar, da eine von Null verschiedene -Komponente aufweist, seine Repräsentanten also immer aus der -Ebene herauszeigen. Man sieht leicht ein, dass es keine Zahlen geben kann, so dass die Gleichung
erfüllt ist. Bild dazu:

Abbildung 10.2.2: Skizze (C)


