2. Geometrie
  3. Grundbegriffe der ebenen Geometrie
  4. Punkte und Geraden

5.1.2 Punkte und Geraden



Ein Standpunkt oder eine Position in einer Ebene wird in der Geometrie zum einfachsten Objekt, einem Punkt, idealisiert. Über einen einzelnen Punkten lässt sich nichts weiter sagen.

Betrachtet man mehrere Punkte, kann man auf verschiedene Weise Beziehungen zwischen den Punkten betrachten - und man kann neue Objekte wie zum Beispiel Strecken und Geraden beschreiben (siehe die folgende Abbildung). Mathematisch gesprochen, sind es Mengen von Punkten.

./_BFFBCBAD_4x.png
Abbildung 5.1.2: Skizze  (C)



Als Erstes wird eine Strecke und der Abstand zwischen Punkten betrachtet. Dazu bedarf es noch eines Vergleichsmaßstabs, um den Abstand messen zu können. In der Mathematik wird dazu eine Vergleichsstecke ausgewählt, deren Länge als Einheitslänge bezeichnet wird. Für Anwendungen wird man entsprechend der Aufgabe passende Einheiten wie zum Beispiel Meter oder Zentimeter als Längeneinheit festlegen.

Strecken und Abstände 5.1.1  
Gegeben sind Punkte A und B. Die Strecke AB ‾ zwischen A und B ist der kürzeste Weg zwischen den Punkten A und B.

./_D730F529_4x.png
Abbildung 5.1.3: Skizze  (C)



Die Länge der Strecke AB ‾ wird mit [ AB ‾ ] notiert. Die Streckenlänge ist gleich dem Abstand zwischen den Punkten A und B.


Das Bild von einem Lichtstrahl, ausgesandt von einem fernen Stern oder von der Sonne, ist eine passende Vorstellung für einen Strahl, der in einem Punkt A beginnt und in Richtung eines zweiten Punktes B gedanklich immer weiter geht. Ein Strahl wird auch Halbgerade genannt.

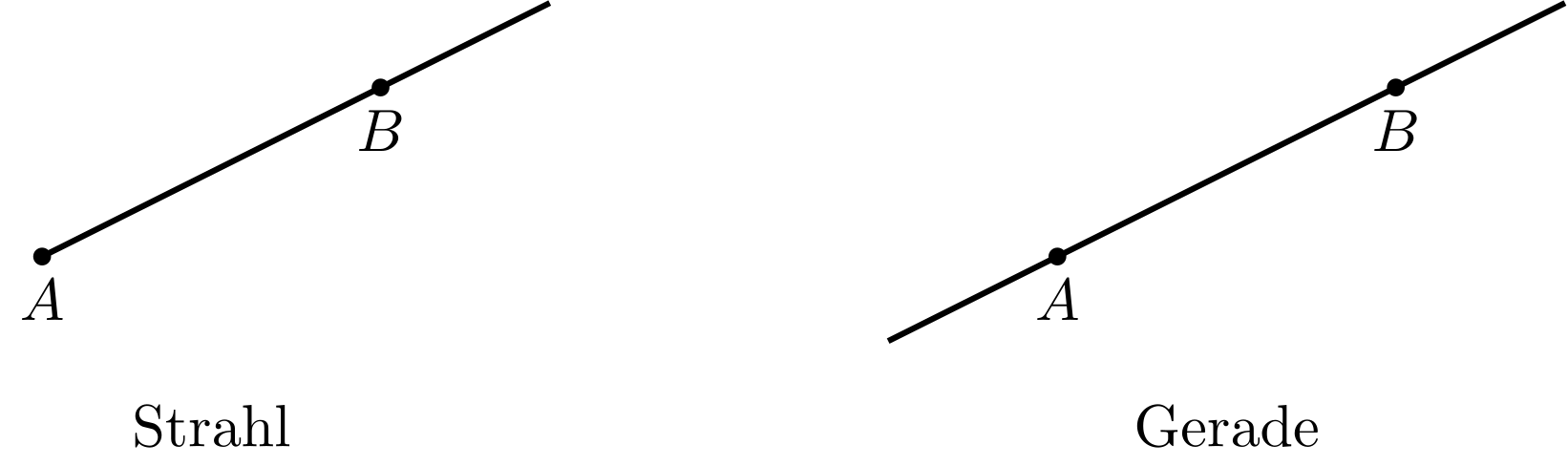
./_CBE87BD3_4x.png
Abbildung 5.1.4: Skizze  (C)



Wenn man den Weg auf einer Strecke AB ‾ in beide Richtungen fortsetzt, spricht man von einer Geraden.

Gerade 5.1.2  
Seien A und B zwei Punkte (das heißt, es ist A ein Punkt, der vom Punkt B verschieden ist). Dann bestimmen A und B genau eine Gerade AB.
Wenn man zu zwei Punkten A und B einen weiteren Punkt P betrachtet, kann man nach dem Abstand d von P zur Geraden AB fragen. Dies ist die kleinste Entfernung zwischen P und den Punkten der Geraden AB.

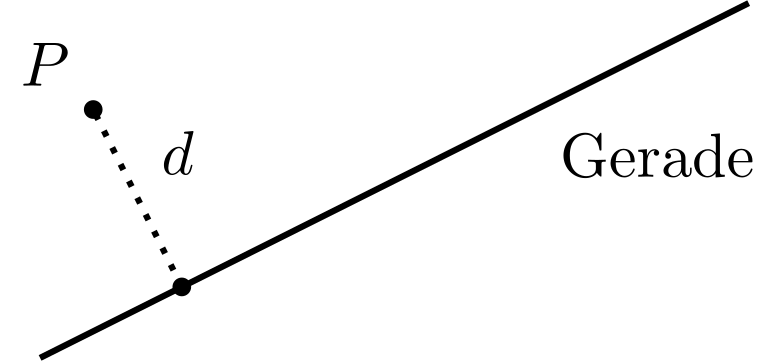
./_28009FFF_4x.png
Abbildung 5.1.5: Skizze  (C)



Wenn drei Punkte P, Q und S in der Ebene betrachtet werden, sind damit Geraden SP und SQ festgelegt.

Sie haben den Punkt S gemeinsam. Liegt auch der Punkt Q auf der Geraden SP, dann bezeichnen SQ und SP dieselbe Gerade. Wenn Q nicht zur Geraden SP gehört, sind SQ und SP verschiedene Geraden. Die beiden Geraden haben nur den Punkt S, den Schnittpunkt, gemeinsam.

Für irgendwelche Geraden g und h gibt es noch den Fall, dass sie keinen Punkt gemeinsam haben. Der kleinste Abstand von Punkten auf g beziehungsweise h ist der Abstand zwischen den Geraden g und h. Somit haben g und h keinen gemeinsamen Punkt, wenn ihr Abstand größer als 0 ist. Geraden heißen parallel, wenn jeder Punkt auf einer der Geraden denselben Abstand zur anderen Geraden hat.

Auch eine einzelne Gerade kann über den Abstand von zwei Punkten M und M' beschrieben werden: Die Menge aller Punkte, die von zwei Punkten M und M' gleich weit entfernt sind, ist eine Gerade.

Dies ist eine typische Vorgehensweise in der Geometrie, mit Hilfe von Eigenschaften wie einem Abstand neue Objekte zu definieren. Auf diese Weise kann auch ein Kreis ganz einfach beschrieben werden.

Kreis 5.1.3  
Gegeben ist ein Punkt M und eine positive reelle Zahl r.

Dann heißt die Menge aller Punkte, die von M den Abstand r haben, ein Kreis um M mit Radius r.
./_FFD36667_4x.png
Abbildung 5.1.6: Skizze  (C)