2. Geometrie
  3. Elementargeometrische Körper
  4. Elementargeometrische Körper

5.5.2 Elementargeometrische Körper



Punkte sind die einfachsten grundlegenden geometrischen Objekte. Verschiebungen führen auf Strecken, und Operationen wie das Verschieben oder Drehen von Strecken in der Ebene führen auf elementargeometrische Figuren. Beispielsweise ergeben sich Vielecke und Kreise, wie sie oben beschrieben wurden.

Wenn man Figuren außerhalb ihrer Ebene verschiebt oder dreht, entstehen neue Objekte, die als Körper bezeichnet werden. Im Folgenden werden einige einfache Körper beschrieben, deren Form in vielen alltäglichen Gegenständen oder technischen Konstruktionen erkennbar ist.

Beispiel 5.5.1  
Es wird ein Rechteck betrachtet und senkrecht zur Zeichenebene verschoben. Dadurch entsteht ein Quader. Seine Oberfläche besteht aus dem gegebenen Rechteck und einer Kopie davon. Außerdem entstanden aus den vier Seiten des ursprünglichen Rechtecks jeweils vier weitere Rechtecke.


Betrachtet man irgend ein Vieleck und verschiebt dieses senkrecht, entsteht ein Prisma genannter Körper. Der Name wird auch für durchsichtige physikalische Körper dieser Form verwendet, mit denen Lichtwellen gebrochen werden. Die einzelnen Lichtwellen von scheinbar weißem Licht werden in verschiedenen Farben sichtbar.

Prisma 5.5.2  
Gegeben ist ein Vieleck G. Ein Prisma ist ein Körper, der aus einer senkrechten Verschiebung eines Vielecks G um eine Strecke der Länge h entsteht. Die beiden Flächen, die aus dem gegebenen Vieleck und einer Kopie einen Teil der Oberfläche bilden, werden dann als Grundfläche des Prismas bezeichnet. Sie sind zueinander parallel. Die anderen Flächen bilden zusammen den Mantel M.

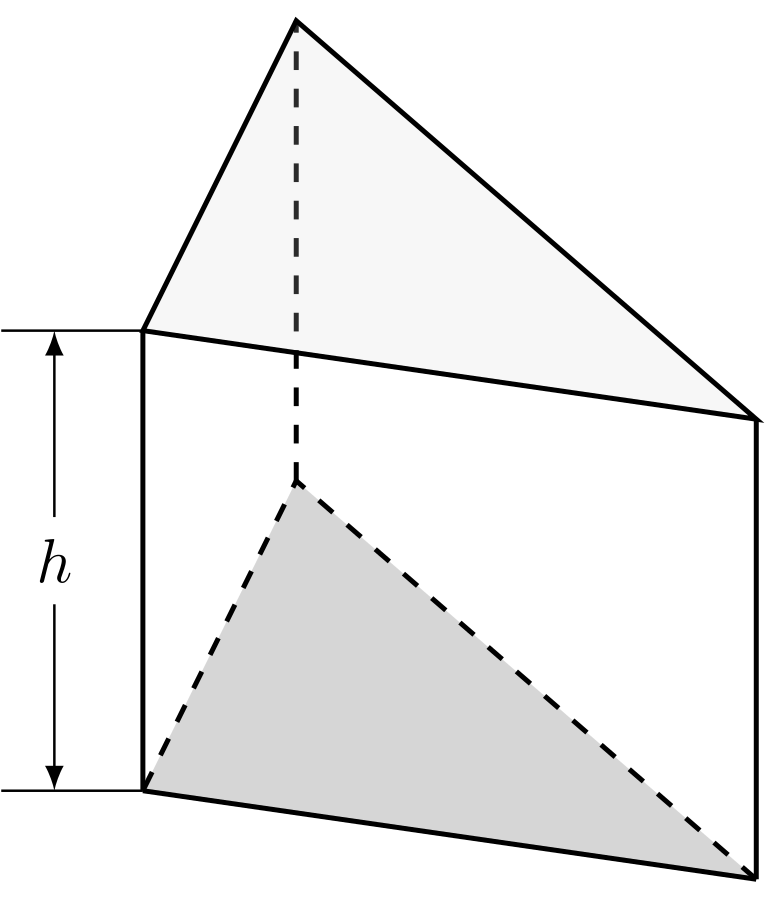
./_689D7FEE_4x.png
Abbildung 5.5.1: Skizze  (C)



In der Zeichnung ist ein Prisma mit einem Dreieck als Grundfläche gezeigt. Die anderen Seitenflächen, die an die Grundfläche angrenzen, sind Rechtecke.

Das Volumen V des Prismas ist das Produkt aus dem Flächeninhalt des Vielecks G und der Höhe h: Es ist V=G·h.

Der Flächeninhalt O der Oberfläche ergibt sich aus dem doppelten Inhalt der Grundfläche G und dem Flächeninhalt des Mantels M. Wenn U der Umfang des gegebenen Vielecks ist, gilt O=2·G+M=2·G+U·h.


Im einführenden Beispiel wurde ein Quader beschrieben. Mit obiger Definition kann er als spezielles Prisma angesehen werden, nämlich als ein Prisma mit einem Rechteck als Grundfläche. Wenn alle Seitenflächen Quadrate sind, spricht man von einem Würfel.

Das Bauprinzip kann auf verschiedene Weisen variiert werden. Beispielsweise kann das Vieleck durch eine Kreisscheibe ersetzt werden, die verschoben wird. Durch die senkrechte Verschiebung entsteht ein besonders symmetrischer Körper, ein Zylinder. Eine Tunnelbohrmaschine stellt - vereinfacht - eine zylinderförmige Röhre her.

Zylinder 5.5.3  
Gegeben ist eine Kreisscheibe G. Ein Zylinder ist ein Körper, der aus einer senkrechten Verschiebung einer Kreisscheibe G um eine Strecke der Länge h entsteht. Die beiden Flächen, die aus der gegebenen Kreisscheibe und einer Kopie einen Teil der Oberfläche bilden, werden dann als Grundfläche des Zylinders bezeichnet. Sie sind zueinander parallel. Der gekrümmte Teil der Oberfläche zwischen den beiden Kreisscheiben bildet den Mantel M des Zylinders.

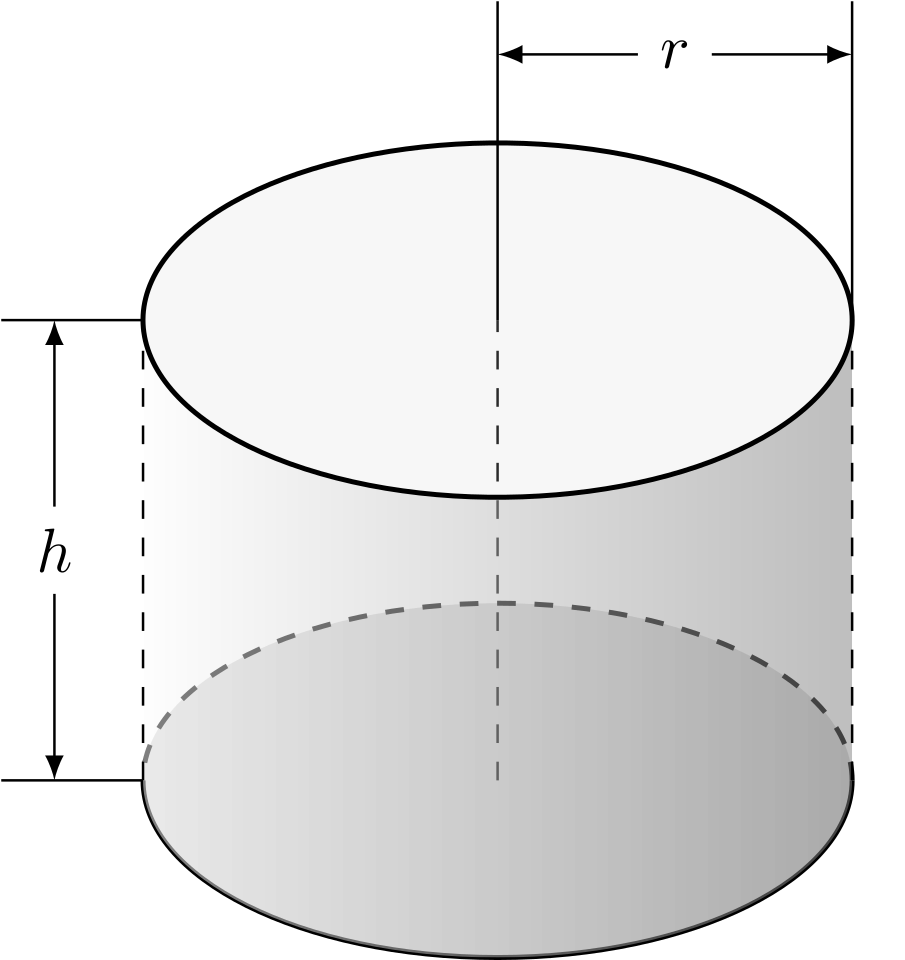
./_F03C68D7_4x.png
Abbildung 5.5.2: Skizze  (C)



Das Volumen V des Zylinders ist das Produkt aus dem Flächeninhalt der Kreisscheibe G mit dem Radius r und der Höhe h: Es ist V=G·h=π· r2 ·h.

Der Flächeninhalt O der Oberfläche ergibt sich als Summe aus dem doppelten Inhalt der Kreisscheibe G und dem Inhalt des Mantels M. Mit dem Umfang U=2·π·r der gegebenen Kreisscheibe gilt O=2·G+M=2·π· r2 +2·π·r·h=2·π·r·(r+h).


Wenn die Kreisscheibe nicht verschoben, sondern rotiert wird, wobei die Drehachse durch den Mittelpunkt und einen Randpunkt verläuft, ergibt sich eine Kugel.

Kugel 5.5.4  
Gegeben ist eine Kreisscheibe mit Mittelpunkt M und Radius r. Rotiert die Kreisscheibe um M und einen Randpunkt, erhält man eine Kugel mit Radius r.

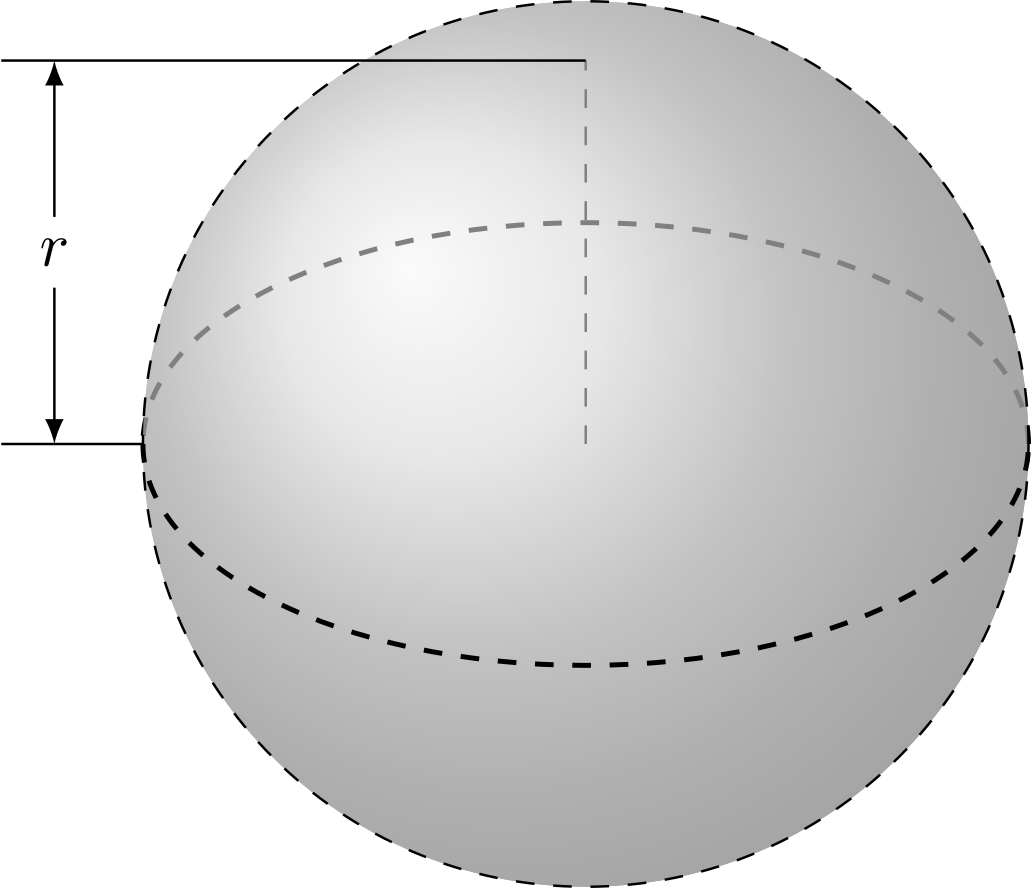
./_63234011_4x.png
Abbildung 5.5.3: Skizze  (C)



Das Volumen V der Kugel ist V= 4 3 ·π· r3 .

Der Flächeninhalt O der Oberfläche ist durch O=4·π· r2 gegeben.


Eine Kugel kann auch als der Körper beschrieben werden, der aus allen Punkten besteht, deren Abstand von M kleiner oder gleich r ist (siehe auch Kapitel 10).

In dieser Betrachtungsweise ist ein Prisma ein Körper aus allen Punkten, die auf einer Verbindungslinie von Grundfläche und ihrer Kopie liegen.

Im Folgenden werden zwei Variationen dieses Vorgehens betrachtet. Zunächst wird wieder von einem Vieleck als Grundfläche ausgegangen. Anstelle einer Kopie der Grundfläche wird jetzt nur ein einzelner Punkt vorgegeben.

Pyramide 5.5.5  
Gegeben ist ein Vieleck G und ein Punkt S mit dem Abstand h>0 von G. Eine Pyramide mit der Grundfläche G und der Spitze S ist der Körper, der aus allen Punkten besteht, die auf einer Strecke von S zu einem Punkt auf der Grundfläche G liegen.

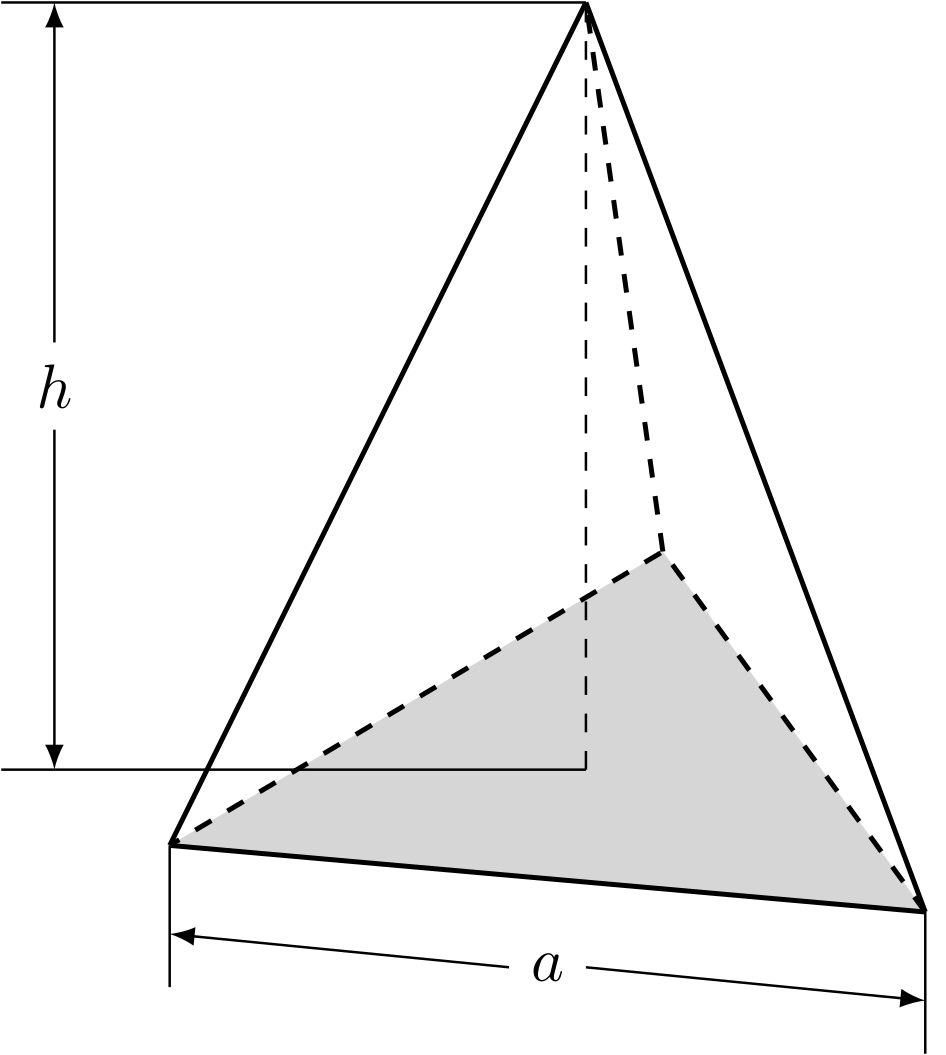
./_83C6F22A_4x.png
Abbildung 5.5.4: Skizze  (C)



In der Zeichnung ist eine Pyramide mit einer dreieckigen Grundfläche dargestellt.

Das Volumen V der Pyramide ist proportional zum Flächeninhalt der Grundfläche G und der Höhe h. Es gilt V= 1 3 ·G·h.

Der Flächeninhalt O der Oberfläche ergibt sich als Summe aus dem Inhalt der Grundfläche G und des Mantels M. Dabei ist der Flächeninhalt des Mantels die Summe seiner Dreiecksflächen Dk ( 1≤k≤n). Damit ist O=G+M=G+ D1 +…+ Dn .


In besonderen Situationen ergeben sich einfache Formeln, mit denen das Volumen und die Oberfläche berechnet werden können. Ein Beispiel ist die oben abgebildete Pyramide. Dort ist die Grundfläche ein gleichseitiges Dreieck. Die folgende Aufgabe bietet die Gelegenheit, für einen speziellen Fall dieser Situation eine Formel für die Oberfläche mit den Eigenschaften gleichseitiger Dreiecke zu finden.

Aufgabe 5.5.6  
Berechnen Sie die Oberfläche O einer Pyramide, deren Seiten alle gleichseitige Dreiecke mit der Seitenlänge a sind.

Antwort: O  = 



Die Überlegungen von oben, dass Prismen und Zylinder ein gemeinsames Bauprinzip bei unterschiedlichen Grundflächen haben, kann auf die neue Situation einer Pyramide übertragen werden. Man erhält einen weiteren Körper, wenn anstatt eines Vielecks wie bei der Pyramide eine Kreisscheibe als Grundfläche verwendet wird.

Kegel 5.5.7  
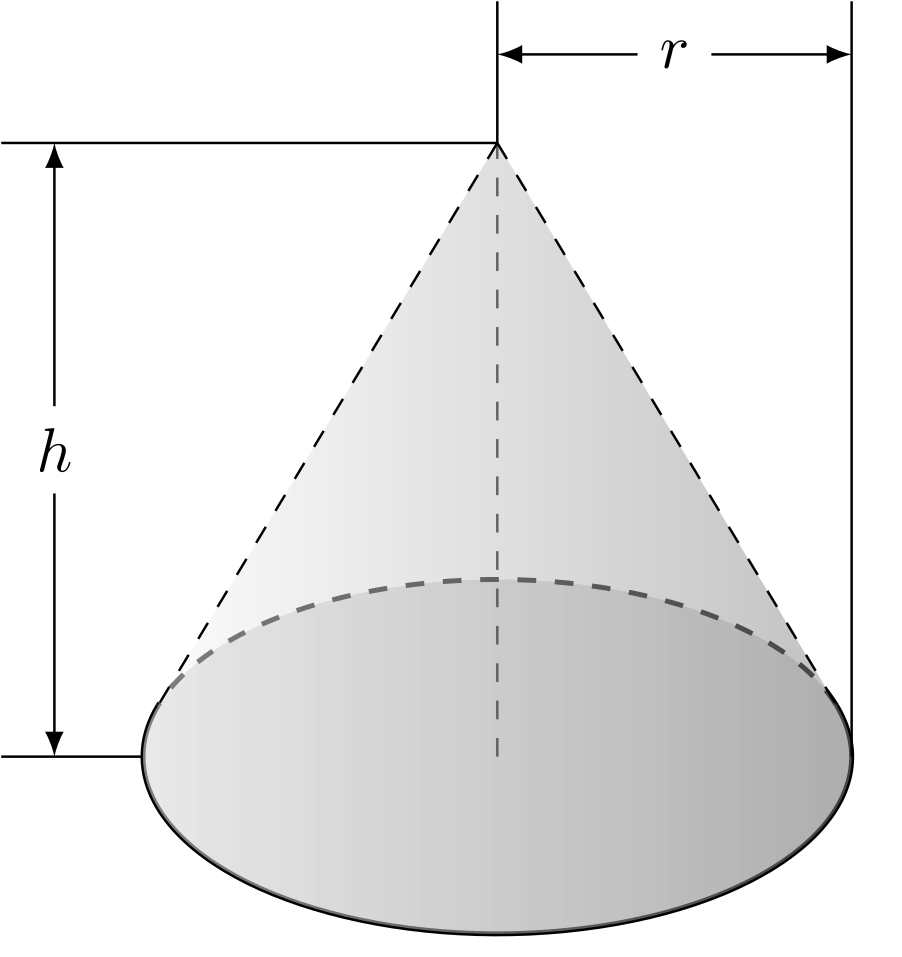
Gegeben ist eine Kreisscheibe G mit Radius r. Außerdem wird ein Punkt S mit dem Abstand h>0 von G betrachtet. Ein Kegel mit der Grundfläche G und der Spitze S ist der Körper, der aus allen Punkten besteht, die auf einer Strecke von S zu einem Punkt auf der Grundfläche G liegen.

./_1BD514D3_4x.png
Abbildung 5.5.5: Skizze  (C)



Das Volumen V des Kegels ist proportional zum Flächeninhalt der Kreisscheibe G und der Höhe h. Es gilt V= 1 3 ·G·h= 1 3 ·π· r2 ·h.

Ein Kegel in der hier betrachteten Situation, in der sich die Spitze des Kegels senkrecht über dem Mittelpunkt der Kreisscheibe befindet, wird genauer als gerader Kreiskegel bezeichnet.

Der Flächeninhalt der Oberfläche eines geraden Kreiskegels ist die Summe des Inhalts der Kreisscheibe G und des Mantels M. Wenn ℓ der Abstand der Kegelspitze vom Rand der Kreisscheibe ist, gilt mit dem Kreisumfang U=2πr dann O=G+M=π· r2 +π·r·ℓ=π·r·(r+ℓ).


In obiger Zeichnung eines Kegels wird die Höhe h genannt. Die angebenen Formeln enthalten jedoch den Abstand der Spitze vom Rand der Kreisscheibe. Wie hängen beide Größen zusammen?

Aufgabe 5.5.8  
Stellen Sie sich vor, der gerade Kegel wird von der Spitze eben durch den Mittelpunkt der Kreisscheibe in zwei gleiche Teile zerlegt. Dann ist eine Seite der beiden Teile jeweils ein Dreieck, durch dessen Seiten die Höhe h, der Abstand ℓ und der Radius r beziehungsweise der Durchmesser der Kreisscheibe bestimmt werden. Hierbei werden r und h als gegeben angesehen.

  1. Beschreiben Sie ℓ in Abhängigkeit von h und r:

    ℓ  = 



  2. Geben Sie die Oberfläche O des Kegels in Abhängigkeit von h und r an:

    O  =