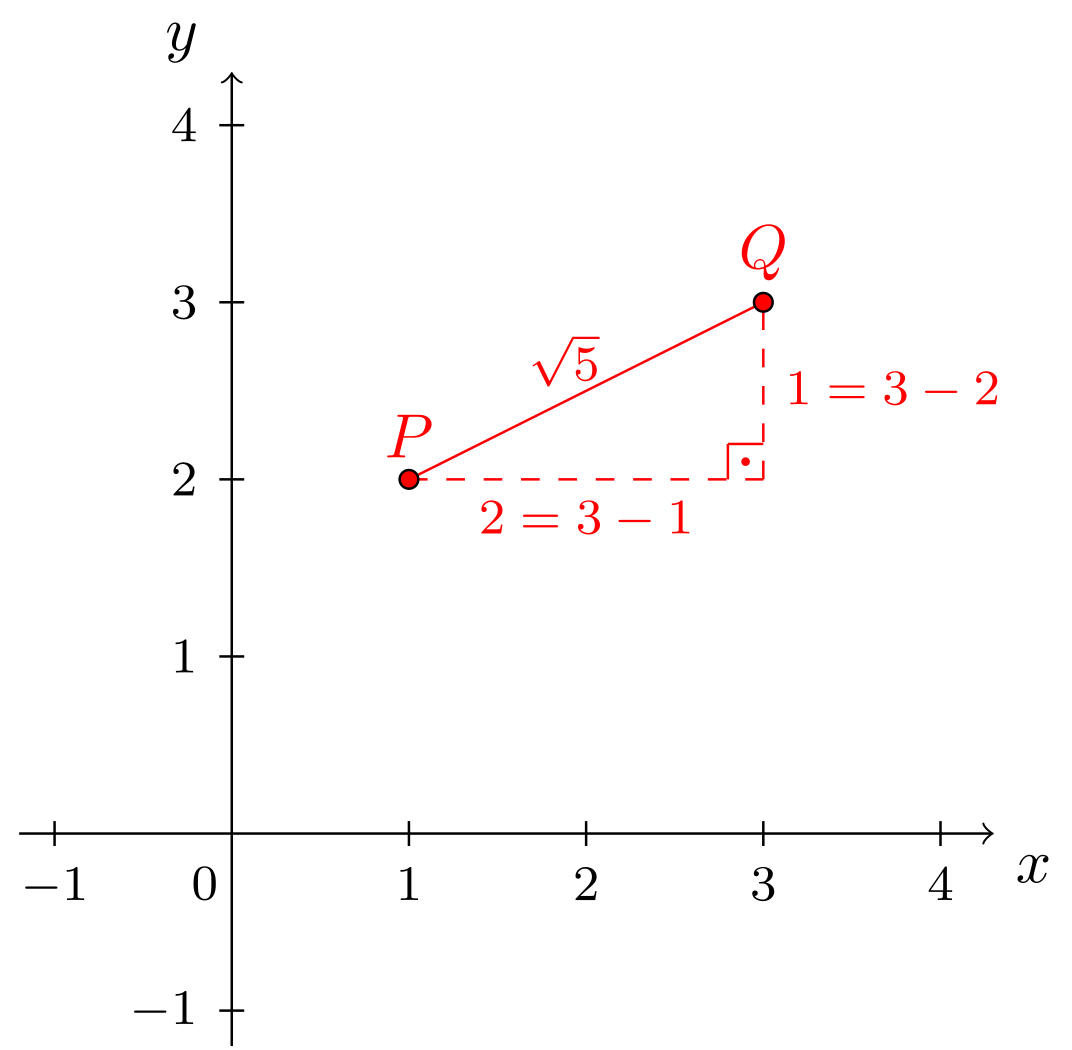2. Orientierung im zweidimensionalen Koordinatensystem
  3. Kreise in der Ebene
  4. Abstand Strecken

9.3.2 Abstand und Streckenlänge



Rekapituliert man nochmals das einführende Beispiel des Hydranten aus 9.1.1, so stellt man fest, dass man mit Hilfe der Daten auf dem Hydrantenschild zwar nun den Ort des Hydranten in einem Koordinatensystem genau angeben kann. Interessiert man sich aber dafür, wie weit der Hydrant vom Schild tatsächlich entfernt ist, muss man dies aus den Koordinaten erst ausrechnen.

./hydrant.png


Hier hilft der Satz des Pythagoras weiter:

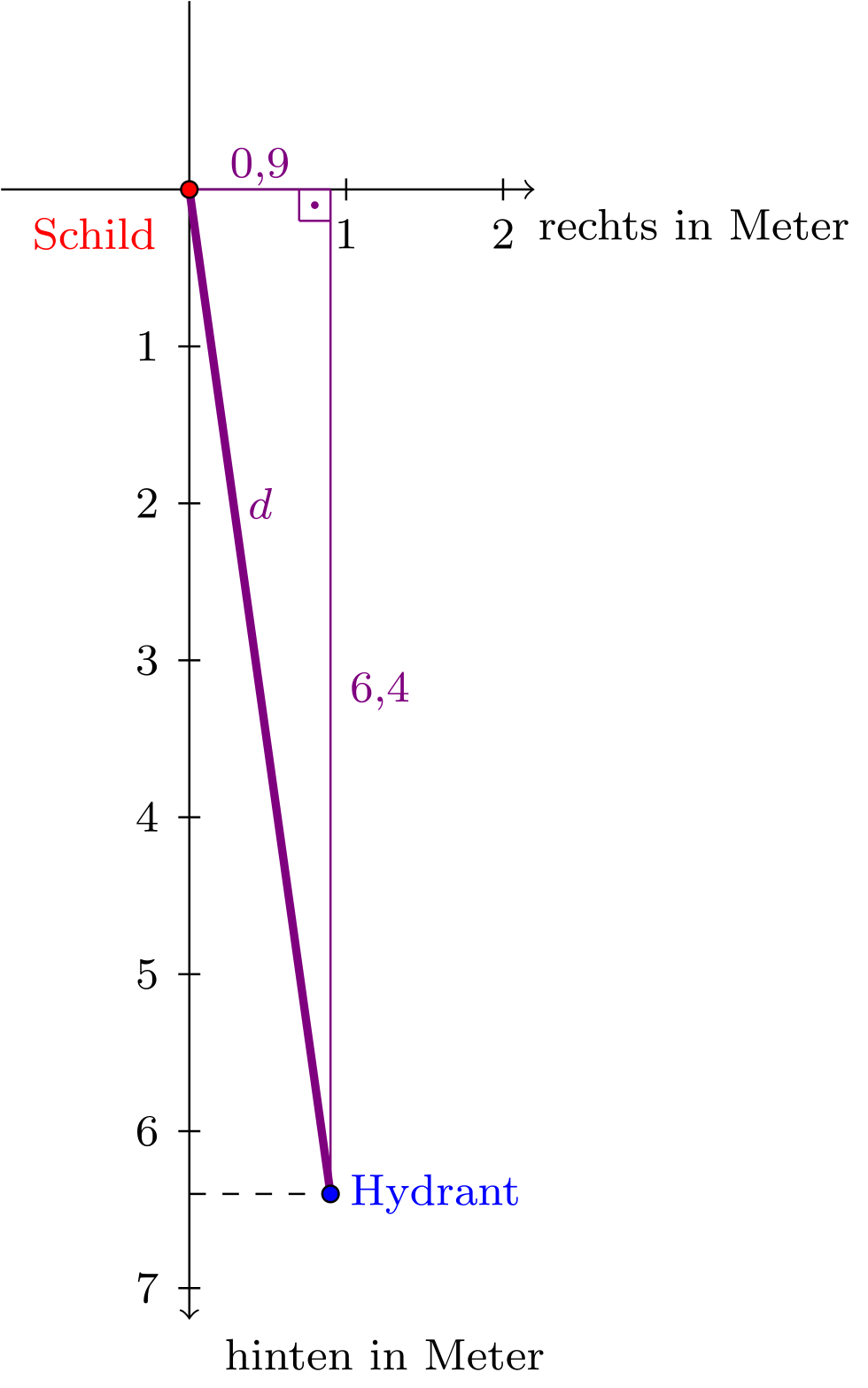
./_D826A992_4x.png
Abbildung 9.3.3: Skizze  (C)



Man erhält für den Abstand d zwischen Schild und Hydrant:

d2 =0,92 +6,42  .

Somit kann man d hier (näherungsweise) ausrechnen:

d=0,81+40,96≈6,46 .

Der Abstand zwischen Schild und Hydrant beträgt also (in der hier verwendeten Längeneinheit Meter) etwa 6 Meter und 46 Zentimeter. Für rein mathematische Betrachtungen sind auch hier die Längeneinheiten nicht wichtig, so dass diese im Folgenden wieder weggelassen werden.

Das obige Beispiel des Schilds und des Hydranten kann man bequem verallgemeinern. Der Abstand zwischen zwei Punkten im ℝ2 ist stets durch das Anlegen eines geeigneten rechtwinkligen Dreiecks und durch den Satz des Pythagoras zu bestimmen.

Beispiel 9.3.1  
Die Punkte P=(1;2) und Q=(3;3) haben den Abstand

(3-1 )2 +(3-2 )2 = 22 + 12 =5 .

./_F7C506A4_4x.png
Abbildung 9.3.4: Skizze  (C)



Der Abstand zwischen zwei Punkten in der Ebene kann also dadurch berechnet werden, dass man aus ihren Abszissen und Ordinaten die Seitenlängen eines rechtwinkligen Dreiecks bestimmt und dann den Satz des Pythagoras anwendet. Weiterhin ist in obigem Beispiel 9.3.1 ersichtlich, dass der Abstand zwischen den Punkten P und Q genau die Länge eines endlichen Stücks der Gerade PQ beschreibt, nämlich desjenigen Stücks zwischen P und Q. Dieses endliche Stück der Gerade PQ heißt Strecke zwischen P und Q und wird mit dem Symbol PQ ‾ bezeichnet. Die Länge der Strecke PQ ‾ ist der Abstand zwischen P und Q und trägt das Symbol [ PQ ‾ ].

Info 9.3.2  
 
Der Abstand zwischen zwei Punkten P=( x0 ; y0 ) und Q=( x1 ; y1 ) im ℝ2 ist gegeben durch

[ PQ ‾ ]=( x1 - x0 )2 +( y1 - y0 )2  .



Man stellt hier außerdem fest: zwei Punkte haben genau dann den Abstand Null, wenn sie identisch sind.

Aufgabe 9.3.3  
  1. Berechnen Sie den Abstand der beiden Punkte A=(-1;-5) und B=(4;7).
    [ AB ‾ ]=

  2. Berechnen Sie das Quadrat des Abstands der beiden Punkte P=(3;0) und Q=(1;ψ) in Abhängigkeit von ψ.
    [ PQ ‾ ]2  = 

  3. Bestimmen Sie den Punkt V im III. Quadranten, der vom Punkt U=(2;1) den Abstand 35 hat und auf der Geraden durch U mit der Steigung 2 liegt.
    V  = 

Beim zweiten Aufgabenteil ist ψ eine unbekannte Konstante, die in der Lösung als psi eingegeben werden kann.