5.4.3 Vielecke
Bei Dreiecken trägt bereits eine Ecke oder Seite wesentlich zu den Eigenschaften des gesamten Dreiecks bei, zum Beispiel eine Ecke mit einem rechten Winkel. In Vierecken ist eine Ecke nicht mehr ganz so bestimmend. Dafür gibt es mehr Variationen der Formen. Wenn „viele“ Punkte durch Strecken zu einer geschlossenen Figur, einem Vieleck, verbunden werden, ergeben sich viele Möglichkeiten, vielfältige Flächen zu gestalten und sogar runde Formen anzunähern.
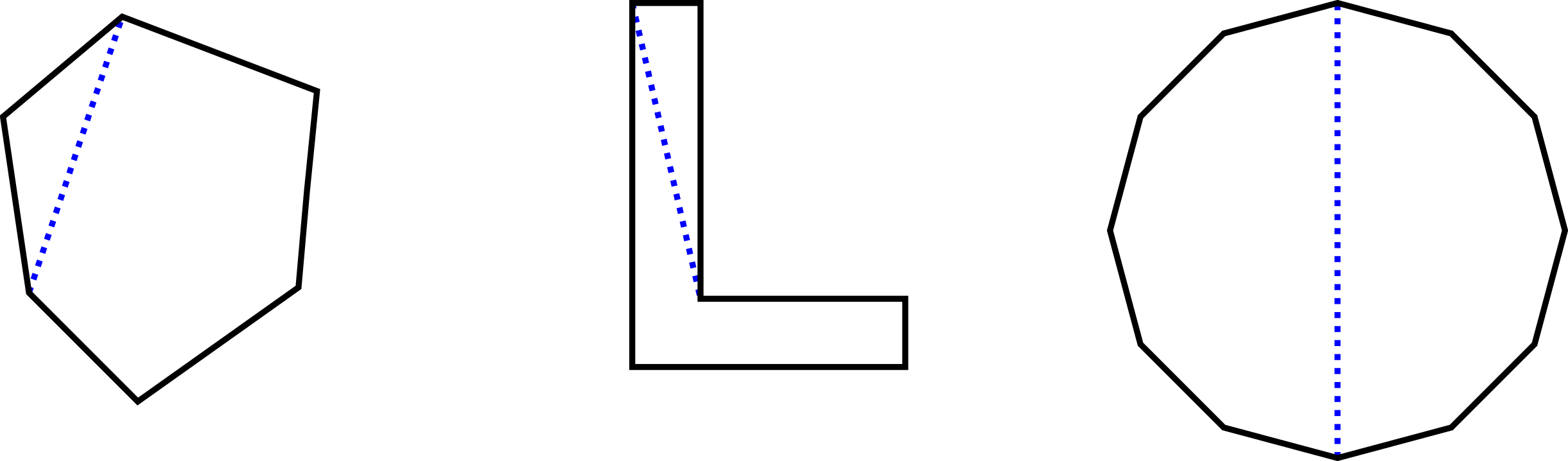
Abbildung 5.4.7: Skizze (C)
Eine so detaillierte Einteilung wie für Dreiecke oder Vierecke ist dabei kaum mehr möglich. Die neuen Möglichkeiten wie die Annäherung an runde Formen führen auch auf andere interessante Fragen. Dazu werden nicht einzelne Vielecke sondern Konstruktionsprinzipien für eine Abfolge von vielen Vielecken betrachtet. Und andererseits kann jedes Vieleck bei Bedarf in Dreiecke zerlegt werden, wie dies schon bei Vierecken beobachtet wurde. Eine Eigenschaft einer besonderen Ecke wird somit vielfach unter dem Aspekt betrachtet, was dies insgesamt für das Vieleck bedeutet.
Zur Einteilung in verschiedene Klassen bietet sich hier die Fragestellung an, ob eine gewisse Eigenschaft von allen Ecken oder Seiten erfüllt wird oder eben nicht, und was dies für die Vielecke bedeutet. Beispielsweise werden Vielecke danach klassifiziert, ob die Winkel in allen Ecken kleiner beziehungsweise sind. In diesem Fall verlaufen dann alle Diagonalen im Innern des Vielecks. Andernfalls gibt es mindestens eine Diagonale außerhalb.
Die obigen Zeichnungen sind Beispiele von Vielecken, die verschiedene Eigenschaften zeigen. Im linken Vieleck sind alle (Innen-) Winkel kleiner als beziehungsweise . In dieser Situation spricht man auch von einem konvexen Vieleck. Anders ist es im mittleren Vieleck, in dem es eine Ecke mit einem größeren Winkel gibt. Im rechts dargestellten Vieleck sind alle Winkel gleich, woraus sich ein sehr gleichmäßiger Verlauf der Seiten ergibt.
Vielecke
5.4.8
Es seien Punkte in der Ebene gegeben, wobei eine natürliche Zahl mit sei. Hier werden Vielecke betrachtet, die dadurch entstehen, dass die Punkte nacheinander durch Strecken miteinander verbunden werden, sodass ein geschlossener Weg ohne Kreuzungspunkte entsteht und jeder der gegebenen Punkte zu genau zwei Strecken gehört. Dabei sollen je drei Punkte, die durch aufeinander folgende Strecken verbunden sind, nicht auf einer gemeinsamen Geraden liegen.
Ein Vieleck wird auch als -Eck oder Polygon bezeichnet.
Es seien Punkte in der Ebene gegeben, wobei eine natürliche Zahl mit sei. Hier werden Vielecke betrachtet, die dadurch entstehen, dass die Punkte nacheinander durch Strecken miteinander verbunden werden, sodass ein geschlossener Weg ohne Kreuzungspunkte entsteht und jeder der gegebenen Punkte zu genau zwei Strecken gehört. Dabei sollen je drei Punkte, die durch aufeinander folgende Strecken verbunden sind, nicht auf einer gemeinsamen Geraden liegen.
Ein Vieleck wird auch als -Eck oder Polygon bezeichnet.
- Die Punkte, die verbunden werden, heißen
Ecken des Vielecks, und
die Verbindungsstrecken heißen
Seiten des Vielecks.
- Jedes Vieleck kann man in einander nicht überlappende
Dreiecke zerlegen. Die Summe aller (Innen-)Winkel eines Vielecks beträgt
daher beziehungsweise .
- Die Verbindungsstrecken zwischen je zwei Ecken, die nicht auf derselben
Seite des Vielecks liegen, heißen die Diagonalen
des Vielecks.
Weitere Aussagen ergeben sich für Vielecke mit gleich langen Seiten und gleich großen Innenwinkeln. Für sind dies die gleichseitigen Dreiecke, und von den Vierecken sind es die Quadrate.
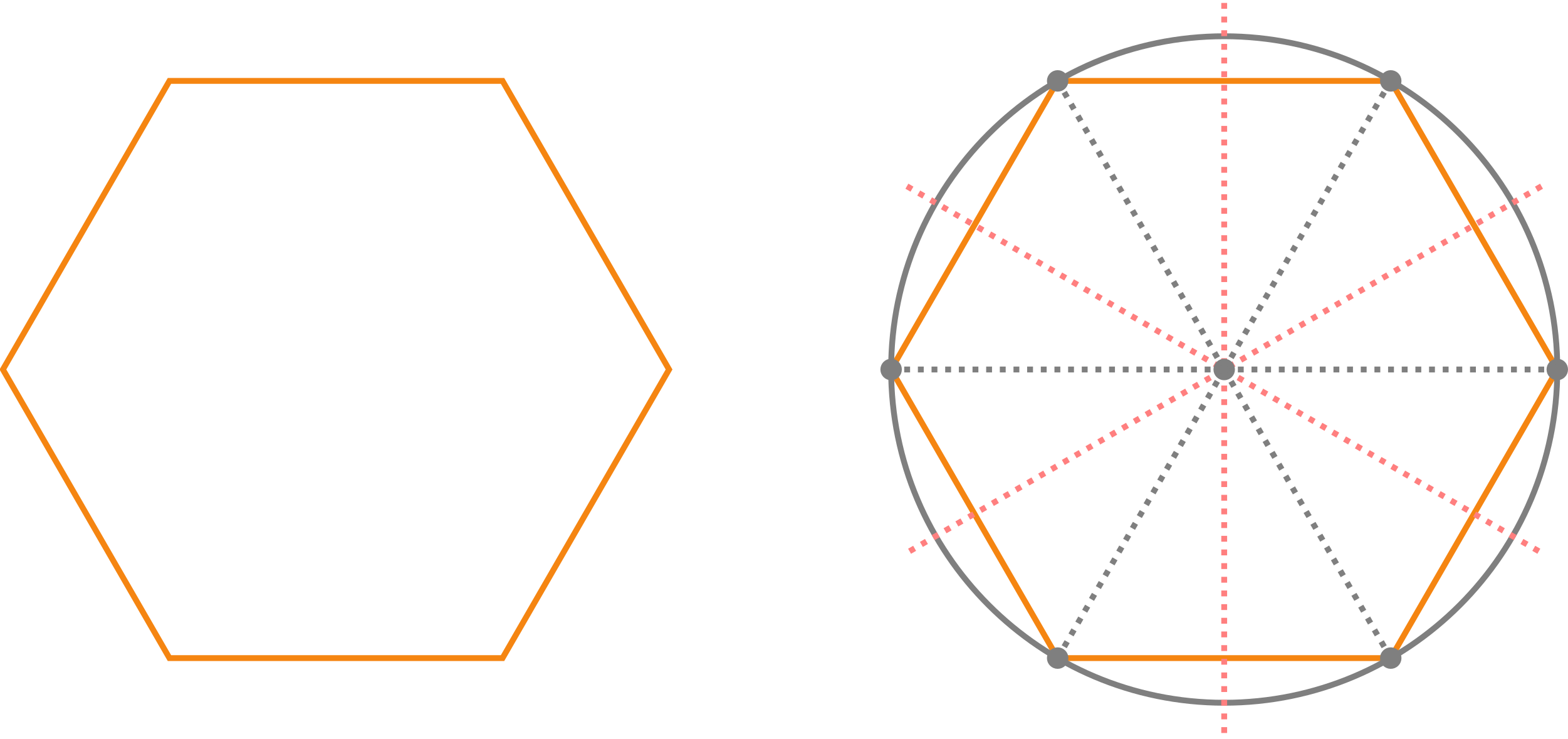
Abbildung 5.4.8: Skizze (C)
Regelmäßige Vielecke haben verschiedene Symmetrieeigenschaften. Alle Geraden durch die Seitenmitten, die senkrecht auf einer Seite stehen, schneiden sich in einem Punkt . Eine Spiegelung an einer solchen Geraden bildet das Vieleck auf sich ab.
Außerdem sind regelmäßige Vielecke in der Weise rotationssymmetrisch, dass das Vieleck auf sich abgebildet wird, wenn man es um um den Winkel dreht.
Die Ecken eines regelmäßigen Vielecks haben von alle denselben Abstand und liegen somit auf einem Kreis um .


