2. Geometrie
  3. Winkelfunktionen: Sinus und Co.
  4. Dreieck

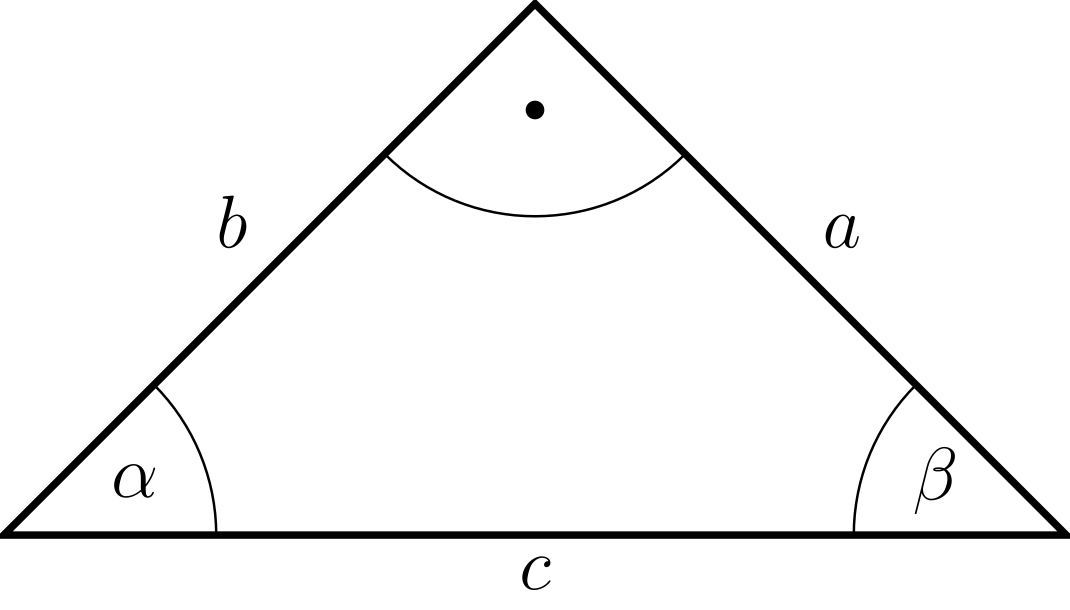
5.6.2 Trigonometrie am Dreieck



Fährt man eine Straße mit einem Gefälle von fünf Prozent bergab, nimmt die Höhe alle hundert Meter um fünf Meter ab. Dabei wird der Höhenunterschied im Vergleich zur Horizontalen betrachtet.

./_3034DA78_4x.png
Abbildung 5.6.1: Skizze  (C)



Demnach beträgt das Gefälle 100%, wenn der Höhenunterschied 100 m zwischen zwei Positionen beträgt, deren horizontaler Abstand 100 m beträgt. Geometrisch formuliert, ist die Verbindungsstrecke zwischen den beiden Punkte eine Diagonale eines Quadrats. Damit hat der Winkel zwischen der horizontalen Vergleichsstrecke und der Diagonalen, auf der man sich bewegt, das Winkelmaß von 45 ∘ .

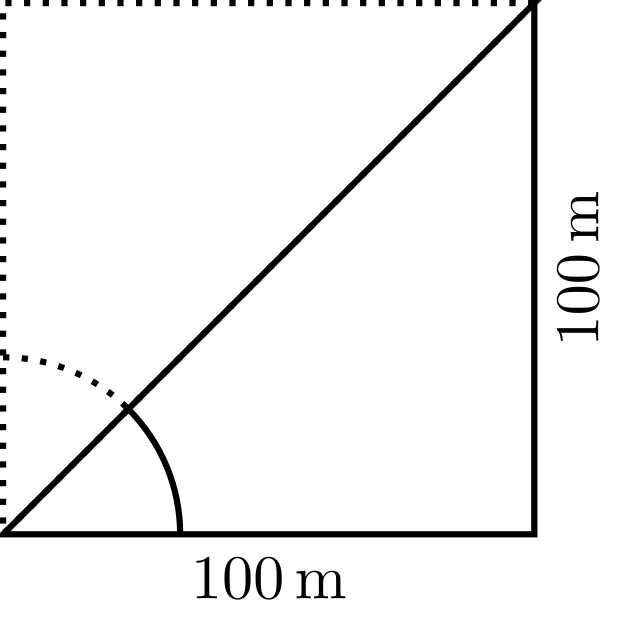
./_27954131_4x.png
Abbildung 5.6.2: Skizze  (C)



Dies kann man auch so formulieren: Einem Winkel von 45 ∘ entspricht eine Steigung von 100 m 100 m =1, das heißt ein Streckenverhältnis von 1 von vertikaler zu horizontaler Strecke. Aufgrund der Strahlensätze ist das Streckenverhältnis von den Längen der einzelnen Strecken unabhängig. Es hängt nur davon ab, wie die Strahlen zueinander verlaufen, also wie groß der Winkel zwischen ihnen ist. Wenn diese Zuordnung zwischen Winkel und Streckenverhältnis auch für andere Winkel bekannt ist, kann man damit viele konstruktive Aufgabenstellungen lösen. Beispielsweise kann die Höhe zu einem gegebenen Winkel bestimmt werden.

Schon die Frage, welches Verhältnis zu einem Winkel von 30 ∘ gehört, zeigt allerdings, dass die Bestimmung der Zuordung zwischen Winkel und Streckenverhältnis im Allgemeinen jedoch nicht so einfach ist. Deshalb wurden die aufwändig bestimmten Werte anfangs in großen Tafelwerken aufgeschrieben, um dann einfach nachgeschlagen werden zu können. Inzwischen sind die Werte mittels Taschenrechner und Computer praktisch überall verfügbar. Die gebräuchlichsten Zuordnungen von Winkel zu einem Streckenverhältnis werden im Folgenden vorgestellt. Sie werden Winkelfunktionen oder trigonometrische Funktionen genannt, und das mathematische Gebiet, das sich mit ihren Eigenschaften befasst, heißt Trigonometrie.

Die trigonometrischen Funktionen im rechtwinkligen Dreieck 5.6.1  
Es werden die gebräuchlichsten Winkelfunktionen als Zuordnungen zwischen Winkel und Seitenverhältnissen in einem rechtwinkligen Dreieck beschrieben. Die Winkelfunktionen heißen auch trigonometrische Funktionen. Dabei bezeichnet x einen Winkel in einem rechtwinkligen Dreieck, der kein rechter Winkel ist. Die Gegenkathete ist die Seite, die dem Winkel x gegenüberliegt, und die andere Kathete wird Ankathete genannt.

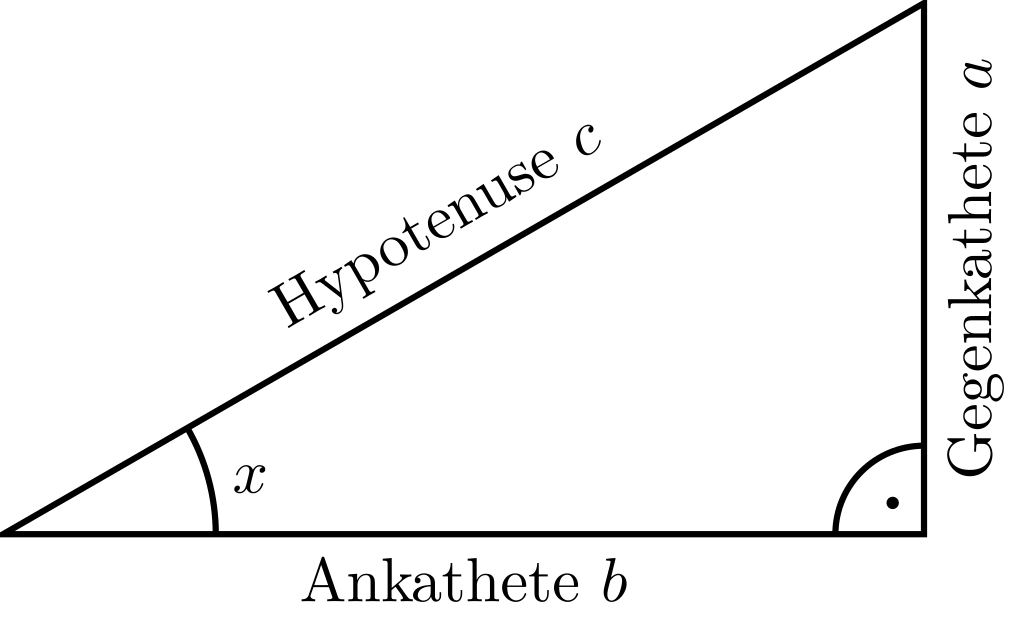
./_01494702_4x.png
Abbildung 5.6.3: Skizze  (C)



  • Die Zuordnung zwischen Winkel x und dem Verhältnis zwischen Gegenkathete a und Ankathete b wird als Tangens

    tan(x):= Gegenkathete Ankathete = a b

    bezeichnet.

  • Die Zuordnung zwischen Winkel x und dem Verhältnis zwischen Ankathete b und Hypotenuse c wird als Kosinus

    cos(x):= Ankathete Hypotenuse = b c

    bezeichnet.

  • Die Zuordnung zwischen Winkel x und dem Verhältnis zwischen Gegenkathete a und Hypotenuse c wird als Sinus

    sin(x):= Gegenkathete Hypotenuse = a c

    bezeichnet.



Demnach beschreibt der Tangens die Zuordnung zwischen dem Neigungswinkel und dem Verhältnis zwischen Höhe und Breite, also der Steigung. Dies ist auch im Kapitel 8 im Kontext der geometrischen Interpretation der Ableitung von Bedeutung.

Der Tangens des Winkels α ist nach der Definition

tan(α)= a b = a b · c c = a c · c b = sin(α) cos(α)  .

Somit genügt es, die Werte von Sinus und Kosinus zu kennen, um auch den Tangens berechnen zu können.

Beispiel 5.6.2  
Von einem Dreieck ist bekannt, dass es einen rechten Winkel γ= π 2 =90 ∘ hat. Die Seite c ist 5 cm, die Seite a ist 2,5 cm lang. Es sollen jeweils der Sinus, Kosinus und Tangens des Winkels α bestimmt werden:

Der Sinus lässt sich sofort aus den Angaben berechnen:

sin(α)= a c = 2,5 cm 5 cm =0,5 .

Für den Kosinus wird die Länge der Seite b benötigt, welche man mithilfe des Satzes von Pythagoras erhält:

b2 = c2 - a2  .

Daraus folgt:

cos(α)= b c = c2 - a2 c = (5 cm)2 - (2,5 cm)2 5 cm =0,866 .

Damit ergibt sich für den Tangens

tan(α)= sin(α) cos(α) = 0,5 0,866 =0,5773 .



Aufgabe 5.6.3  
Es sollen einige Werte der Winkelfunktionen Sinus, Kosinus und Tangens näherungsweise grafisch bestimmt werden. Gehen Sie von rechtwinkligen Dreiecken mit einer Hypotenuse c=5 aus. Zeichnen Sie mithilfe des Thaleskreises rechtwinklige Dreiecke für die Winkel

α∈{10 ∘ ;20 ∘ ;30 ∘ ;40 ∘ ;45 ∘ ;50 ∘ ;60 ∘ ;70 ∘ ;80 ∘ } .

Fertigen Sie Ihre Zeichnungen im Maßstab 1 Längeneinheit = ^ 2 cm an, und schreiben Sie die Messwerte zu den Seiten a und b in eine Tabelle.

Berechnen Sie zu jedem Winkel mit den gemessenen Werten den Sinus, Kosinus und Tangens, und überlegen Sie sich anschließend, wo auch Werte zu α=0 ∘ und zu α=90 ∘ existieren. Tragen Sie anschließend die Werte von Sinus und Kosinus in Abhängigkeit des Winkels α in ein Diagramm ein.



Wenn man sich die Ergebnisse aus der letzten Aufgabe nochmals genauer ansieht, kann man auf verschiedene Ideen kommen, sie zu interpretieren, und dann einige Zusammenhänge erkennen.

  • Mit zunehmendem Winkel α nimmt die Gegenkathete a zu und die Ankathete b ab.

    Ebenso verhalten sich sin(α)~a und cos(α)~b.

  • Mit zunehmendem Winkel α nimmt a in dem gleichen Maß zu wie b mit dem von 90 ∘ aus fallenden Winkel α abnimmt. Im Thaleskreis sind die beiden Dreiecke mit den entgegengesetzten Werten für a und b die zwei Lösungen für die Konstruktion eines rechtwinkligen Dreiecks mit gegebener Hypotenuse und gegebener Höhe (siehe auch das Beispiel 5.3.7).

  • Für den Winkel β=90 ∘ -α ist die Ankathete die Seite im rechtwinkligen Dreieck, die aus Sicht des Winkels α als Gegenkathete bezeichnet wird (und umgekehrt). Somit gilt

    sin(α)=cos(90 ∘ -α)=cos( π 2 -α)

    und

    cos(α)=sin(90 ∘ -α)=sin( π 2 -α) .



  • Bei α=45 ∘ sind die Katheten und damit auch Sinus und Kosinus von α gleich. Diese Beobachtung führte eingangs umgekehrt zur Bestimmung des Steigungswinkels.

  • Der Tangens, also das Verhältnis von a zu b, steigt mit zunehmendem Winkel α von Null ins „Unendliche“.



Im folgenden Beispiel wird die Überlegung aus der Einleitung fortgesetzt, die auf ein Dreieck mit einem Winkel von 45 ∘ führte, um den zugehörigen Sinuswert exakt zu berechnen.

Beispiel 5.6.4  
Es soll der Sinus des Winkels α=45 ∘ nun exakt berechnet, also nicht wie in Aufgabe 5.6.3 aus gemessenen (und damit fehlerbehafteten) Werten bestimmt werden.

Wenn im rechtwinkligen Dreieck mit γ=90 ∘ der Winkel α gleich 45 ∘ ist, so muss wegen der Summe der Winkel α+β+γ=π=180 ∘ der Winkel β auch gleich 45 ∘ =π/4 sein. Folglich sind die beiden Katheten a und b gleich lang. Ein Dreieck mit zwei gleich langen Seiten nennt man gleichschenklig.

./_A82BFDA7_4x.png
Abbildung 5.6.5: Skizze  (C)

Es gilt:

sin(α)=sin(45 ∘ )= a c  .

Außerdem gilt

a2 + b2 =2 a2 = c2    ⇒   c=2·a ,

woraus

sin(45 ∘ )=sin(π/4)= a 2·a = 1 2 ·2

folgt. In der Aufgabe 5.6.3 wurde der Sinus von 45 ∘ durch einen Wert von 0,7 angenähert, was dem tatsächlichen Wert von 1 2 ·2 schon recht nahe kommt.


Im nächsten Beispiel wird der Sinuswert zum Winkel α=60 ∘ berechnet. Hierfür wird zunächst nicht ein rechtwinkliges Dreieck sondern ein Dreieck mit drei gleich langen Seiten betrachtet. Mit einer geschickten Zerlegung und Berechnung einer weiteren „Hilfsgröße“ erhält man daraus das gesuchte Ergebnis.

Beispiel 5.6.5  
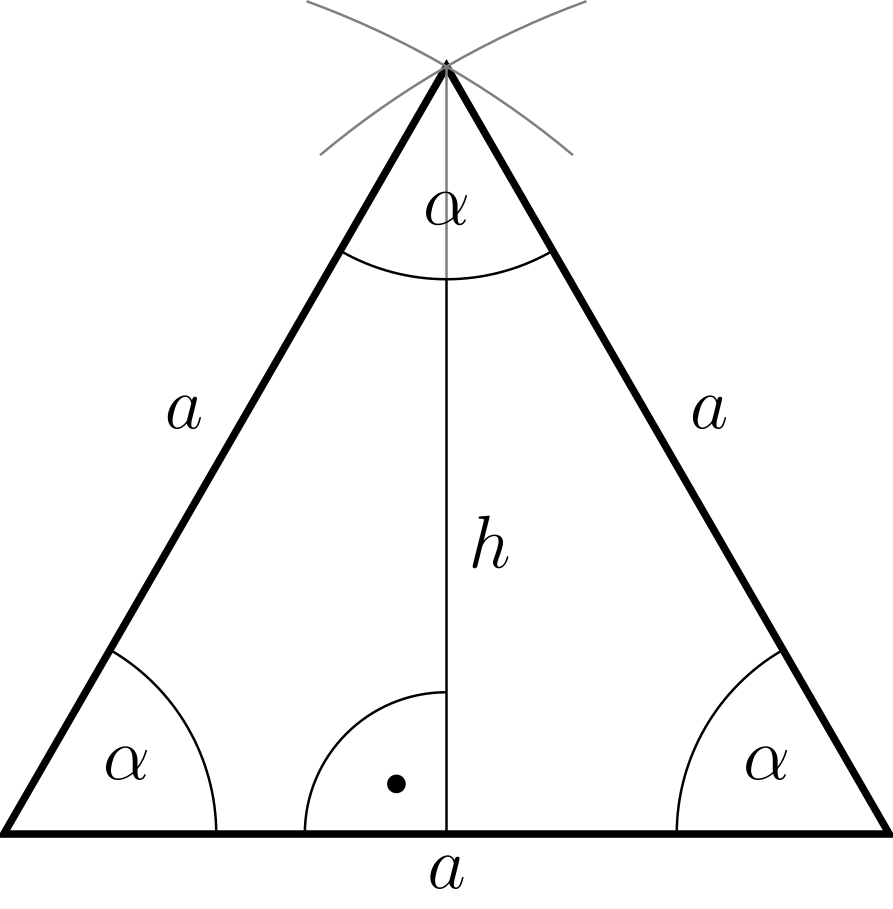
In diesem Beispiel soll ein gleichseitiges Dreieck betrachtet werden, um sin(60 ∘ ) zu berechnen. Wie der Name sagt, sind in diesem Dreieck alle Seiten gleich lang, und auch die Winkel sind alle gleich groß, nämlich α=β=γ= 180 ∘ 3 =60 ∘ = π 3 . Das Dreieck ist nach dem Kongruenzsatz „sss“ mit der Angabe einer Seite a eindeutig bestimmt, und man erhält dieses, indem man die Seite a zeichnet und mit dem Zirkel einen Kreis vom Radius a um jede Ecke schlägt. Der Schnittpunkt der Kreise ist nun die dritte Ecke.

Dieses Dreieck hat keinen rechten Winkel. Zeichnet man eine Höhe h auf eine der Seiten a ein, so erhält man zwei kongruente Dreiecke mit je einem rechten Winkel.

Es gilt nun:

sin(α)=sin(60 ∘ )= h a  .

Nach dem Satz von Pythagoras ist

( a 2 )2 + h2 = a2  .

Daraus folgt

h2 = 3 4 a2     und somit    h= 1 2 3·a .

./_F6C020D2_4x.png
Abbildung 5.6.6: Skizze  (C)

Damit erhält man den gesuchten Wert

sin(60 ∘ )=sin( π 3 )= h a = 1 2 ·3 .

Aus diesem Dreieck kann man noch den Sinus eines weiteren Winkels berechnen: Die Höhe h teilt den oberen Winkel in zwei gleiche Teile, sodass man in den beiden kleinen kongruenten Dreiecken jeweils den Winkel 30 ∘ = π 6 erhält. Es ist nun

sin(30 ∘ )=sin( π 6 )= a/2 a = 1 2  .



Aufgabe 5.6.6  
Berechnen Sie den exakten Wert des Kosinus für die Winkel α1 =30 ∘ , α2 =45 ∘ und α3 =60 ∘ . Verwenden Sie dazu die Ergebnisse aus dem vorherigen Beispiel und aus der Aufgabe 5.6.3.



In einer kleinen Tabelle werden die gefundenen Werte für oft verwendete Winkel zusammengestellt: Hier wird in der mit x bezeichneten ersten Zeile der Winkel im Bogenmaß und in der mit α bezeichneten letzten Zeile der Winkel im Gradmaß notiert.

\ifttm\special{html:}\fi\[ \begin{array}[t]{l|*{5}{c}} x & 0 & \tfrac{\pi}{6} & \tfrac{\pi}{4} & \tfrac{\pi}{3} & \tfrac{\pi}{2} \\[1mm] \hline \sin & 0 = \frac{1}{2} \cdot \sqrt{0} & \frac{1}{2} = \frac{1}{2} \cdot \sqrt{1} & \frac{1}{2} \cdot \sqrt{2} & \frac{1}{2} \cdot \sqrt{3} & \frac{1}{2} \cdot \sqrt{4} = 1 \\[1mm] \cos & 1 = \frac{1}{2} \cdot \sqrt{4} & \frac{1}{2} \cdot \sqrt{3} & \frac{1}{2} \cdot \sqrt{2} & \frac{1}{2} \cdot \sqrt{1} = \frac{1}{2} & \frac{1}{2} \cdot \sqrt{0} = 0 \\[1mm] \tan & 0 & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} & - \\[1mm] \hline \alpha & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} %% \end{array} \]

Diese Werte sollte man sich merken. Die Werte der trigonometrischen Funktionen für andere Winkel sind in Tabellen abgelegt bzw. mit dem Taschenrechner berechenbar.

Damit kann man dann aus einem Winkel und einem Abstand ganz einfach eine Höhe berechnen. Ist nämlich s der Abstand zu einem Gebäude mit Flachdach, das unter einem Winkel x beobachtet wird, ergibt sich aus tan(x)= h s nämlich h=s·tan(x). Ebenso können auch cos und sin verwendet werden, um Längen zu berechnen. Dieser Zusammenhang zwischen Winkeln und Längen wird oft verwendet.

Beispielsweise kann man so einen Flächeninhalt berechnen, auch wenn eine benötigte Länge nicht unmittelbar gegeben ist. Im folgenden Beispiel ist es eine Höhe h in einem Dreieck, die zu berechnen ist. Da h, ausgehend von einer Ecke, hier C genannt, senkrecht auf der Geraden der gegenüberliegenden Seite c= AB ‾ steht, bilden die Ecken von h und A bzw. B ein rechtwinkliges Dreieck. Mit einer Angabe zu einem Winkel und der entsprechenden Seite kann dann die Höhe aus sin(α)= h b oder aus sin(β)= h a berechnet werden, wobei von den konventionellen Bezeichnungen ausgegangen wurde.

Aufgabe 5.6.7  
Berechnen Sie den Flächeninhalt F eines Dreiecks mit den Seiten c=7 und b=3 sowie dem Winkel α=30 ∘ zwischen den Seiten c und b.

Ergebnis: F  =