10.2.2 Geraden in der Ebene und im Raum
In Kapitel 9 wurden Geraden in der Ebene mittels Koordinatengleichungen für die Punkte auf den Geraden bezüglich eines festen Koordinatensystems beschrieben. Zum Beispiel ist in dieser Beschreibung eine Gerade mit Steigung und Achsenabschnitt gegeben als Punktmenge
wofür man oft kurz auch nur die Koordinatengleichung (hier in Normalform) angibt:
Das folgende Bild zeigt die Gerade:
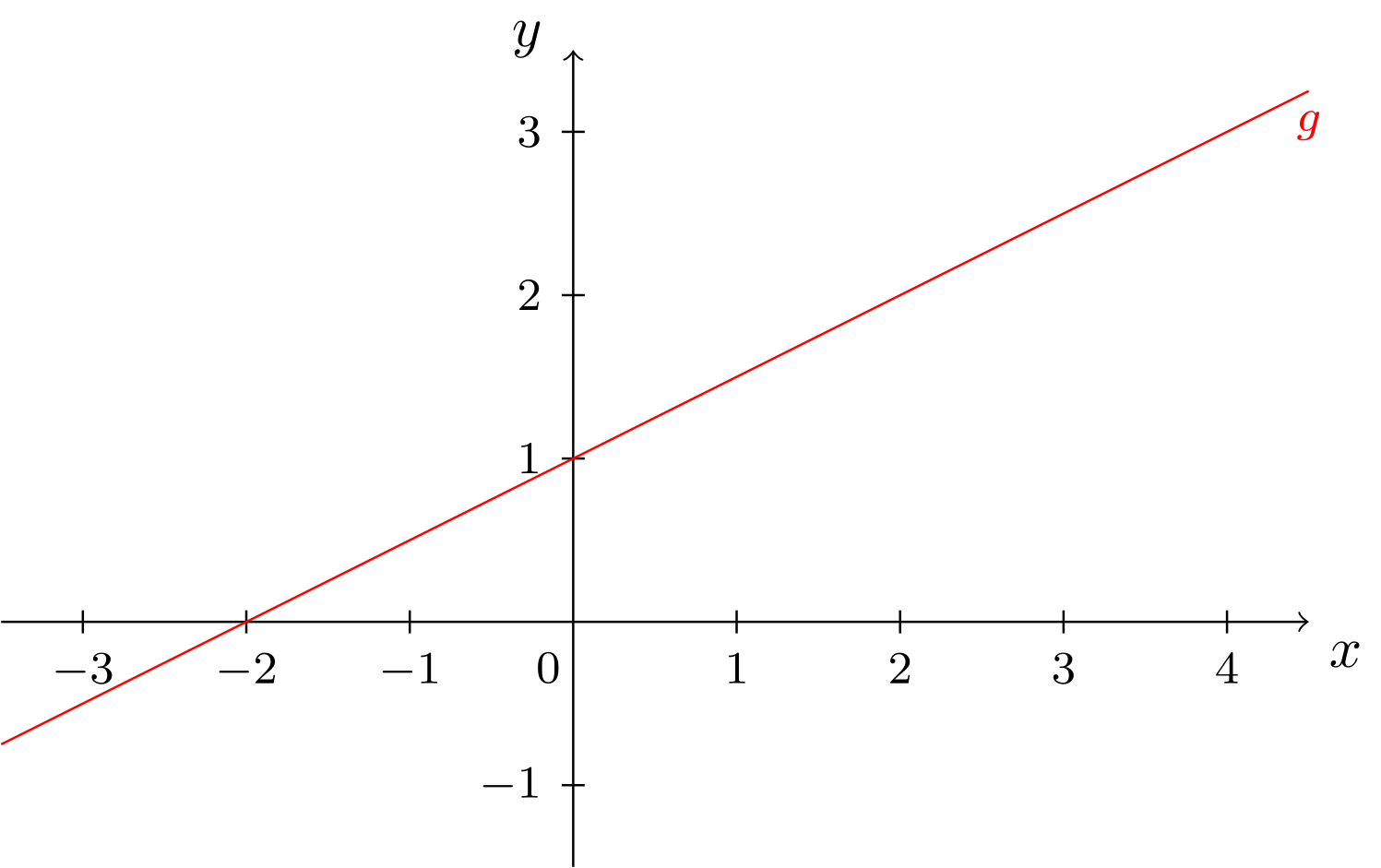
Im Folgenden sollen die Punkte auf der Geraden nun durch ihre zugehörigen Ortsvektoren beschrieben werden. Die nachstehende Überlegung führt auf diese Beschreibung: Die Punkte auf der obigen Geraden erfüllen die Gleichung
für ihre Koordinaten. Man kann diese Gleichung für die -Koordinaten in die Punkte einsetzen und erhält, dass die Gerade durch Punkte der Form mit gebildet wird. Die zu diesen Punkten gehörenden Ortsvektoren sollen mit bezeichnet sein. Dann gilt
mit . Das heißt die Gerade kann unter Benutzung von Ortsvektoren auch beschrieben werden mittels
Mit anderen Worten, die Punkte auf werden gebildet durch die Summe des Vektors und allen möglichen Vielfachen des Vektors , also allen zu kollinearen Vektoren. Das folgende Bild stellt diese Sichtweise auf Geraden dar:
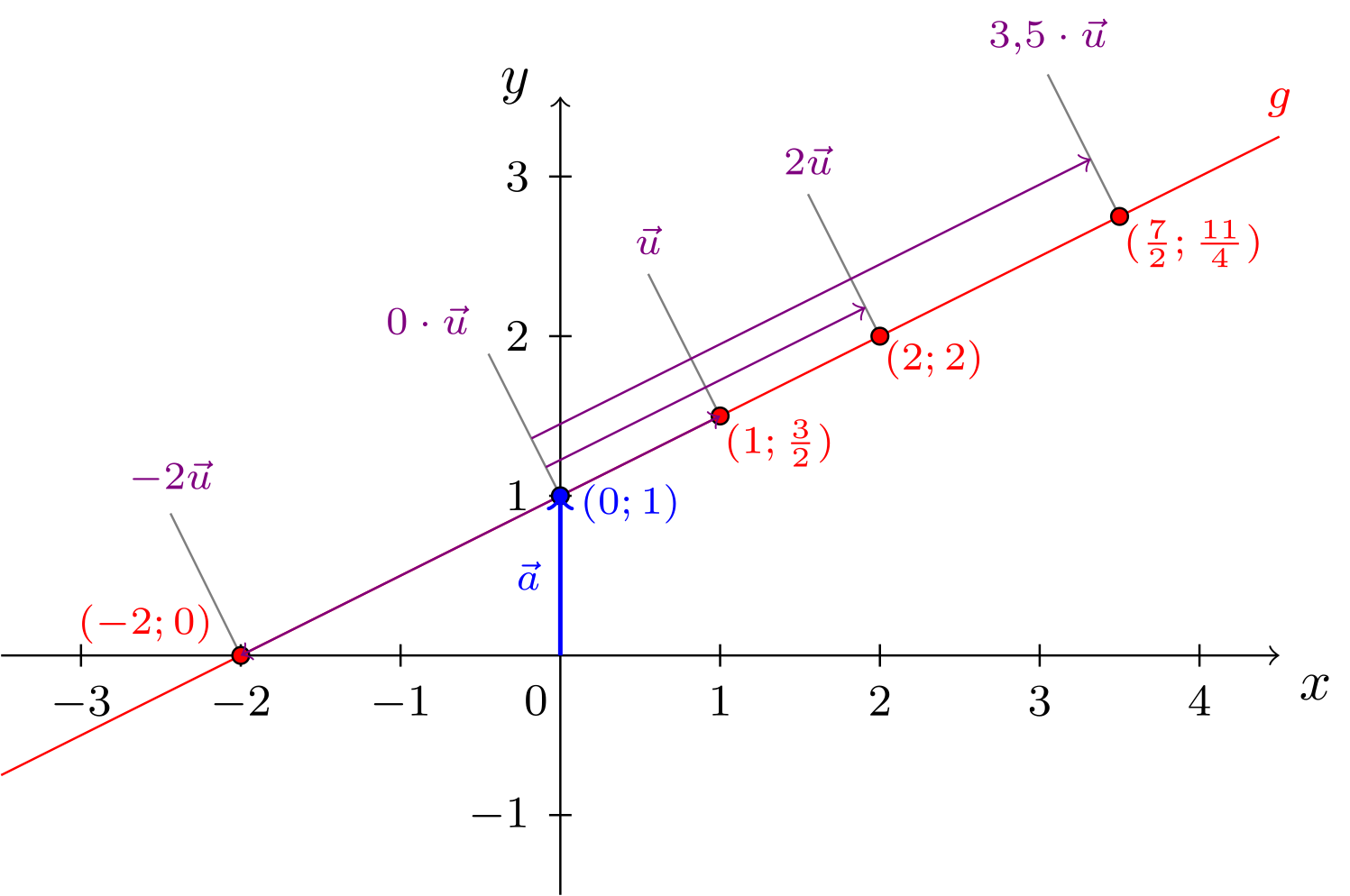
Die nächste Infobox stellt die wichtigsten Begriffe, Methoden und Konzepte zu dieser als Punkt-Richtungsform oder Parameterform bezeichneten Darstellungsweise von Geraden zusammen.
Man stellt hier sofort fest, dass die Parameterform einer Geraden nicht eindeutig ist. Als Aufpunkt kann jeder Punkt auf der Geraden dienen, und auch als Richtungsvektor hat man beliebig viele kollineare Vektoren zur Auswahl. So wird zum Beispiel die Gerade mit der Koordinatengleichung
aus dem einführenden Beispiel nicht nur durch
in Parameterform dargestellt, sondern auch durch
oder
Oft benutzt man Darstellungen mit einem möglichst einfachen Richtungsvektor. Es sollte nur darauf geachtet werden, dass bei Darstellungen der gleichen Geraden mittels unterschiedlicher Richtungs- oder Aufpunktvektoren jeweils andere Variablen für den Parameter verwendet werden, da gleiche Parameterwerte in unterschiedlichen Darstellungen zu unterschiedlichen Punkten auf der Geraden führen. So ergibt beispielsweise der Parameterwert in der entsprechenden obigen Parameterform für den Punkt
auf , der Parameterwert der entsprechenden obigen Parameterform für den Punkt
auf .
Das folgende Beispiel zeigt einige Anwendungen der Punkt-Richtungsform.
wofür man oft kurz auch nur die Koordinatengleichung (hier in Normalform) angibt:
Das folgende Bild zeigt die Gerade:

Abbildung 10.2.3: Skizze (C)
Im Folgenden sollen die Punkte auf der Geraden nun durch ihre zugehörigen Ortsvektoren beschrieben werden. Die nachstehende Überlegung führt auf diese Beschreibung: Die Punkte auf der obigen Geraden erfüllen die Gleichung
für ihre Koordinaten. Man kann diese Gleichung für die -Koordinaten in die Punkte einsetzen und erhält, dass die Gerade durch Punkte der Form mit gebildet wird. Die zu diesen Punkten gehörenden Ortsvektoren sollen mit bezeichnet sein. Dann gilt
mit . Das heißt die Gerade kann unter Benutzung von Ortsvektoren auch beschrieben werden mittels
Mit anderen Worten, die Punkte auf werden gebildet durch die Summe des Vektors und allen möglichen Vielfachen des Vektors , also allen zu kollinearen Vektoren. Das folgende Bild stellt diese Sichtweise auf Geraden dar:

Abbildung 10.2.4: Skizze (C)
Die nächste Infobox stellt die wichtigsten Begriffe, Methoden und Konzepte zu dieser als Punkt-Richtungsform oder Parameterform bezeichneten Darstellungsweise von Geraden zusammen.
Info
10.2.2
- Eine Gerade in der Ebene ist in Punkt-Richtungsform oder Parameterform gegeben als Menge von Ortsvektoren
oft kurz geschrieben als
Hierbei wird als Parameter, als Aufpunktvektor und als Richtungsvektor der Geraden bezeichnet. Die Ortsvektoren zeigen dann zu den einzelnen Punkten auf der Geraden. Der Aufpunktvektor ist der Ortsvektor eines festen Punktes auf der Geraden, der als Aufpunkt bezeichnet wird. Die Vielfachen von sind alle Vektoren, die kollinear zu sind:
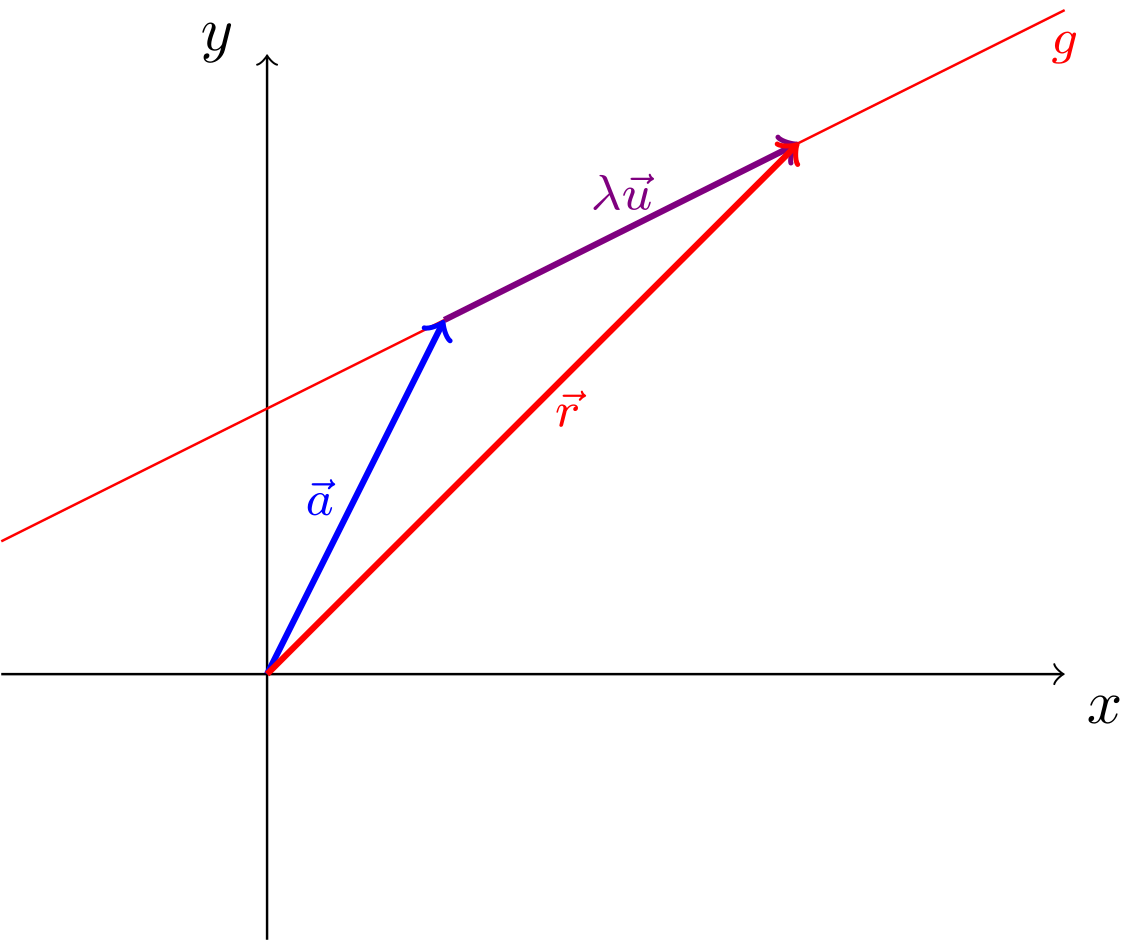 Abbildung 10.2.5: Skizze (C)
Abbildung 10.2.5: Skizze (C)
- Für eine Gerade , die durch Angabe einer Geradengleichung in Normalform
vorliegt, kann eine Punkt-Richtungsform angegeben werden, indem die Ortsvektoren gebildet werden. Die Punkt-Richtungsform lautet dann
mit dem Richtungsvektor und dem Aufpunktvektor .
- Für eine Gerade , die in Parameterform
vorliegt, kann eine zugehörige Geradengleichung folgendermaßen ermittelt werden: Der Richtungsvektor liefert durch Anlegen eines Steigungsdreiecks sofort die Steigung der Geraden. Es gilt
(Hierfür muss sein. Der Spezialfall wird im Beispiel unten behandelt.) Nach den Methoden aus Abschnitt 9.2.2 benötigt man zur Angabe der Geradengleichung in Normalform nun nur noch einen Punkt auf der Geraden, aus dem man den Achsenabschnitt bestimmt. Hierfür benutzt man am einfachsten den Aufpunktvektor .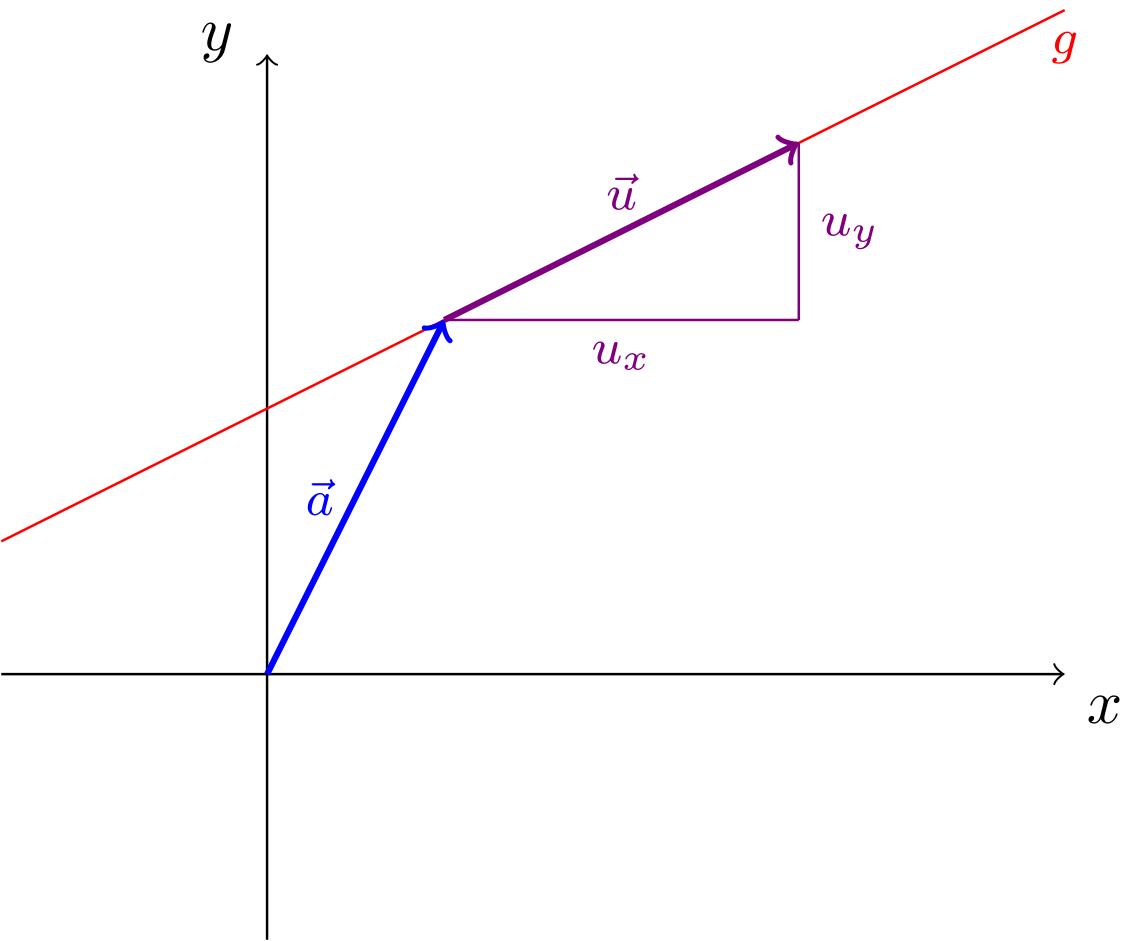 Abbildung 10.2.6: Skizze (C)
Abbildung 10.2.6: Skizze (C)
Man stellt hier sofort fest, dass die Parameterform einer Geraden nicht eindeutig ist. Als Aufpunkt kann jeder Punkt auf der Geraden dienen, und auch als Richtungsvektor hat man beliebig viele kollineare Vektoren zur Auswahl. So wird zum Beispiel die Gerade mit der Koordinatengleichung
aus dem einführenden Beispiel nicht nur durch
in Parameterform dargestellt, sondern auch durch
oder
Oft benutzt man Darstellungen mit einem möglichst einfachen Richtungsvektor. Es sollte nur darauf geachtet werden, dass bei Darstellungen der gleichen Geraden mittels unterschiedlicher Richtungs- oder Aufpunktvektoren jeweils andere Variablen für den Parameter verwendet werden, da gleiche Parameterwerte in unterschiedlichen Darstellungen zu unterschiedlichen Punkten auf der Geraden führen. So ergibt beispielsweise der Parameterwert in der entsprechenden obigen Parameterform für den Punkt
auf , der Parameterwert der entsprechenden obigen Parameterform für den Punkt
auf .
Das folgende Beispiel zeigt einige Anwendungen der Punkt-Richtungsform.
Beispiel
10.2.3
- Für die Gerade in der Ebene, welche durch die Geradengleichung
gegeben ist, sollen zwei verschiedene Parameterformen ermittelt werden.
Zunächst wird die Geradengleichung auf Normalform gebracht:
Punkte auf haben also die Form mit , welche durch Ortsvektoren mit beschrieben werden. Folglich ist eine mögliche Parameterform durch
gegeben. Für eine andere Parameterform können ein beliebiger anderer Richtungsvektor, der kollinear zu ist, und ein beliebiger anderer Aufpunkt auf gewählt werden. Zum Beispiel ist kollinear zu , da gilt. Und ist ein anderer passender Aufpunktvektor, da der Punkt offenbar die Geradengleichung erfüllt. Folglich ist
eine weitere mögliche Parameterform der Geraden .
- Auch für eine Gerade, deren Koordinatengleichung nicht auf Normalform gebracht werden kann, wie etwa
kann eine Punkt-Richtungsform angegeben werden.
Punkte auf der Geraden haben alle die Form für mit zugehörigen Ortsvektoren für . Da gilt, ist eine mögliche Punkt-Richtungsform für durch
gegeben.
- Für die Gerade in Parameterform mit
soll die zugehörige Geradengleichung in Normalform ermittelt werden.
Der Richtungsvektor liefert die Steigung . Somit hat die Geradengleichung in Normalform die Form
Der Aufpunktvektor von lautet . Somit kann zur Bestimmung des Achsenabschnitts der Aufpunkt eingesetzt werden:
Somit ergibt sich
- Auch für eine Gerade in Parameterform wie etwa
für welche die -Komponente des Richtungsvektors ist, kann eine zugehörige Geradengleichung ermittelt werden.
Der Richtungsvektor mit -Komponente gleich impliziert, dass die Gerade parallel zur -Achse verläuft. Folglich hat die Geradengleichung die Form
Die Konstante kann wieder durch Einsetzen des Aufpunkts bestimmt werden. Man erhält , und folglich gilt
- Zu den beiden Punkten und ist die Gerade in Parameterform zu bestimmen.
Als Richtungsvektor dient hier der Verbindungsvektor
und als Aufpunktvektor der Ortsvektor von einem der gegebenen Punkte, zum Beispiel
Somit gilt
Bild hierzu: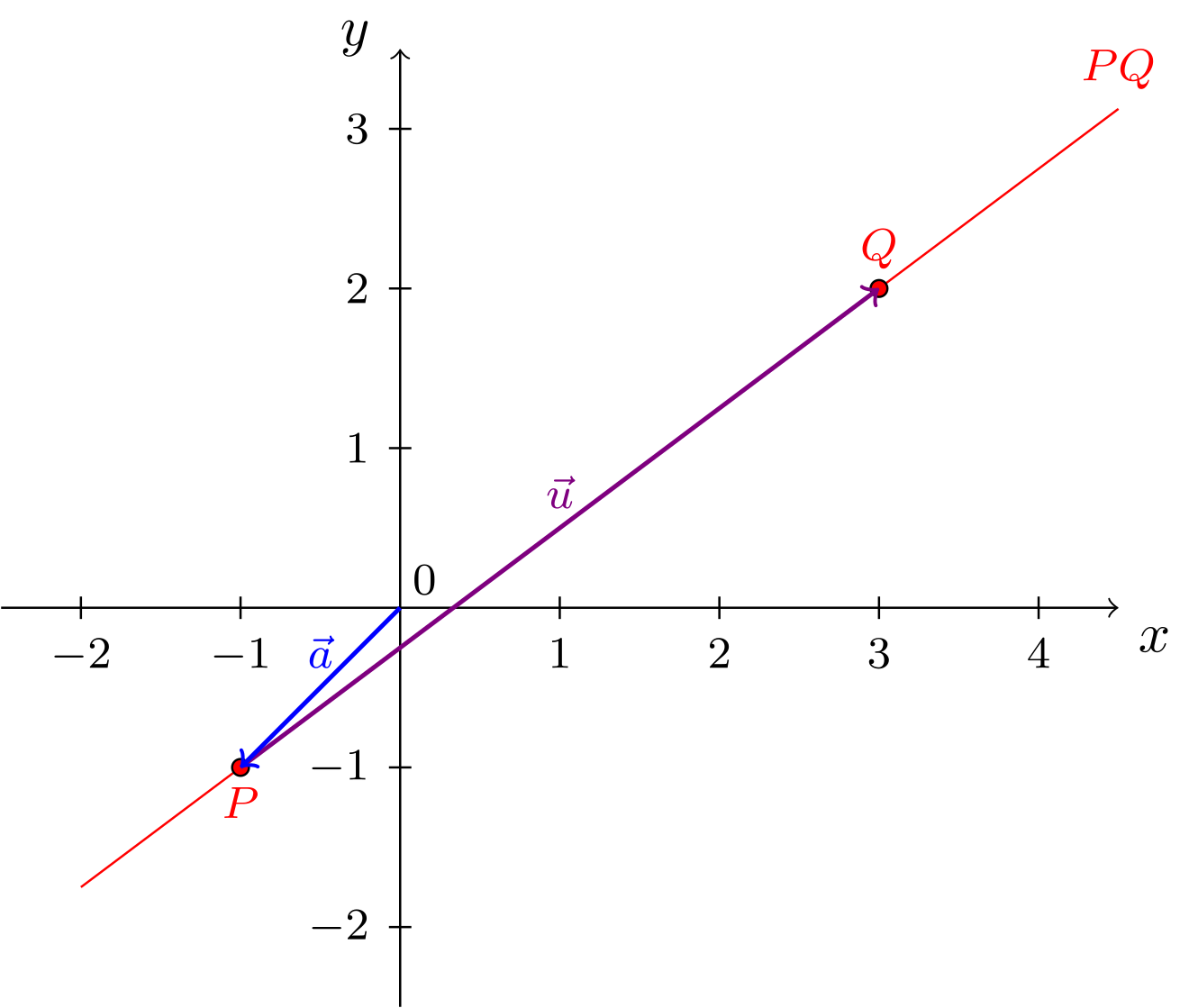 Abbildung 10.2.7: Skizze (C)
Abbildung 10.2.7: Skizze (C)
Aufgabe 10.2.4
- Gegeben ist die Gerade mittels
in Parameterform. Bestimmen Sie die Koordinatengleichung von in Normalform:
 .
.
-
Die Gerade mit der Koordinatengleichung
hat die Parameterform
Bestimmen Sie die fehlenden Werte und .


- Gegeben sind die beiden Punkte und . Welche der folgenden Parameterformen sind korrekte Darstellungen der Geraden ?
Richtig  Falsch
Falsch

(i) Richtig  Falsch
Falsch

(ii) Richtig  Falsch
Falsch

(iii) Richtig  Falsch
Falsch

(iv) Richtig  Falsch
Falsch

(v) Richtig  Falsch
Falsch

(vi)
-
Für welchen Wert von liegt der Punkt mit dem Ortsvektor
auf der Geraden
und für welchen Parameterwert gilt dann ?


Geraden im Raum lassen sich im Gegensatz zu Geraden in der Ebene nicht mit Hilfe einer Koordinatengleichung darstellen. Hier hilft aber die Punkt-Richtungsform, die sich problemlos vom zwei- auf den dreidimensionalen Fall überträgt:
Auch hier im dreidimensionalen Fall ist - analog zur Situation bei Geraden in der Ebene - die Parameterform einer Geraden nie eindeutig. Das folgende Beispiel zeigt die Anwendung von Geraden in Parameterform im Raum.
Beispiel
10.2.6
Zu den beiden gegebenen Punkten und sind zwei unterschiedliche Darstellungen der Geraden in Parameterform anzugeben.
Der Verbindungsvektor dient als Richtungsvektor:
Der Punkt kann als Aufpunkt benutzt werden. Damit ergibt sich die Parameterform
Weitere zulässige Richtungsvektoren müssen kollinear zu sein. Zum Beispiel:
Dann kann zum Beispiel auch der Punkt als Aufpunkt benutzt werden, und man erhält
als weitere korrekte Punkt-Richtungsform für die Gerade .
Zu den beiden gegebenen Punkten und sind zwei unterschiedliche Darstellungen der Geraden in Parameterform anzugeben.
Der Verbindungsvektor dient als Richtungsvektor:
Der Punkt kann als Aufpunkt benutzt werden. Damit ergibt sich die Parameterform
Weitere zulässige Richtungsvektoren müssen kollinear zu sein. Zum Beispiel:
Dann kann zum Beispiel auch der Punkt als Aufpunkt benutzt werden, und man erhält
als weitere korrekte Punkt-Richtungsform für die Gerade .
Aufgabe 10.2.7
- Die Gerade , welche durch die gegebenen Punkte und verläuft,
hat die Parameterform
Bestimmen Sie die fehlenden Werte , , und .




-
Für welchen Wert von liegt der Punkt mit dem Ortsvektor
auf der Geraden
und für welchen Parameterwert gilt dann ?




