9.2.2 Koordinatengleichungen für Geraden
Es wird nun zunächst die allgemeinste Form einer Koordinatengleichung für eine Gerade vorgestellt. Damit lässt sich jede Gerade in der Ebene als unendliche Punktmenge bezüglich eines gegebenen Koordinatensystems angeben.
Info
9.2.2
Eine Gerade im ist eine Punktmenge
Dabei sind reelle Zahlen, welche die Gerade festlegen. Die Zahlen und dürfen dabei nicht beide gleich sein. Die lineare Gleichung
heißt Geradengleichung oder genauer, um sie von anderen möglichen Formen von Geradengleichungen zu unterscheiden, auch Koordinatenform der Geradengleichung. Um die oben stehende Mengenschreibweise für Geraden abzukürzen, hat es sich auch eingebürgert, nur die Variable für die Gerade und die Geradengleichung anzugeben:
Eine Gerade im ist eine Punktmenge
Dabei sind reelle Zahlen, welche die Gerade festlegen. Die Zahlen und dürfen dabei nicht beide gleich sein. Die lineare Gleichung
heißt Geradengleichung oder genauer, um sie von anderen möglichen Formen von Geradengleichungen zu unterscheiden, auch Koordinatenform der Geradengleichung. Um die oben stehende Mengenschreibweise für Geraden abzukürzen, hat es sich auch eingebürgert, nur die Variable für die Gerade und die Geradengleichung anzugeben:
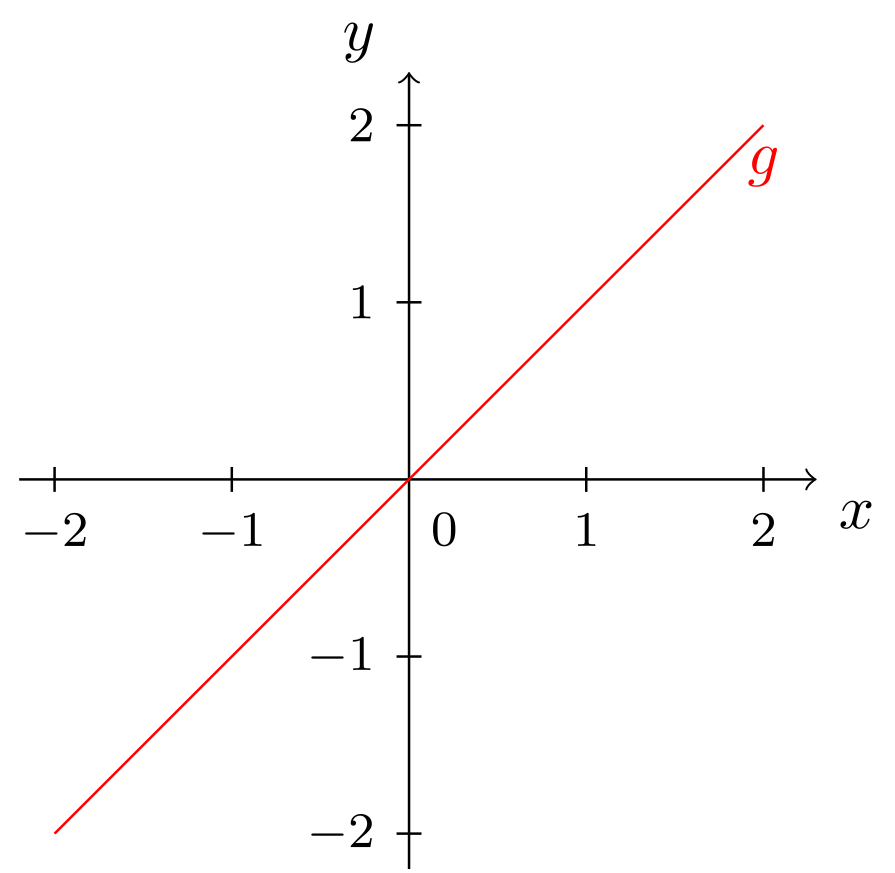
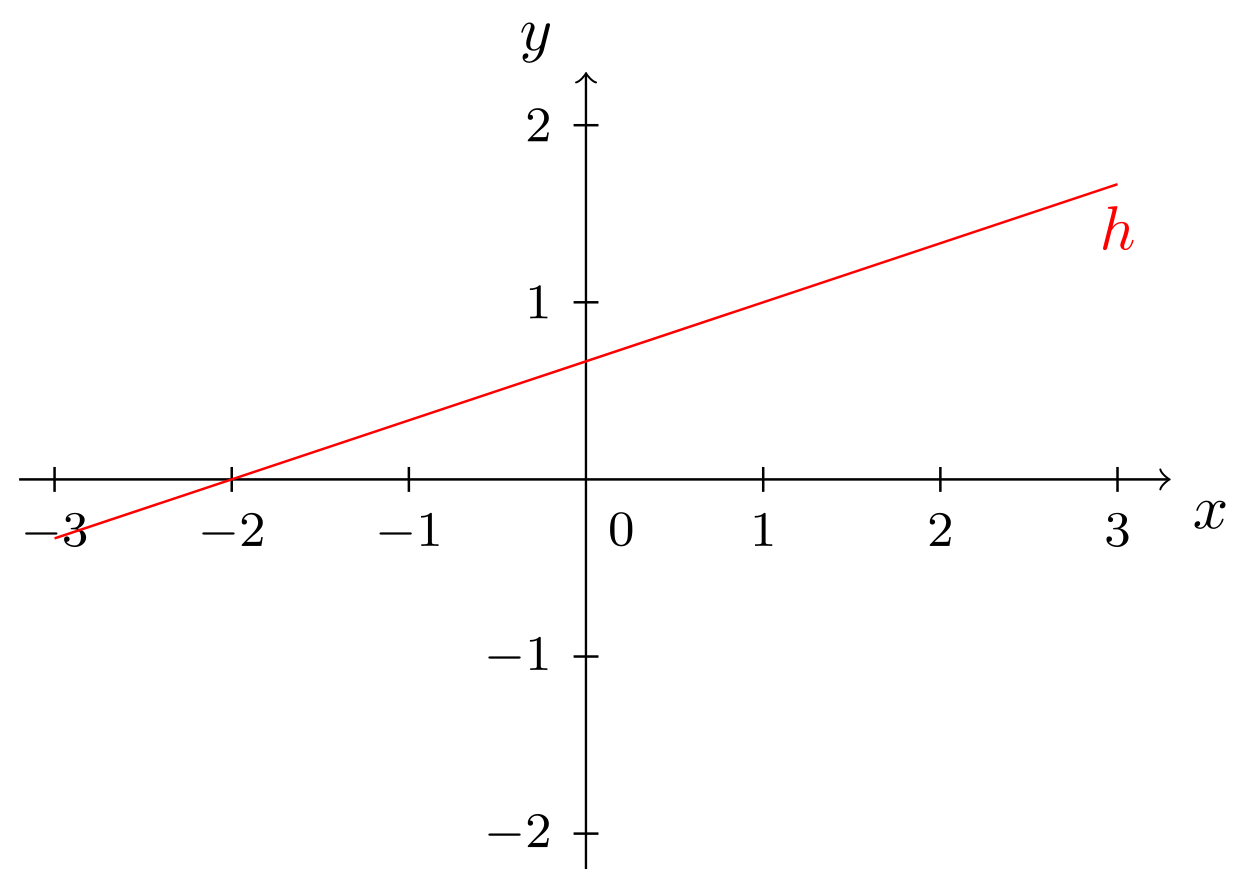
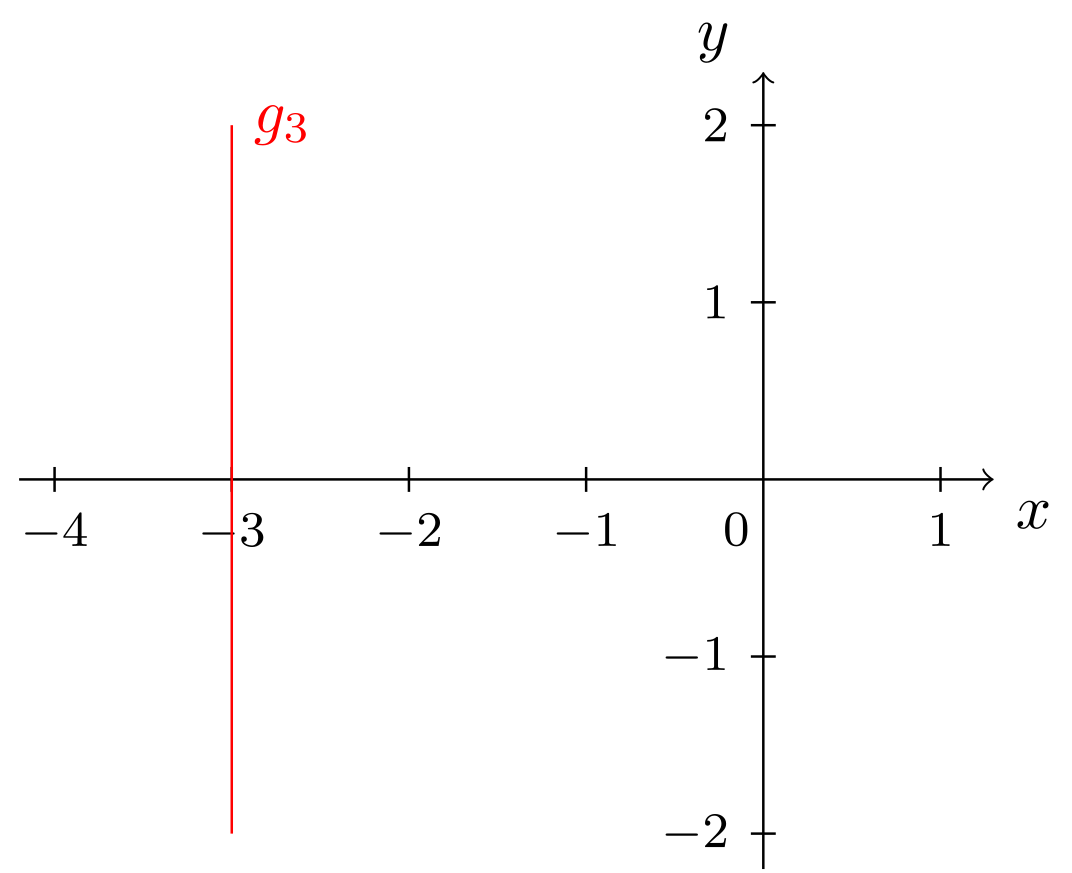
Das folgende Beispiel zeigt einige Geraden und ihre Mengenbeschreibungen bzw. Geradengleichungen.
Ziel ist es nun eine Gerade, welche durch eine Geradengleichung oder andere Daten eindeutig festgelegt ist, in einem Koordinatensystem im korrekt einzeichnen zu können. Hierfür wird noch ein genauerer Zusammenhang zu den Graphen linear-affiner Funktionen benötigt. Außerdem muss man wissen, durch welche Arten von Daten eine Gerade in der Ebene eindeutig festgelegt ist. Dies wird im Folgenden vorgestellt.
Info
9.2.4
Eine Gerade , gegeben durch eine Geradengleichung in Koordinatenform
kann in Normalform angegeben werden, falls gilt. Denn dann lässt sich die Geradengleichung nach auflösen und die Normalform von lautet
In dieser Form beschreibt die Gerade den Graphen einer linear-affinen Funktion mit Steigung und Achsenabschnitt :
Eine Gerade , gegeben durch eine Geradengleichung in Koordinatenform
kann in Normalform angegeben werden, falls gilt. Denn dann lässt sich die Geradengleichung nach auflösen und die Normalform von lautet
In dieser Form beschreibt die Gerade den Graphen einer linear-affinen Funktion mit Steigung und Achsenabschnitt :
Da man in der Normalform einer Geraden ihre Steigung und ihren Achsenabschnitt ablesen kann, kann man diese so wie die Graphen linear-affiner Funktionen zeichnen.
Beispiel
9.2.5
Die Gerade
besitzt die Geradengleichung in Koordinatenform. Durch Äquivalenzumformungen linearer Gleichungen kann diese auf die Form gebracht werden. Somit hat die Normalform
und beschreibt dadurch den Graphen der linear-affinen Funktion
mit der Steigung und dem Achsenabschnitt .
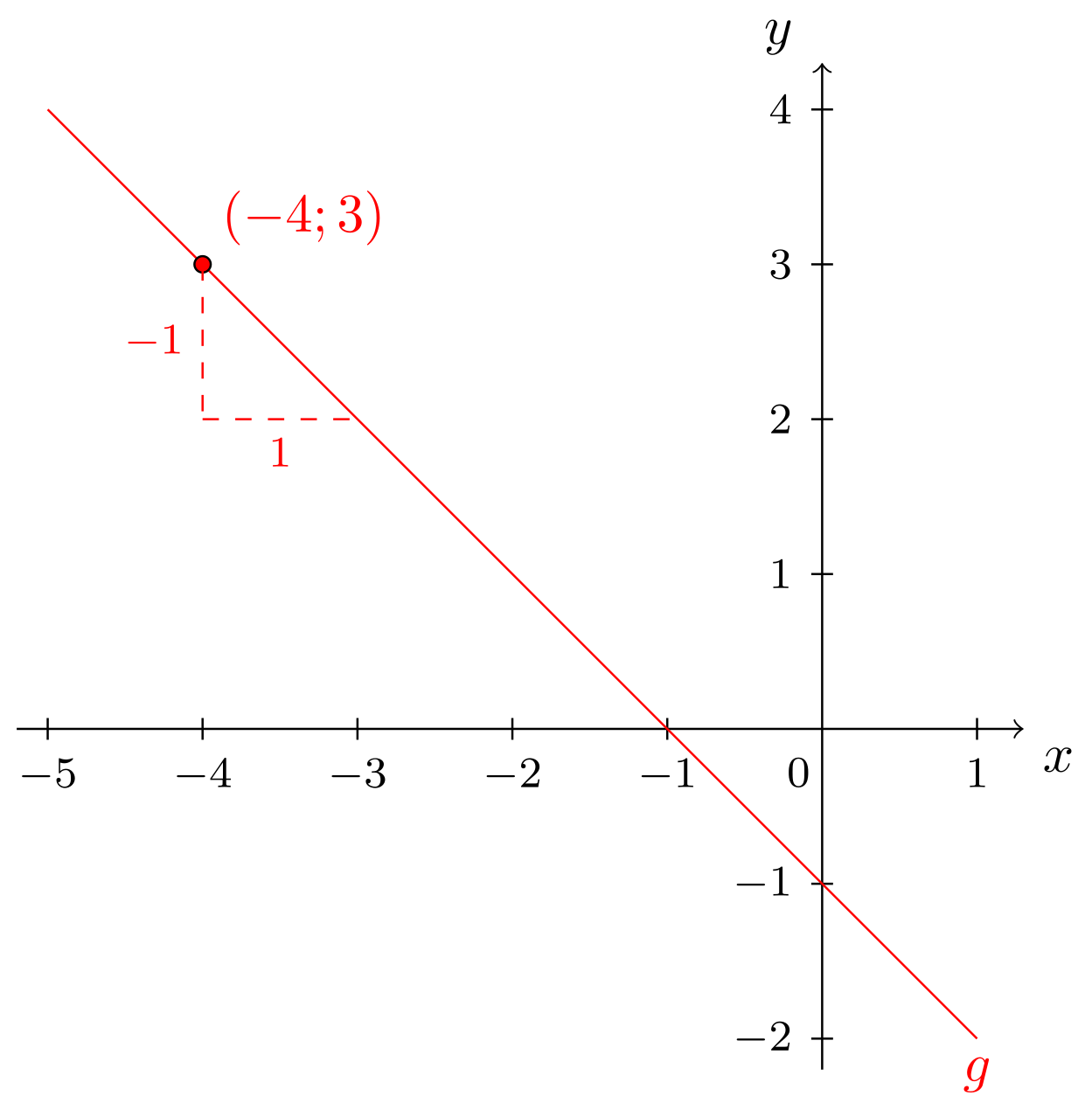
Um zu zeichnen, mache man sich Folgendes klar: Der Achsenabschnitt impliziert, dass den Punkt beinhaltet. Ausgehend von diesem Punkt kann durch das Anlegen eines Steigungsdreiecks der Steigung (um nach rechts und um nach unten) in der korrekten Richtung gezeichnet werden:
Die Gerade
besitzt die Geradengleichung in Koordinatenform. Durch Äquivalenzumformungen linearer Gleichungen kann diese auf die Form gebracht werden. Somit hat die Normalform
und beschreibt dadurch den Graphen der linear-affinen Funktion
mit der Steigung und dem Achsenabschnitt .
Um zu zeichnen, mache man sich Folgendes klar: Der Achsenabschnitt impliziert, dass den Punkt beinhaltet. Ausgehend von diesem Punkt kann durch das Anlegen eines Steigungsdreiecks der Steigung (um nach rechts und um nach unten) in der korrekten Richtung gezeichnet werden:

Abbildung 9.2.7: Skizze (C)
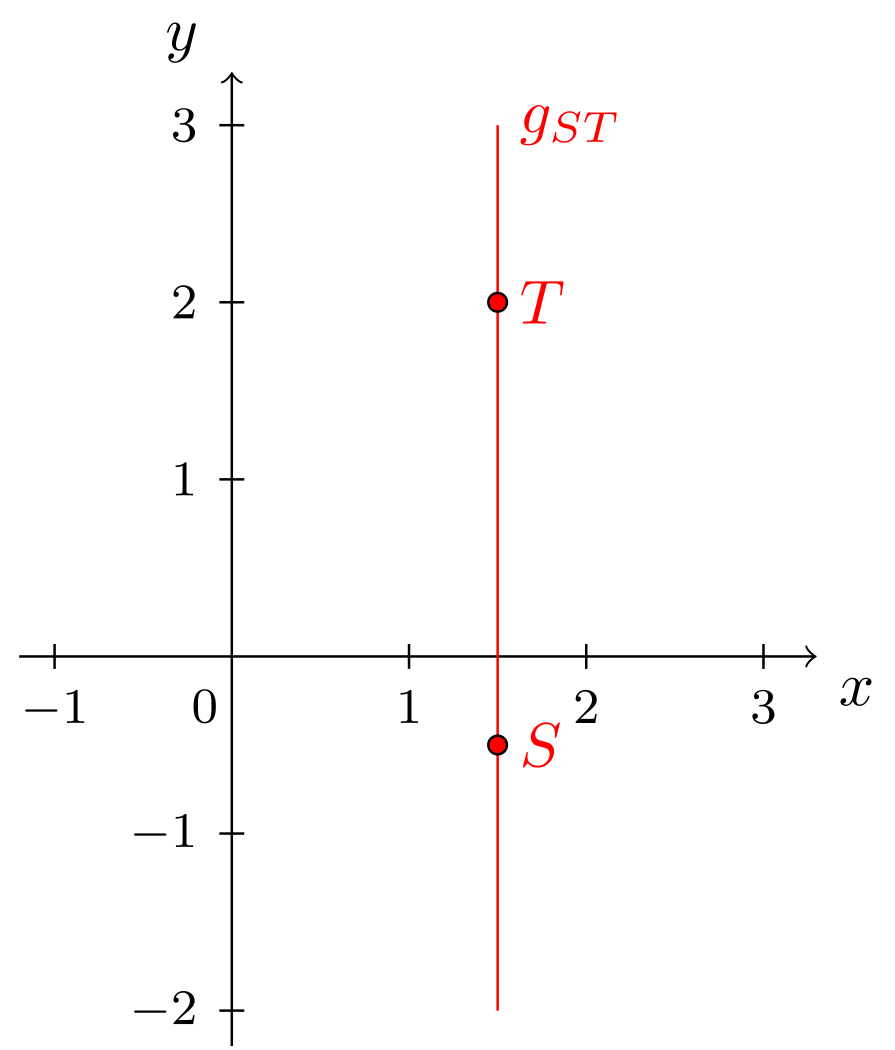
An dieser Stelle sind nun zwei Besonderheiten zu beachten. Diese zeigen sich am Beispiel der beiden Geraden und aus Beispiel 9.2.3:
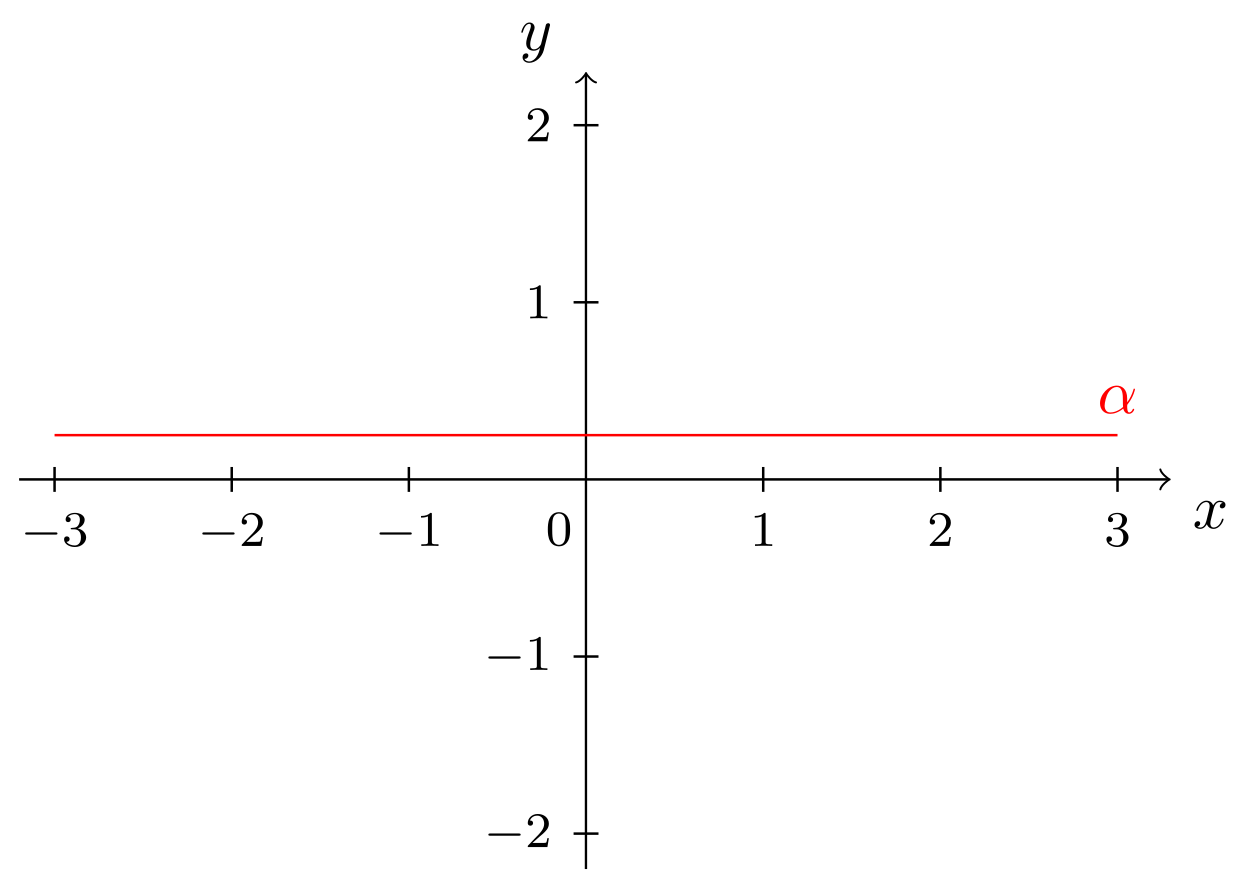
Abbildung 9.2.8: Skizze (C)
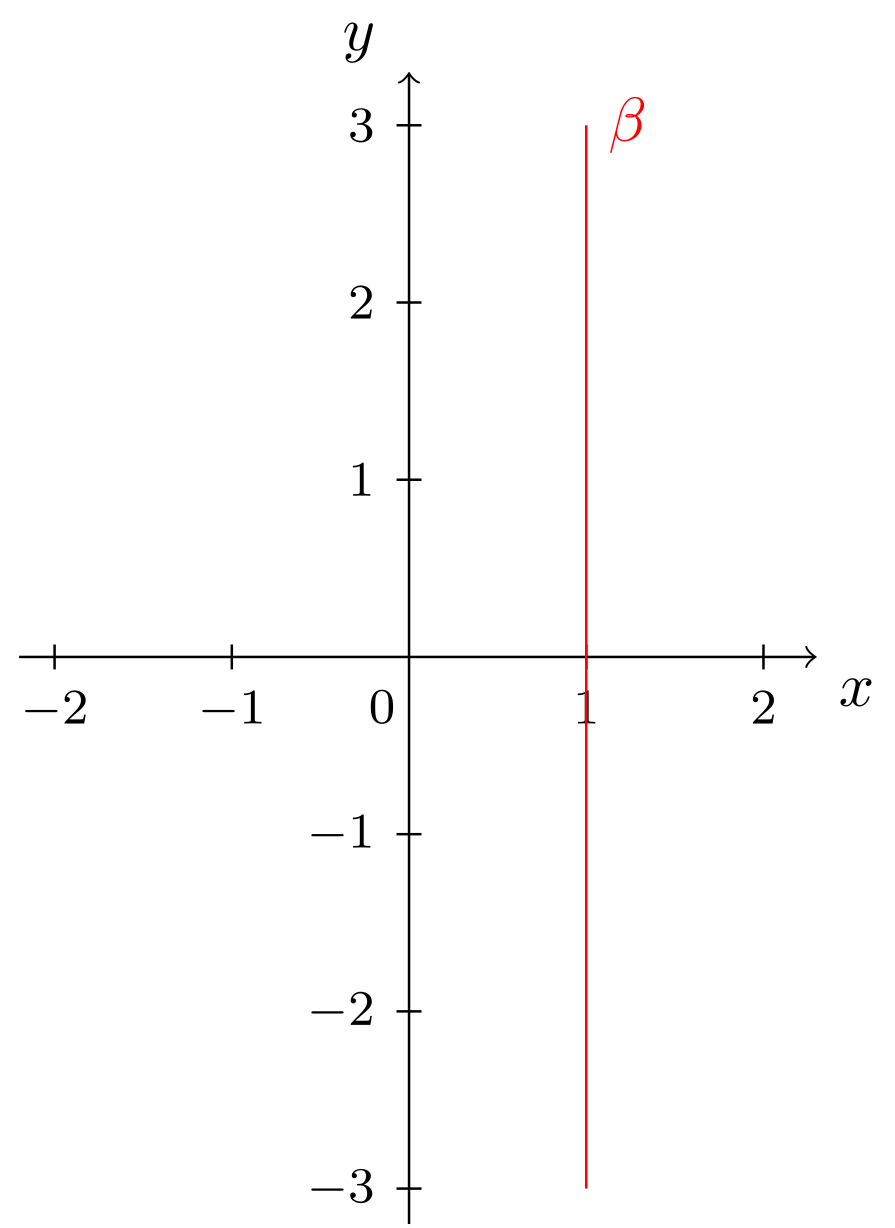
Abbildung 9.2.9: Skizze (C)
Die Gerade ist parallel zur -Achse. Ihre Normalform beschreibt also den Graphen einer konstanten Funktion, als Spezialfall der linear-affinen Funktionen. Die Gerade ist parallel zur -Achse. Ihre Geradengleichung erfüllt nicht die Voraussetzungen, um auf Normalform gebracht werden zu können. Dies trifft auf alle Geraden zu, die parallel zur -Achse verlaufen. Für solche Geraden gibt es also keine Normalform, da sie nicht durch den Graphen einer Funktion beschrieben werden können (vgl. 6.1.4). Weiterhin besitzen Geraden parallel zur -Achse auch keinen Achsenabschnitt, da sie die -Achse nicht schneiden. Auch eine Steigung besitzen solche Geraden eigentlich nicht, man kann ihnen aber aus Konsistenzgründen die Steigung zuordnen.
Aufgabe 9.2.6
Zeichnen Sie die folgenden Geraden in ein Koordinatensystem ein. Bringen Sie die Geradengleichung (falls möglich und nötig) jeweils zunächst auf Normalform.
Zeichnen Sie die folgenden Geraden in ein Koordinatensystem ein. Bringen Sie die Geradengleichung (falls möglich und nötig) jeweils zunächst auf Normalform.
Aufgabe 9.2.7
Gegeben sei eine Gerade durch folgendes Bild:

Geben Sie die Geradengleichung von in Normalform an.

Gegeben sei eine Gerade durch folgendes Bild:

Abbildung 9.2.13: Skizze (C)
Geben Sie die Geradengleichung von in Normalform an.
Außer mittels einer Geradengleichung, kann eine bestimmte Gerade in der Ebene auch durch andere Daten eindeutig festgelegt werden. Aus diesen Daten kann man die zugehörige Geradengleichung ermitteln und die entsprechende Gerade in ein Koordinatensystem einzeichnen.
Info
9.2.8
Für eine Gerade in der Ebene gilt:
Für eine Gerade in der Ebene gilt:
- „Zwei Punkte legen eine Gerade eindeutig fest“: Sind zwei Punkte und im gegeben, so gibt es genau eine Gerade , welche durch und verläuft. Man schreibt dann auch oder einfach für die Gerade durch und .
- „Ein Punkt und eine Steigung legen eine Gerade eindeutig fest“: Ist ein Punkt und eine Steigung gegeben, so gibt es genau eine Gerade , welche durch verläuft und die Steigung besitzt.
Die folgenden beiden Beispiele zeigen, wie aus Daten, die eine Gerade eindeutig festlegen, die entsprechende Geradengleichung ermittelt und die Gerade gezeichnet werden kann.
Beispiel
9.2.9
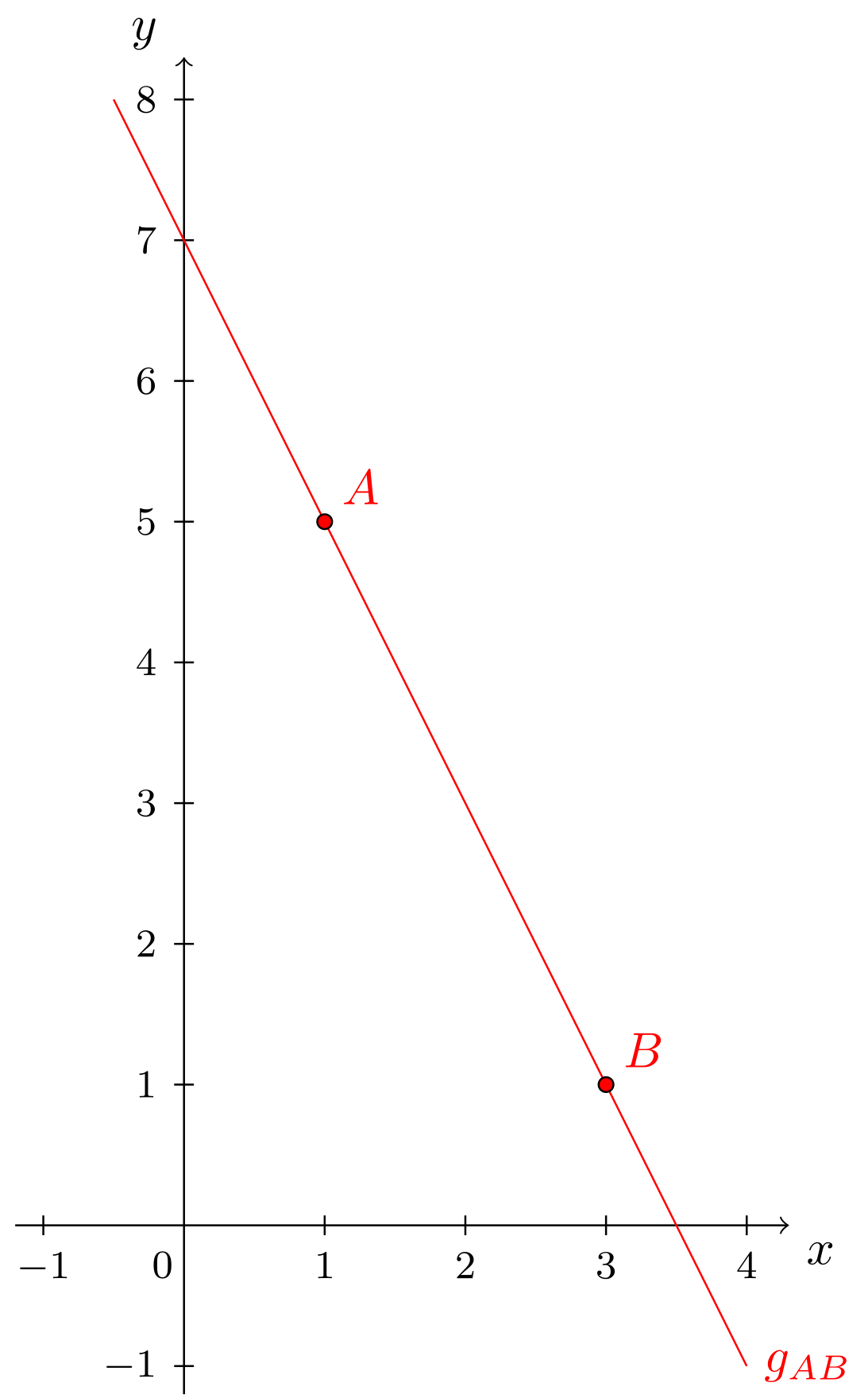
Gegeben sind die Punkte und . Die Gerade durch diese beiden Punkte kann direkt gezeichnet werden. Zur Ermittlung der Geradengleichung ist es nützlich, die beiden gegebenen Punkte zur Konstruktion eines Steigungsdreiecks zu nutzen:
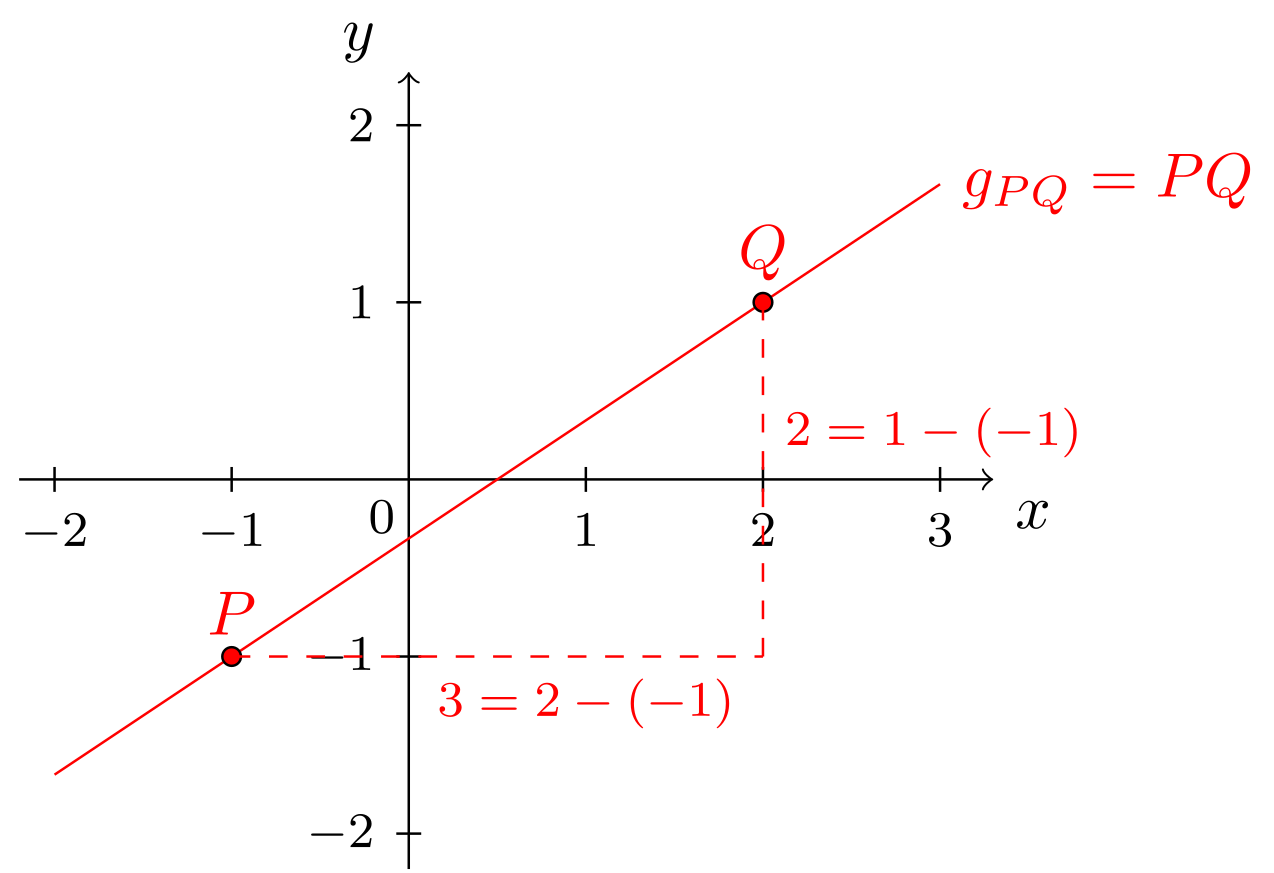
Aus den -Koordinaten und von und ergibt sich die Breite des Steigungsdreiecks und aus den entsprechenden -Koordinaten und die Höhe . Damit ist die Steigung der Gerade . Man erhält nun die Geradengleichung von in Normalform:
Es wird nur noch der Achsenabschnitt benötigt. Hierfür nutzt man aus, dass durch die beiden Punkte und verläuft. Man setzt die - und -Koordinaten eines der beiden Punkte in die Geradengleichung ein und berechnet . Benutzt man zum Beispiel den Punkt erhält man
Benutzung des Punktes würde auf das gleiche Ergebnis führen. Somit lautet die gesuchte Geradengleichung in Normalform
Gegeben sind die Punkte und . Die Gerade durch diese beiden Punkte kann direkt gezeichnet werden. Zur Ermittlung der Geradengleichung ist es nützlich, die beiden gegebenen Punkte zur Konstruktion eines Steigungsdreiecks zu nutzen:

Abbildung 9.2.14: Skizze (C)
Aus den -Koordinaten und von und ergibt sich die Breite des Steigungsdreiecks und aus den entsprechenden -Koordinaten und die Höhe . Damit ist die Steigung der Gerade . Man erhält nun die Geradengleichung von in Normalform:
Es wird nur noch der Achsenabschnitt benötigt. Hierfür nutzt man aus, dass durch die beiden Punkte und verläuft. Man setzt die - und -Koordinaten eines der beiden Punkte in die Geradengleichung ein und berechnet . Benutzt man zum Beispiel den Punkt erhält man
Benutzung des Punktes würde auf das gleiche Ergebnis führen. Somit lautet die gesuchte Geradengleichung in Normalform
Beispiel
9.2.10
Gegeben ist der Punkt und die Steigung . Gesucht ist die Gerade , welche durch verläuft und die Steigung besitzt. Analog wie in Beispiel 9.2.9 oben kann hier die Normalform der Geradengleichung von mit noch unbekanntem Achsenabschnitt direkt angegeben werden:
Weiterhin sind hier nun - und -Koordinaten des Punktes gegeben, aus welchen - ebenfalls wie in Beispiel 9.2.9 oben - der Achsenabschnitt berechnet werden kann:
Somit lautet die gesuchte Geradengleichung
Aus dem Punkt und der Steigung kann auch sofort gezeichnet werden, wie das folgende Bild veranschaulicht:
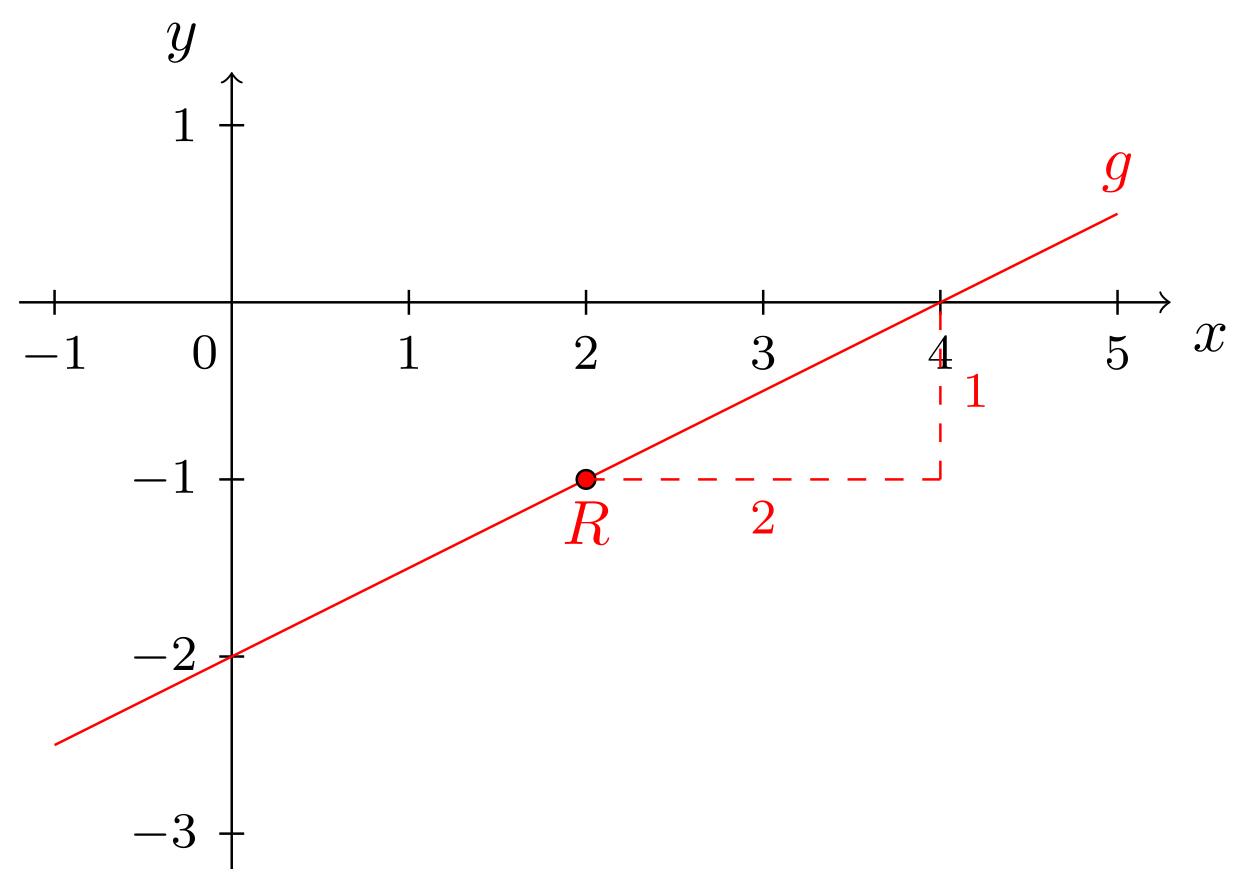
Gegeben ist der Punkt und die Steigung . Gesucht ist die Gerade , welche durch verläuft und die Steigung besitzt. Analog wie in Beispiel 9.2.9 oben kann hier die Normalform der Geradengleichung von mit noch unbekanntem Achsenabschnitt direkt angegeben werden:
Weiterhin sind hier nun - und -Koordinaten des Punktes gegeben, aus welchen - ebenfalls wie in Beispiel 9.2.9 oben - der Achsenabschnitt berechnet werden kann:
Somit lautet die gesuchte Geradengleichung
Aus dem Punkt und der Steigung kann auch sofort gezeichnet werden, wie das folgende Bild veranschaulicht:

Abbildung 9.2.15: Skizze (C)
Aufgabe 9.2.11
Geben Sie jeweils die gesuchten Geradengleichungen an und zeichnen Sie jeweils die Geraden.
Geben Sie jeweils die gesuchten Geradengleichungen an und zeichnen Sie jeweils die Geraden.
- Gegeben sind die Punkte und .

- Gegeben sind die Punkte und .

- Gesucht ist die Gleichung der Gerade durch den Punkt mit der Steigung .

- Gesucht ist die Gleichung der Gerade durch den Punkt mit der Steigung .