10.1.4 Rechnen mit Vektoren
In diesem Abschnitt wird behandelt, wie man mit den - im vorigen Abschnitt 10.1.3 eingeführten - Vektoren rechnen kann. Das Rechnen mit Vektoren hat mehrere Aspekte: Zunächst kann man mit Vektoren, die man als 2- oder 3-Tupel angibt, die Rechenoperationen Addition, Subtraktion und - mit einer gewissen Einschränkung - auch Multiplikation durchführen, indem man diese Operationen komponentenweise ausführt. Dann haben diese Rechenoperationen aber auch eine geometrische Bedeutung für die Pfeile, welche die Vektoren repräsentieren. Man kann die Rechenoperationen für Vektoren auch als geometrische Operationen mit ihren Repräsentanten interpretieren. Schließlich führt diese geometrische Betrachtung des Rechnens mit Vektoren auch auf ein tieferes Verständnis von Orts- und Verbindungsvektoren von Punkten.
Das Rechnen mit zwei- und dreidimensionalen Vektoren funktioniert im Wesentlichen auf die gleiche Art und Weise. Bei den Rechenoperationen in Komponentenschreibweise werden im Folgenden immer beide Fälle (zwei- und dreidimensional) aufgeführt. Bei den zugehörigen Bildern, welche die geometrische Bedeutung der Operationen für die Repräsentanten der Vektoren sowie für Orts- und Verbindungsvektoren veranschaulichen, werden in diesem Abschnitt nur Pfeile und Punkte, keine Koordinatensysteme dargestellt. So sind diese Bilder sowohl für den zwei- als auch für den dreidimensionalen Fall gültig.
Da beim Rechnen mit Vektoren im Folgenden Vektoren durch Rechnung und Äquivalenzumformungen auseinander hervorgehen sollen, muss einmal festgehalten werden, unter welchen Umständen zwei Vektoren gleich sein sollen.
Diese Infobox macht auch klar, dass zwei Vektoren unterschiedlicher Dimension (also etwa und ) niemals gleich sein können. Diese Vektoren sind wegen der unterschiedlichen Anzahl an Komponenten sogar nicht einmal miteinander vergleichbar. Rechnungen mit Vektoren finden also immer nur mit einer festen Anzahl an Komponenten statt (hier entweder zwei oder drei), und die Ergebnisse der Rechnungen sind dann immer auch Vektoren mit ebendieser festen Anzahl an Komponenten.
Auch bei der Addition von Vektoren gilt, analog zum Rechnen mit reellen Zahlen, das Kommutativ- und das Assoziativgesetz (vgl. Abschnitt 1.1.3)
sowie
Und der Nullvektor bzw. erfüllt die analoge Funktion für Vektoren, die die für reelle Zahlen erfüllt:
Das obige Beispiel zeigt, dass man mit Hilfe der Vektorrechnung auch Ausdrücke für Verbindungsvektoren von Punkten vereinfachen kann. Dies wird weiter unten bei der Subtraktion von Vektoren nochmals vertieft.
Das Rechnen mit zwei- und dreidimensionalen Vektoren funktioniert im Wesentlichen auf die gleiche Art und Weise. Bei den Rechenoperationen in Komponentenschreibweise werden im Folgenden immer beide Fälle (zwei- und dreidimensional) aufgeführt. Bei den zugehörigen Bildern, welche die geometrische Bedeutung der Operationen für die Repräsentanten der Vektoren sowie für Orts- und Verbindungsvektoren veranschaulichen, werden in diesem Abschnitt nur Pfeile und Punkte, keine Koordinatensysteme dargestellt. So sind diese Bilder sowohl für den zwei- als auch für den dreidimensionalen Fall gültig.
Da beim Rechnen mit Vektoren im Folgenden Vektoren durch Rechnung und Äquivalenzumformungen auseinander hervorgehen sollen, muss einmal festgehalten werden, unter welchen Umständen zwei Vektoren gleich sein sollen.
Info
10.1.8
Zwei Vektoren sind genau dann gleich (symbolisch: ), wenn eine (und damit alle) der folgenden äquivalenten Bedingungen zutrifft (zutreffen):
Zwei Vektoren sind genau dann gleich (symbolisch: ), wenn eine (und damit alle) der folgenden äquivalenten Bedingungen zutrifft (zutreffen):
- und besitzen die gleichen Komponenten, also
im zweidimensionalen Fall bzw.
im dreidimensionalen Fall. Dies ist auch unter der Bezeichnung Koordinaten- oder Komponentenvergleich bekannt.
- und besitzen einen gleichen Repräsentanten.
- und sind beide Ortsvektor des gleichen Punktes.
- und sind beide Verbindungsvektor der gleichen zwei Punkte.
Diese Infobox macht auch klar, dass zwei Vektoren unterschiedlicher Dimension (also etwa und ) niemals gleich sein können. Diese Vektoren sind wegen der unterschiedlichen Anzahl an Komponenten sogar nicht einmal miteinander vergleichbar. Rechnungen mit Vektoren finden also immer nur mit einer festen Anzahl an Komponenten statt (hier entweder zwei oder drei), und die Ergebnisse der Rechnungen sind dann immer auch Vektoren mit ebendieser festen Anzahl an Komponenten.
Info
10.1.9
Die Addition zweier Vektoren bedeutet die Addition aller ihrer Komponenten. Also
im zweidimensionalen Fall und
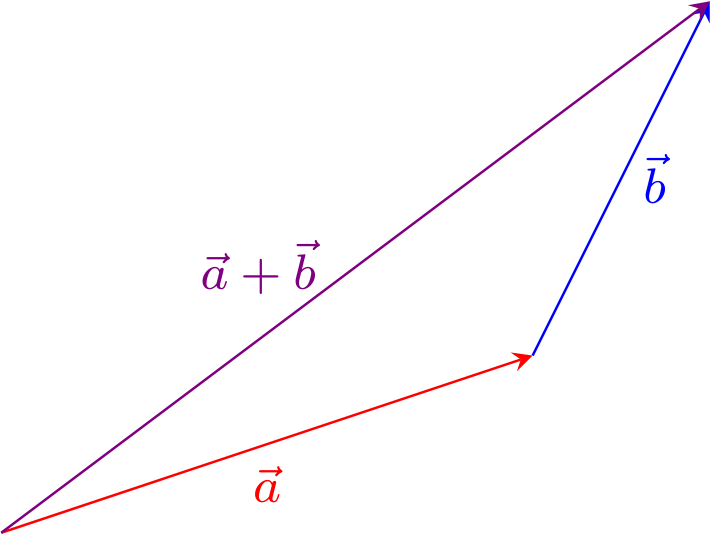
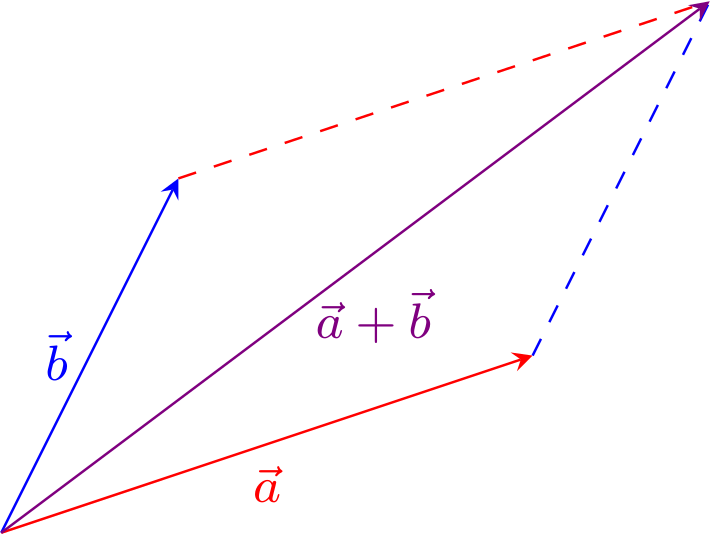
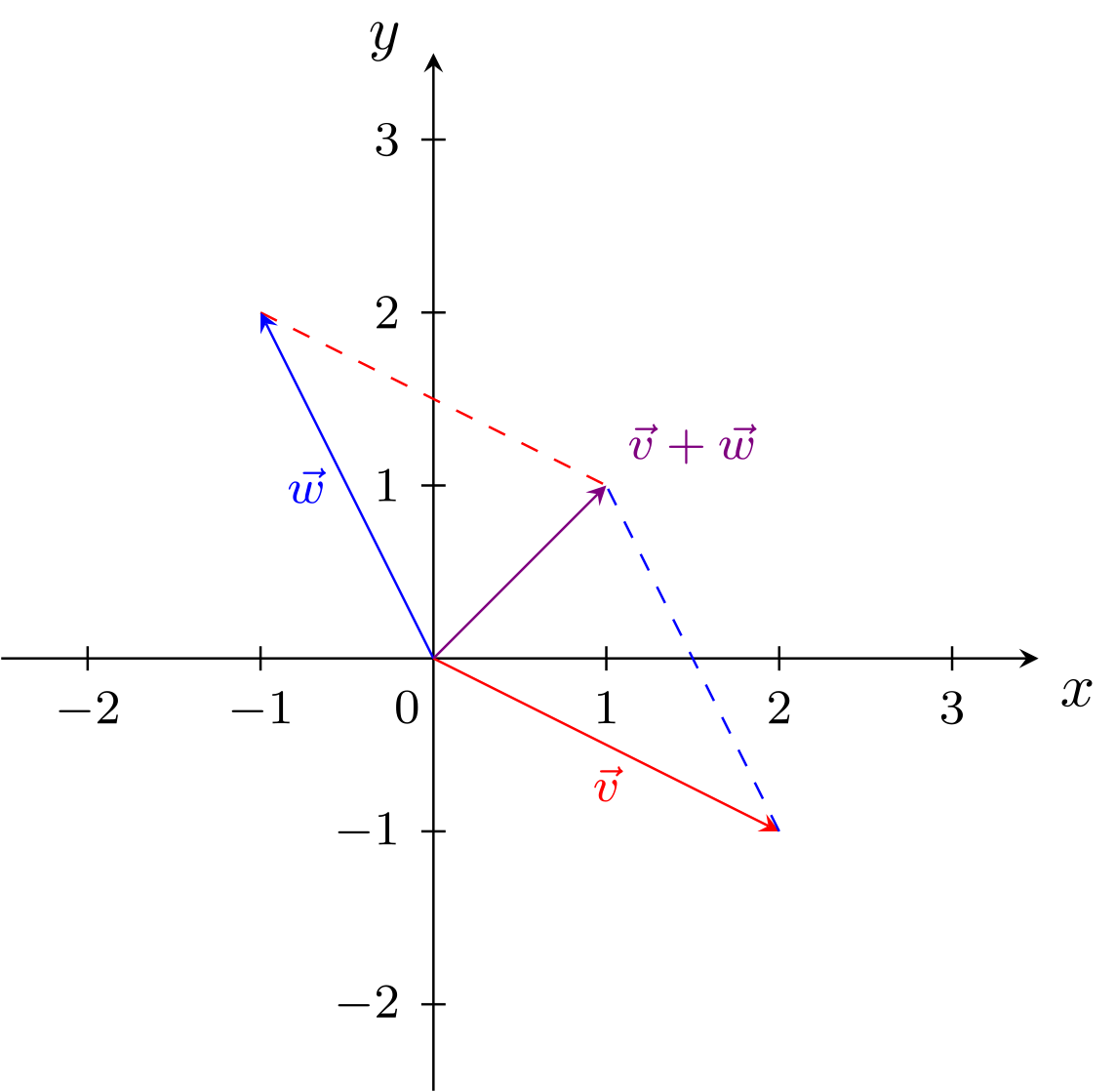
im dreidimensionalen Fall. Geometrisch kann die Vektoraddition als „Aneinanderhängen“ von Pfeilen oder als Ergänzung von zwei Pfeilen zu einem Parallelogramm interpretiert werden, je nachdem welche Repräsentanten der Vektoren man verwendet:
Die Addition zweier Vektoren bedeutet die Addition aller ihrer Komponenten. Also
im zweidimensionalen Fall und
im dreidimensionalen Fall. Geometrisch kann die Vektoraddition als „Aneinanderhängen“ von Pfeilen oder als Ergänzung von zwei Pfeilen zu einem Parallelogramm interpretiert werden, je nachdem welche Repräsentanten der Vektoren man verwendet:
Auch bei der Addition von Vektoren gilt, analog zum Rechnen mit reellen Zahlen, das Kommutativ- und das Assoziativgesetz (vgl. Abschnitt 1.1.3)
sowie
Und der Nullvektor bzw. erfüllt die analoge Funktion für Vektoren, die die für reelle Zahlen erfüllt:
Aufgabe 10.1.11
- Gegeben sind die Vektoren und . Berechnen Sie .

- Gegeben sind die Punkte , und . Welche der folgenden Ausdrücke sind gleich dem Ausdruck ?
Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Richtig  Falsch
Falsch

Untersucht man mögliche Rechenoperationen für Vektoren nun weiter, so stellt man fest, dass die komponentenweise Multiplikation oder Division von Vektoren keine sinnvolle Operation ist. Dies genauer zu verstehen, würde aber den mathematischen Rahmen dieses Brückenkurses sprengen. So muss man an dieser Stelle einfach akzeptieren, dass man Vektoren nicht so einfach miteinander multiplizieren und schon gar nicht durcheinander dividieren kann. Was allerdings möglich ist, ist die Multiplikation von Vektoren mit reellen Zahlen und - darauf aufbauend - auch die Subtraktion von Vektoren. Wichtig ist noch Folgendes: Wird im Nachfolgenden von der Länge eines Vektors gesprochen, so ist damit die geometrische Länge der Pfeile gemeint, die ihn repräsentieren. Das Konzept der Länge oder des Betrags eines Vektors wird weiter unten noch genauer untersucht.
Info
10.1.12
Die Multiplikation eines Vektors mit einer reellen Zahl bedeutet die Multiplikation in jeder Komponente. Ist also ein Vektor und , so gilt
im zweidimensionalen Fall und
im dreidimensionalen Fall. Die Division eines Vektors durch eine Zahl ist dann einfach gegeben durch die Multiplikation mit dem Kehrwert :
Bei der Multiplikation eines Vektors mit einer reellen Zahl erhält man also einen gleich orientierten Vektor -facher Länge, wenn ist. Wenn ist, hat der resultierende Vektor ebenfalls -fache Länge, ist aber entgegengesetzt orientiert. Im Spezialfall , gilt offenbar
für jeden Vektor . Zwei weitere wichtige Fälle sind die Multiplikation mit :
- dies lässt den Vektor offenbar gleich - und die Multiplikation mit :
- dies ergibt den sogenannten Gegenvektor, ein Vektor gleicher Länge aber entgegengesetzter Orientierung. Bild hierzu:
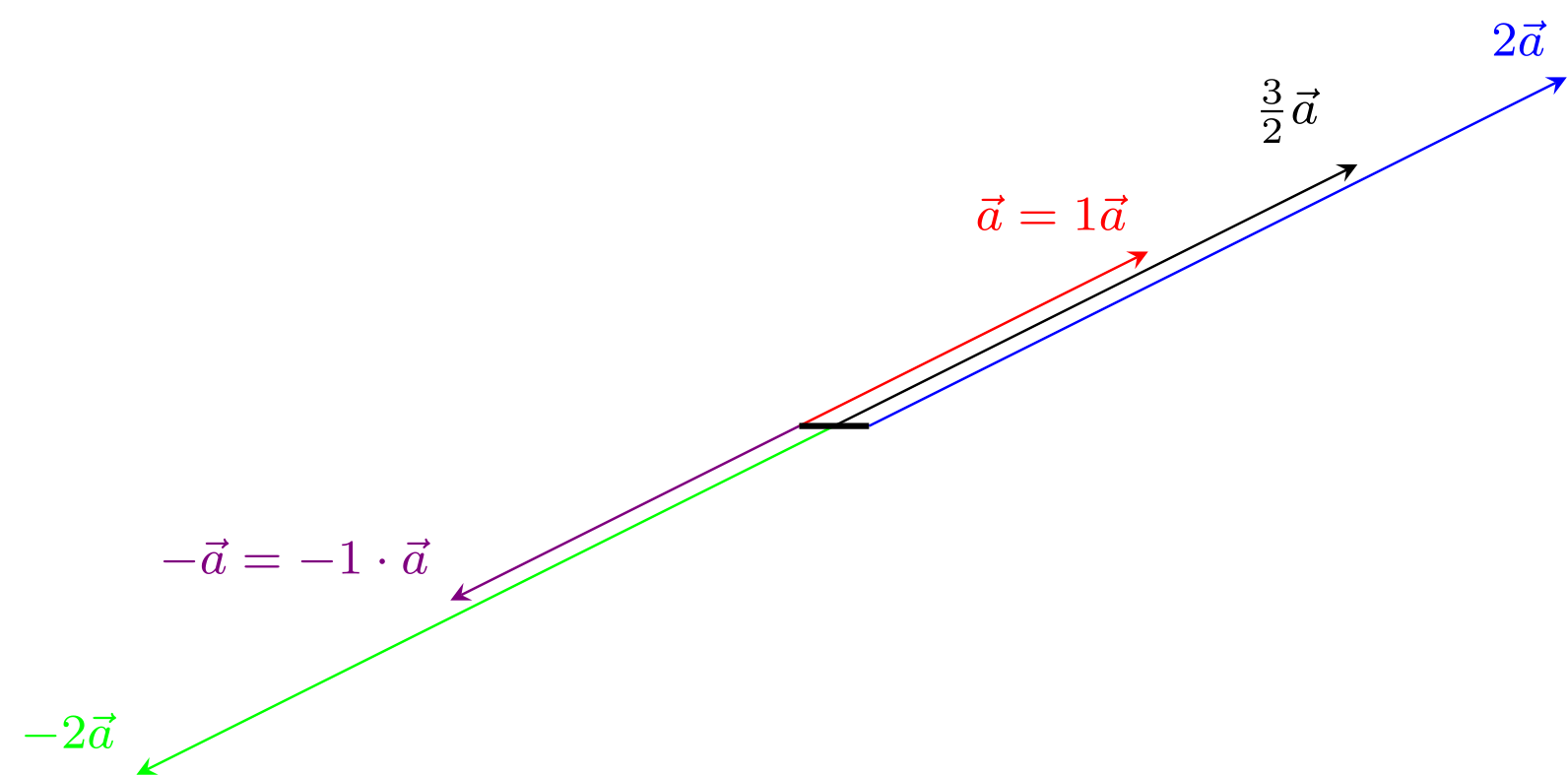
Da reelle Zahlen bei Multiplikation die Länge von Vektoren ändern, sie also skalieren, nennt man reelle Zahlen in Bezug auf Vektoren oft auch Skalare und spricht bei der Multiplikation einer reellen Zahl mit einem Vektor von Skalarmultiplikation.
Die Multiplikation eines Vektors mit einer reellen Zahl bedeutet die Multiplikation in jeder Komponente. Ist also ein Vektor und , so gilt
im zweidimensionalen Fall und
im dreidimensionalen Fall. Die Division eines Vektors durch eine Zahl ist dann einfach gegeben durch die Multiplikation mit dem Kehrwert :
Bei der Multiplikation eines Vektors mit einer reellen Zahl erhält man also einen gleich orientierten Vektor -facher Länge, wenn ist. Wenn ist, hat der resultierende Vektor ebenfalls -fache Länge, ist aber entgegengesetzt orientiert. Im Spezialfall , gilt offenbar
für jeden Vektor . Zwei weitere wichtige Fälle sind die Multiplikation mit :
- dies lässt den Vektor offenbar gleich - und die Multiplikation mit :
- dies ergibt den sogenannten Gegenvektor, ein Vektor gleicher Länge aber entgegengesetzter Orientierung. Bild hierzu:

Abbildung 10.1.15: Skizze (C)
Beispiel
10.1.13
Gegeben ist der Vektor . Dann gilt zum Beispiel
und
Außerdem gilt zum Beispiel für und , da
Dann ist aber
da
gilt. Bild dazu:
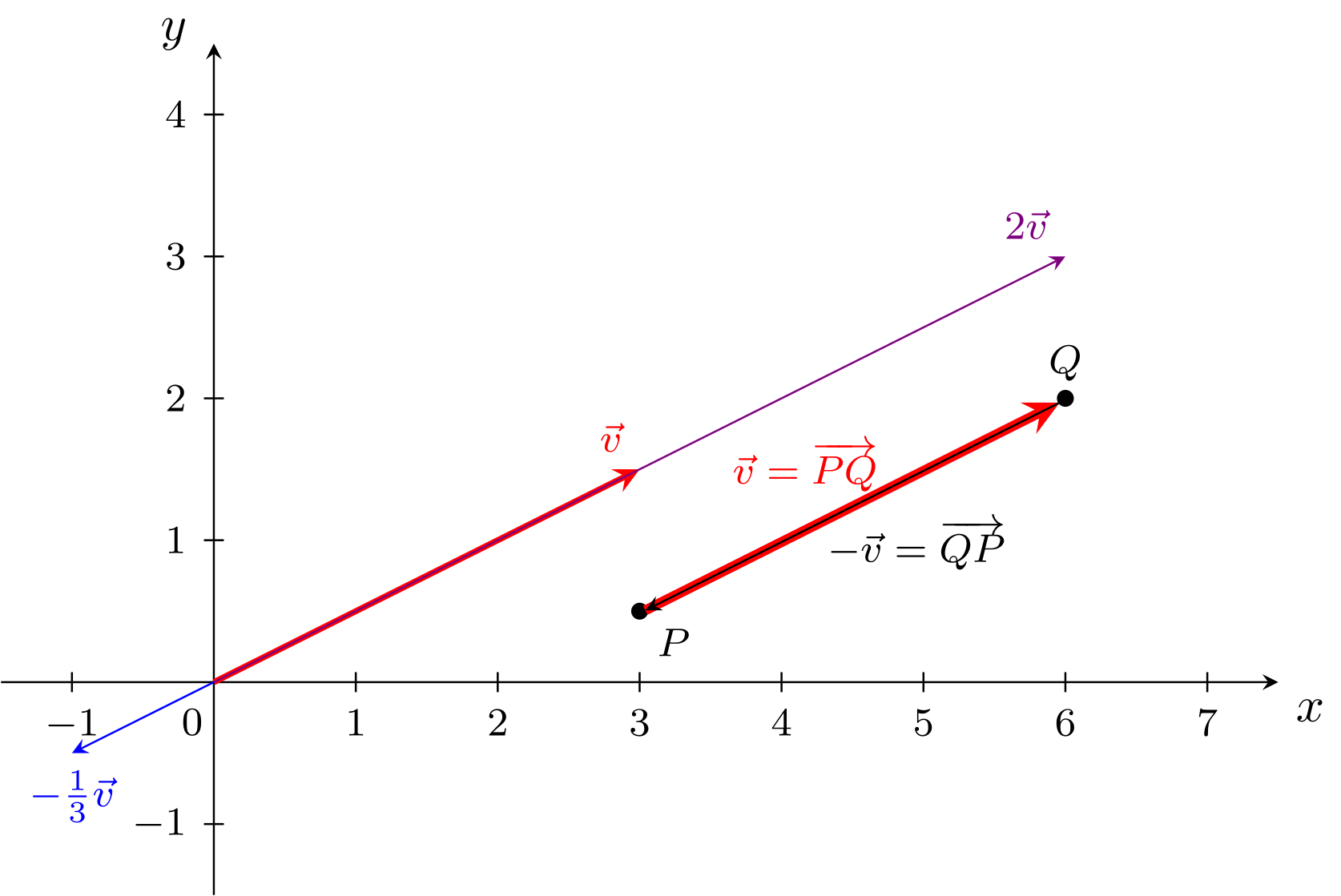
Gegeben ist der Vektor . Dann gilt zum Beispiel
und
Außerdem gilt zum Beispiel für und , da
Dann ist aber
da
gilt. Bild dazu:

Abbildung 10.1.16: Skizze (C)
Für das Rechnen mit Vielfachen von Vektoren gilt nun der folgende Satz von Rechengesetzen.
Info
10.1.14
Sind und reelle Zahlen sowie und Vektoren, so gelten die folgenden Rechengesetze:
Sind und reelle Zahlen sowie und Vektoren, so gelten die folgenden Rechengesetze:
-
-
-
-
-
- oder
Mit Hilfe des Konzeptes des Gegenvektors, kann nun auch festgehalten werden, was die Subtraktion von Vektoren bedeutet.
Info
10.1.15
Sind und Vektoren, so ist ihre Differenz gegeben als die Summe von und dem Gegenvektor von . Also gilt
im zweidimensionalen Fall und
im dreidimensionalen Fall. Damit kann die Differenz von Vektoren auch geometrisch mit Hilfe ihrer Repräsentanten interpretiert werden:
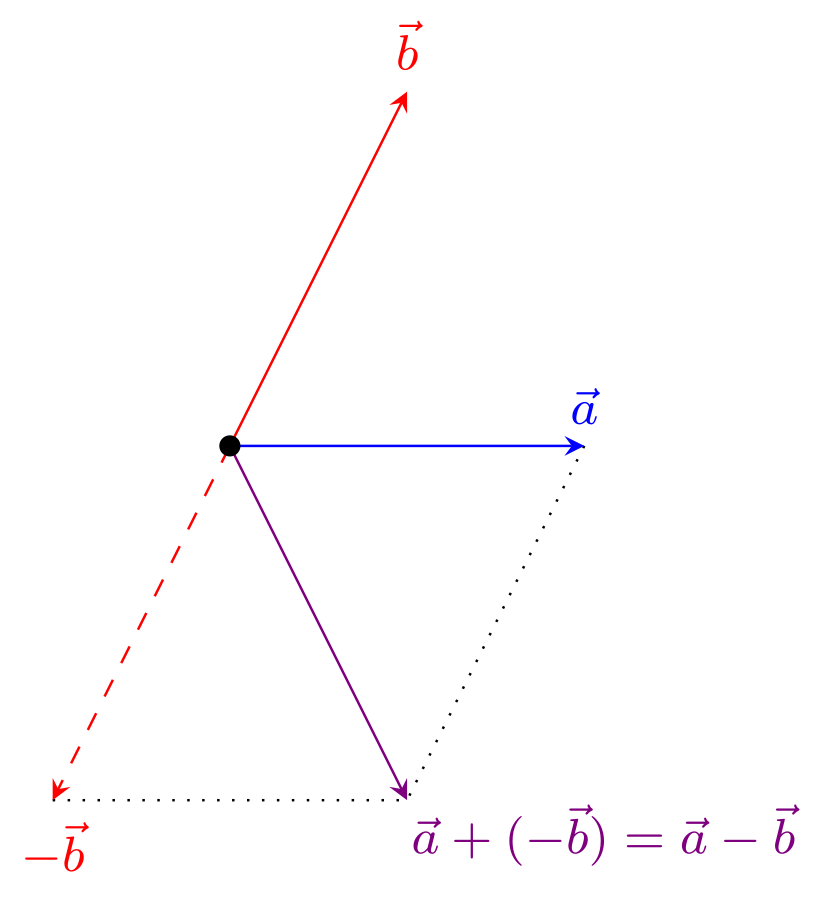
Sind und Vektoren, so ist ihre Differenz gegeben als die Summe von und dem Gegenvektor von . Also gilt
im zweidimensionalen Fall und
im dreidimensionalen Fall. Damit kann die Differenz von Vektoren auch geometrisch mit Hilfe ihrer Repräsentanten interpretiert werden:

Abbildung 10.1.17: Skizze (C)
Betrachtet man in dieser Infobox nur die Differenz von Vektoren anhand ihrer Komponenten, so kann man sich fragen, wozu hierfür überhaupt das Konzept des Gegenvektors notwendig ist. Tatsächlich könnte man die Differenz von Vektoren in Komponenten auch ohne die Idee des Gegenvektors in Analogie zur Summe hinschreiben. Überlegt man sich dann aber die geometrische Interpretation der Differenz mit Hilfe von Repräsentanten (vgl. die Abbildung in der Infobox), so sieht man, dass dies nur mit Hilfe des Gegenvektors möglich ist.
Beispiel
10.1.16
Es werden in diesem Beispiel einige typische Aufgabenstellungen betrachtet, welche die bisher behandelten Rechengesetze für Vektoren beinhalten.
Es werden in diesem Beispiel einige typische Aufgabenstellungen betrachtet, welche die bisher behandelten Rechengesetze für Vektoren beinhalten.
- Es sind die folgenden Vektorausdrücke zu vereinfachen:
- ,
- für .
- ,
- Für und ist der unbekannte Vektor in der Gleichung
zu bestimmen.
Auflösen nach sowie Einsetzen von und ergibt:
- Unter Benutzung der Differenz von Vektoren soll der Verbindungsvektor zweier Punkte und mit Hilfe der Ortsvektoren und ausgedrückt werden. Es gilt:
Der Verbindungsvektor von einem Punkt zu einem Punkt ergibt sich also immer als die Differenz des Ortsvektor (zum Endpunkt des Verbindungsvektors) und des Ortsvektors (zum Anfangspunkt des Verbindungsvektors). Dies zeigt auch nochmals das folgende Bild und ein Vergleich mit der Rechenregel für Verbindungsvektoren aus 10.1.5: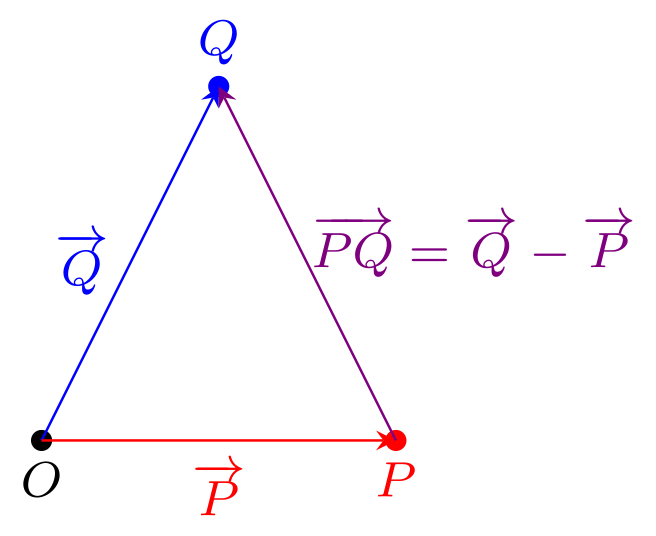 Abbildung 10.1.18: Skizze (C)
Abbildung 10.1.18: Skizze (C)
- Die Punkte , und bilden die Ecken eines Dreiecks. Der (geometrische) Schwerpunkt dieses Dreiecks kann mit Hilfe der zugehörigen Ortsvektoren berechnet werden:
Somit ist . Bild hierzu: Abbildung 10.1.19: Skizze (C)
Abbildung 10.1.19: Skizze (C)
Aufgabe 10.1.17
- Es sind , , und Punkte im Raum. Vereinfachen Sie den Ausdruck
so weit wie möglich.
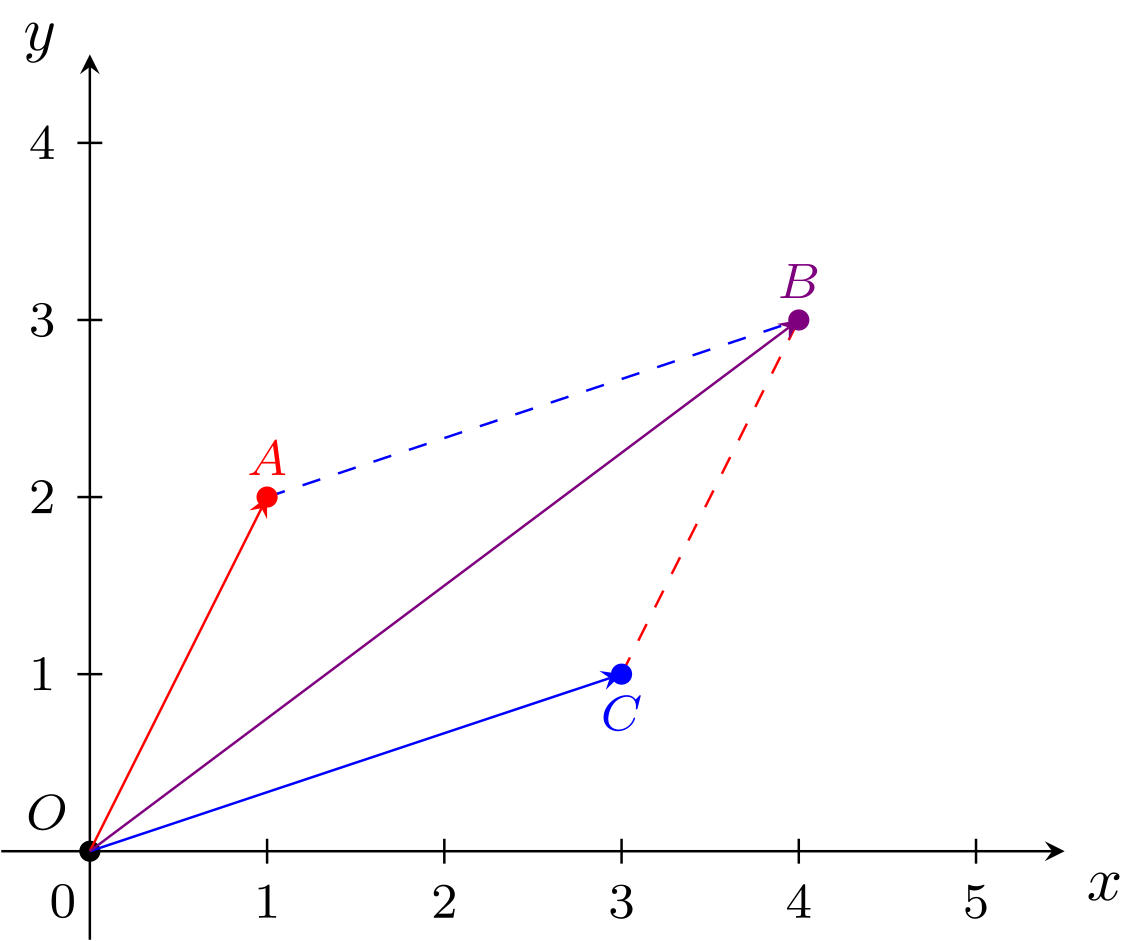
- Zeigen Sie, dass die Punkte , und zusammen mit dem Ursprung die Ecken eines Parallelogramms bilden.
Aufgabe 10.1.18
Vereinfachen Sie jeweils so weit wie möglich:
Vereinfachen Sie jeweils so weit wie möglich:
-
 .
.
-
 .
.
Aufgabe 10.1.19
Bestimmen Sie den Vektor in der Gleichung

Bestimmen Sie den Vektor in der Gleichung
Da Vektoren durch beliebig viele Pfeile repräsentiert werden, die alle durch Parallelverschiebung auseinander hervorgehen, haben alle diese Repräsentanten die gleiche geometrische Länge (nämlich immer den Abstand der beiden Punkte, die sie verbinden). Deshalb ist es auch sinnvoll von der Länge eines Vektors zu sprechen. Die Länge eines Vektors trägt in der Mathematik die Bezeichnung Betrag oder Norm.
Info
10.1.20
Der Betrag oder die Norm eines Vektors wird als geschrieben und ist der Abstand desjenigen Punktes vom Ursprung , zu dem der Vektor der zugehörige Ortsvektor ist (also ). Also gilt
und folglich im zweidimensionalen Fall
sowie im dreidimensionalen Fall
Ein Vektor mit Betrag wird auch Einheitsvektor genannt.
Der Betrag oder die Norm eines Vektors wird als geschrieben und ist der Abstand desjenigen Punktes vom Ursprung , zu dem der Vektor der zugehörige Ortsvektor ist (also ). Also gilt
und folglich im zweidimensionalen Fall
sowie im dreidimensionalen Fall
Ein Vektor mit Betrag wird auch Einheitsvektor genannt.
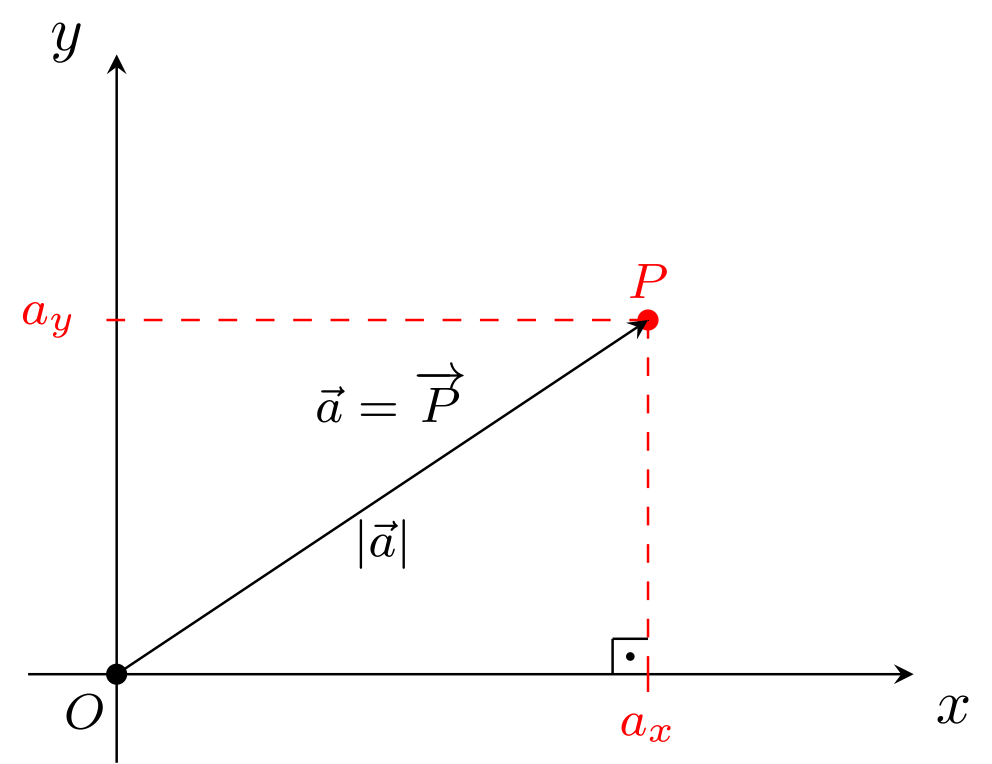
Abbildung 10.1.21: Skizze (C)
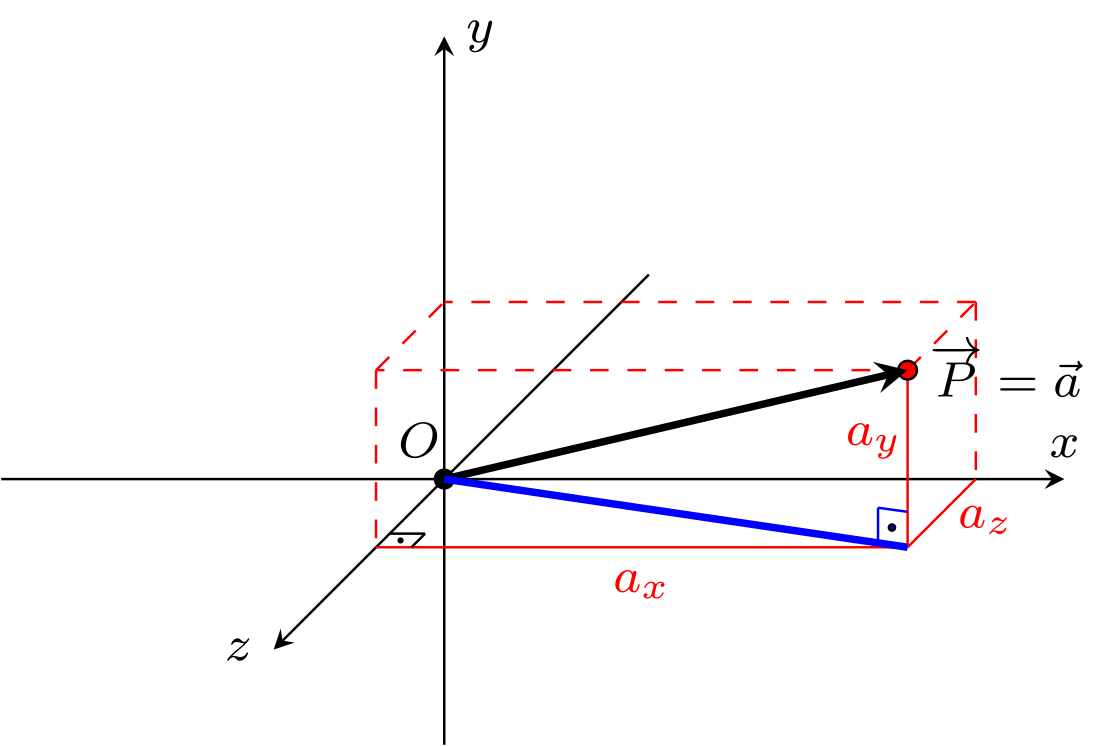
Abbildung 10.1.22: Skizze (C)
Für Normen von Vektoren gilt der folgende Satz von Rechenregeln.
Info
10.1.21
Sind und Vektoren (beide aus dem oder beide aus dem ) und ist , so gilt
Sind und Vektoren (beide aus dem oder beide aus dem ) und ist , so gilt
- und ,
- und
- .
Beispiel
10.1.22
- Der Betrag des Vektors berechnet sich zu
Es handelt sich also um einen Einheitsvektor.
- Es ist eine Zahl zu finden, so dass gilt.
Aufgabe 10.1.23
Berechnen Sie
 .
.
Berechnen Sie
Aufgabe 10.1.24
Finden Sie die Zahl , für die gilt:
 .
.
Finden Sie die Zahl , für die gilt:
Aufgabe 10.1.25
Zeigen Sie, dass die Punkte , und die Ecken eines gleichseitigen Dreiecks bilden.
Zeigen Sie, dass die Punkte , und die Ecken eines gleichseitigen Dreiecks bilden.