5.4.5 Flächeninhalt
Der Inhalt einer Fläche ist die Zahl der Einheitsquadrate, die man benötigt,
um diese Fläche vollständig zu bedecken.
Der Flächeninhalt des Dreiecks ist nun die Hälfte des Flächeninhaltes
des Rechtecks, also .
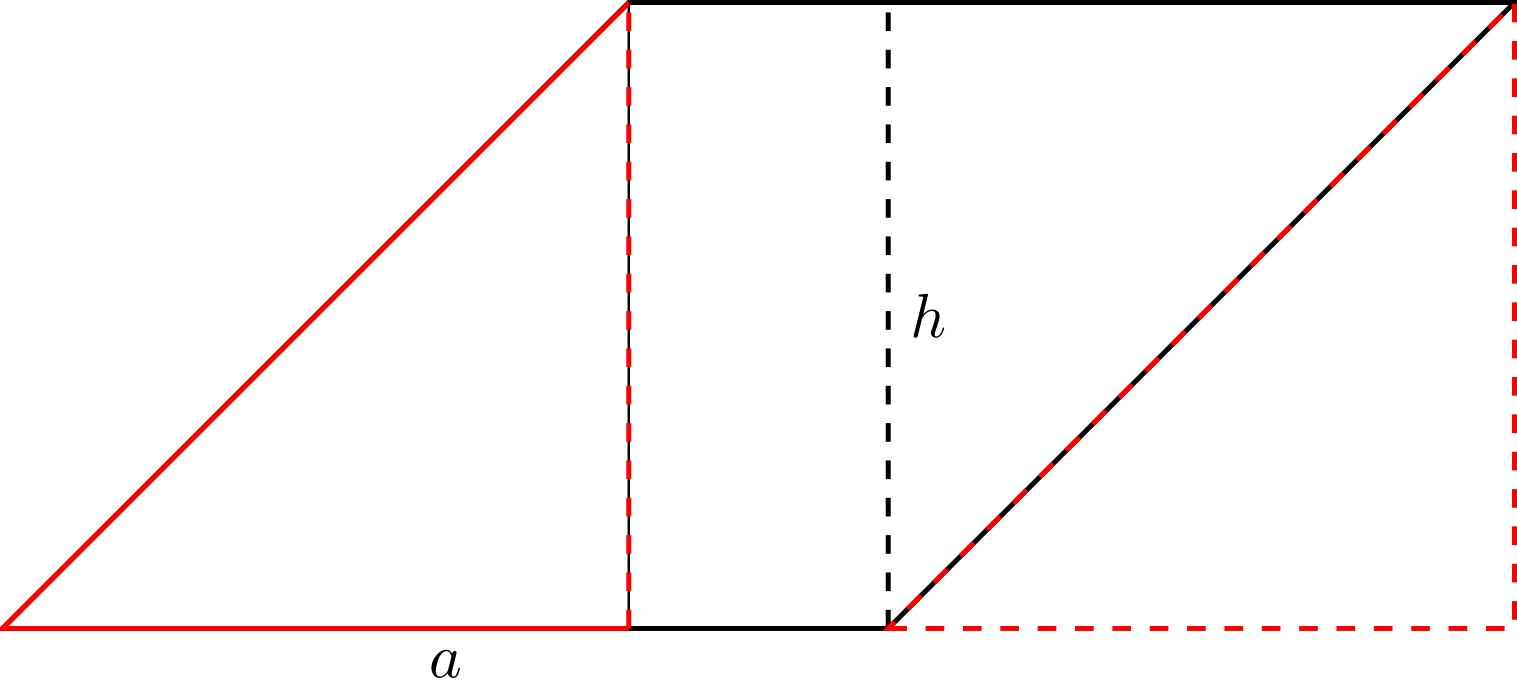
Und wie berechnet man die Fläche, wenn das Dreieck nicht rechtwinklig ist?
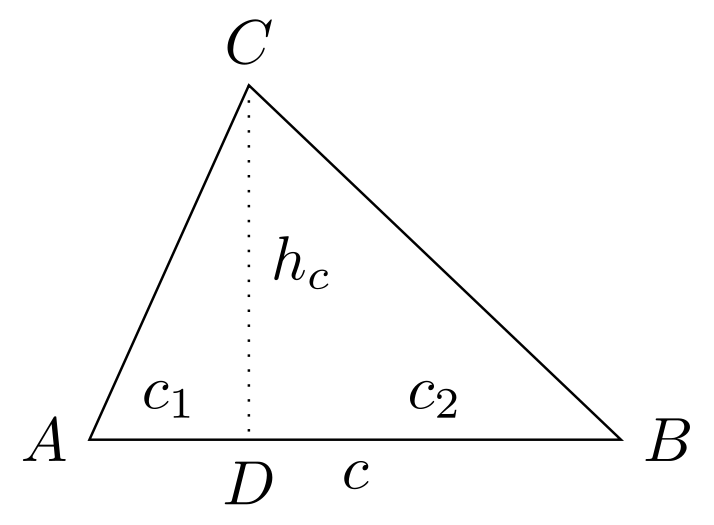
Aus jedem beliebigen Dreieck kann man zwei rechtwinklige Dreiecke gewinnen, indem man von einer Ecke aus eine Linie auf die gegenüberliegende Seite zieht, so dass sie diese senkrecht trifft. Diese Linie nennt man die Höhe eines Dreiecks auf die bestimmte Seite , wobei der Index derjenigen Seite , oder entspricht, über der die Höhe bestimmt wird.
Je nachdem, ob die neue Linie innerhalb oder außerhalb des Dreiecks liegt, ergibt sich der Flächeninhalt des Dreiecks dann aus der Summe oder der Differenz der Flächeninhalte der beiden sich ergebenden rechtwinkligen Dreiecke:
Links gilt also (wenn den Flächeninhalt des Dreiecks bezeichnet)
Rechts gilt
Somit kann der Flächeninhalt stets mittels einer Seitenlänge und der Länge der hierzu senkrechten Höhe berechnet werden.
|
|
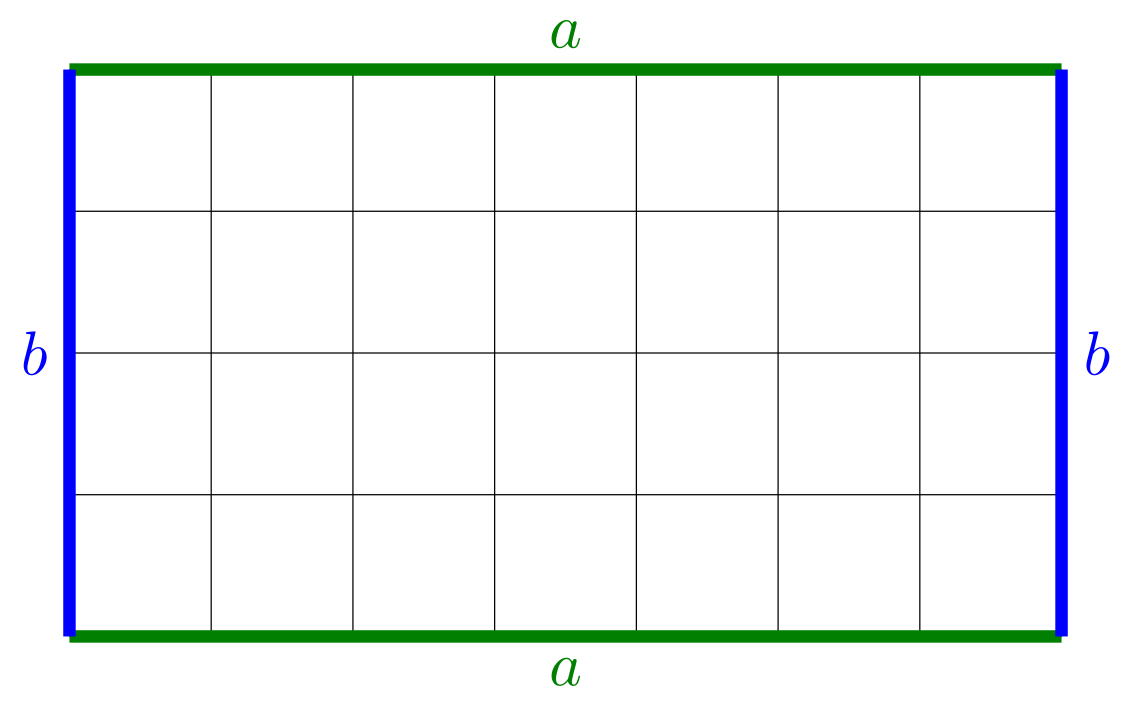
Fläche eines Rechtecks
5.4.10
Die Fläche eines Rechtecks mit den Längen und benachbarter Seiten ist
Die Fläche eines Rechtecks mit den Längen und benachbarter Seiten ist
|
|
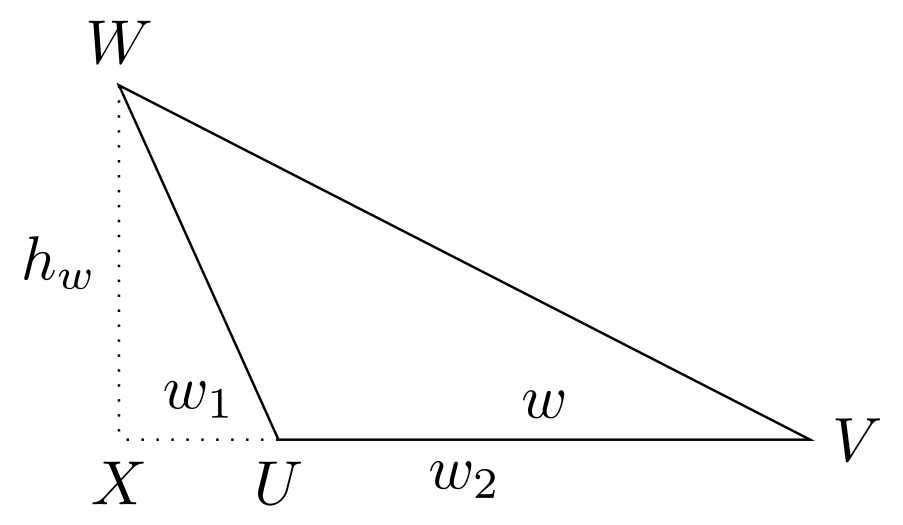
Und wie berechnet man die Fläche, wenn das Dreieck nicht rechtwinklig ist?
Aus jedem beliebigen Dreieck kann man zwei rechtwinklige Dreiecke gewinnen, indem man von einer Ecke aus eine Linie auf die gegenüberliegende Seite zieht, so dass sie diese senkrecht trifft. Diese Linie nennt man die Höhe eines Dreiecks auf die bestimmte Seite , wobei der Index derjenigen Seite , oder entspricht, über der die Höhe bestimmt wird.
Je nachdem, ob die neue Linie innerhalb oder außerhalb des Dreiecks liegt, ergibt sich der Flächeninhalt des Dreiecks dann aus der Summe oder der Differenz der Flächeninhalte der beiden sich ergebenden rechtwinkligen Dreiecke:
Links gilt also (wenn den Flächeninhalt des Dreiecks bezeichnet)
Rechts gilt
Somit kann der Flächeninhalt stets mittels einer Seitenlänge und der Länge der hierzu senkrechten Höhe berechnet werden.
Dreiecksfläche
5.4.11
Der Flächeninhalt eines Dreiecks berechnet sich aus der Hälfte des Produkts der Länge einer Seite mit der Länge der zugehörigen Höhe des Dreiecks:
Dabei ist die Höhe eines Dreiecks auf einer Seite die Strecke, die von dem der Seite gegenüberliegenden Punkt ausgeht und die Gerade, auf der die Seite liegt, im rechten Winkel trifft.
Der Flächeninhalt eines Dreiecks berechnet sich aus der Hälfte des Produkts der Länge einer Seite mit der Länge der zugehörigen Höhe des Dreiecks:
Dabei ist die Höhe eines Dreiecks auf einer Seite die Strecke, die von dem der Seite gegenüberliegenden Punkt ausgeht und die Gerade, auf der die Seite liegt, im rechten Winkel trifft.
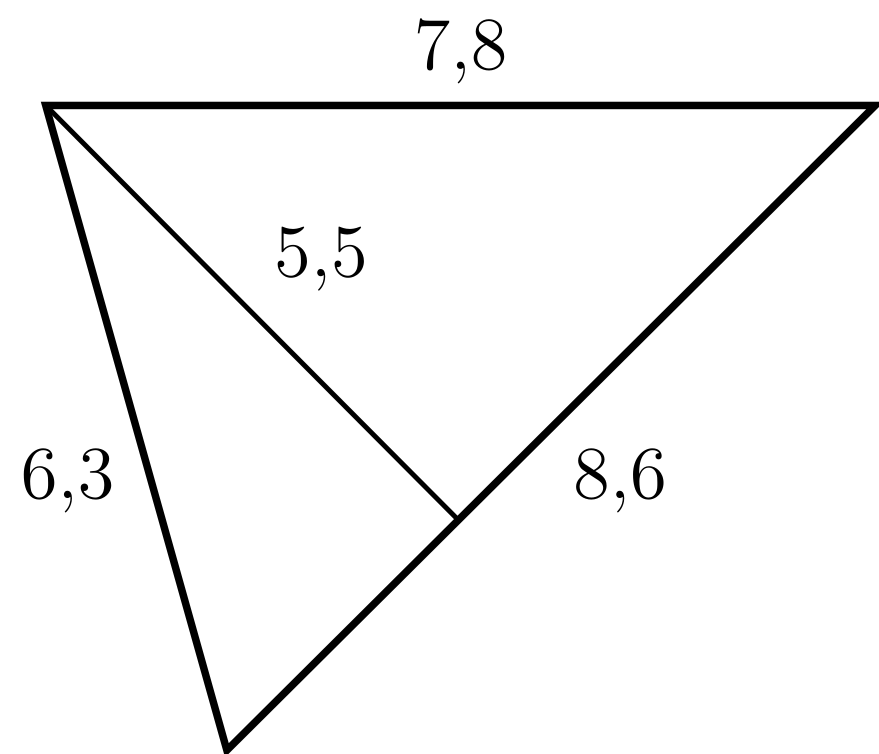
Beispiel
5.4.12
|
|
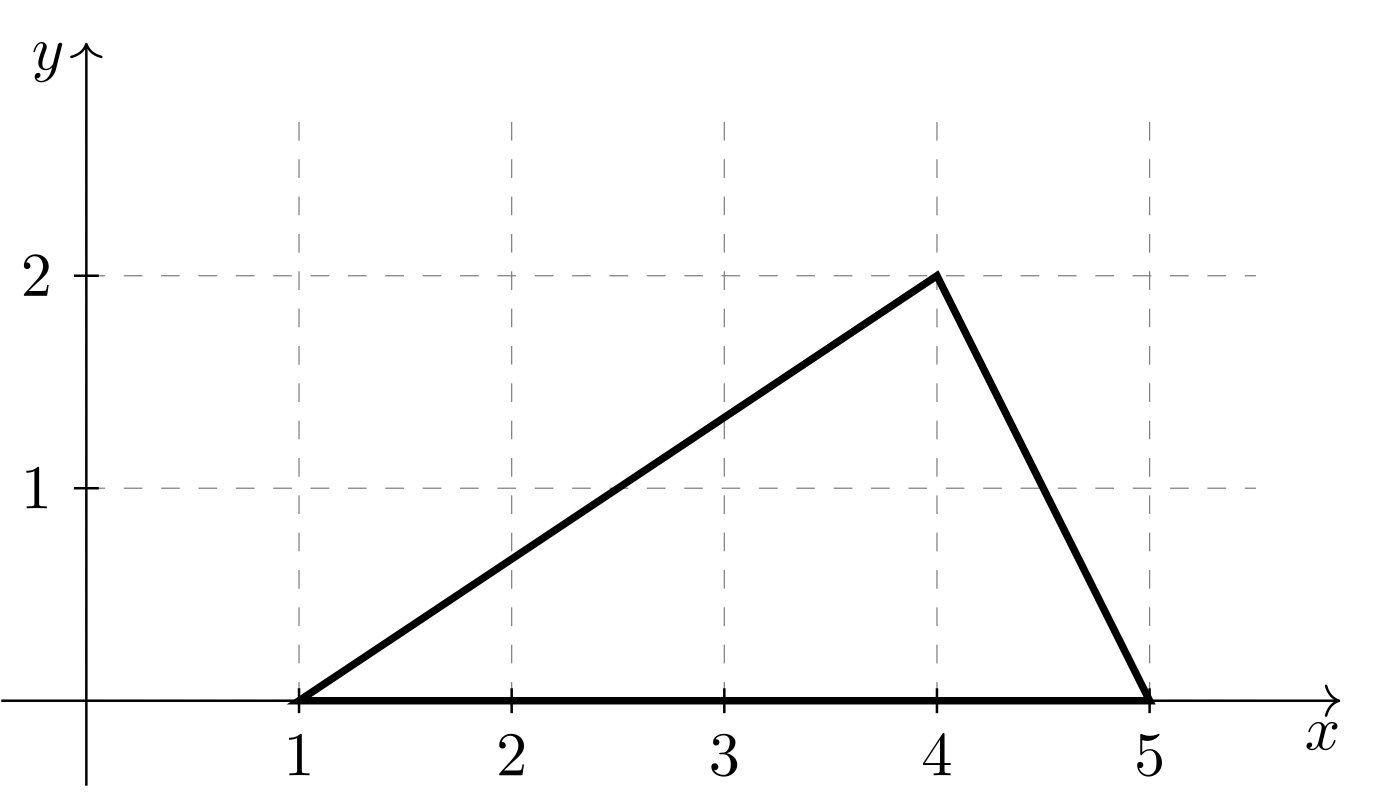
Mit der Formel für den Flächeninhalt von Dreiecken lassen sich auch Flächen von anderen Vielecken - auch Polygone genannt - bestimmen. Denn jedes Vieleck kann in Dreiecke unterteilt werden, indem man so lange Diagonalen einzeichnet, bis die Teilflächen Dreiecke sind. Die Summe der Flächeninhalte dieser Dreiecke ergibt den Flächeninhalt des Vielecks. Hier soll die Betrachtung jedoch auf einige einfache Formen beschränkt bleiben. Im folgenden Beispiel kann man das Vieleck in ein Dreieck und ein Rechteck zerlegen. Dadurch wird die Berechnung besonders einfach.
Beispiel
5.4.14
|
|
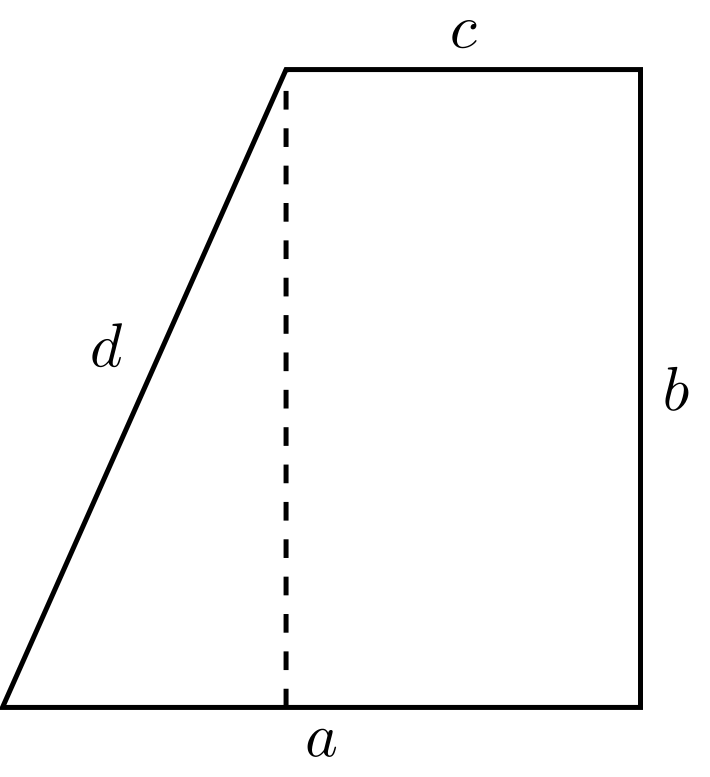
Aufgabe 5.4.15
|
|
Zum Schluss sollen noch Kreisflächen berechnet werden. In 5.2.6 wurde bereits die Kreiszahl vorgestellt, die das Verhältnis zwischen Umfang und Durchmessung eines Kreises beschreibt. Auch in der Formel für den Flächeninhalt von Kreisen kommt die Kreiszahl vor.
Flächeninhalt eines Kreises
5.4.16
Der Flächeninhalt eines Kreises mit dem Radius berechnet sich zu
Der Flächeninhalt eines Kreises mit dem Radius berechnet sich zu
Beispiel
5.4.17
Ein Kreis mit dem Radius habe einen Flächeninhalt von rund . Hieraus lässt sich die Kreiszahl näherungsweise berechnen: Aus folgt . Mit den angegebenen Werten ergibt sich der Näherungswert
Ein Kreis mit dem Radius habe einen Flächeninhalt von rund . Hieraus lässt sich die Kreiszahl näherungsweise berechnen: Aus folgt . Mit den angegebenen Werten ergibt sich der Näherungswert