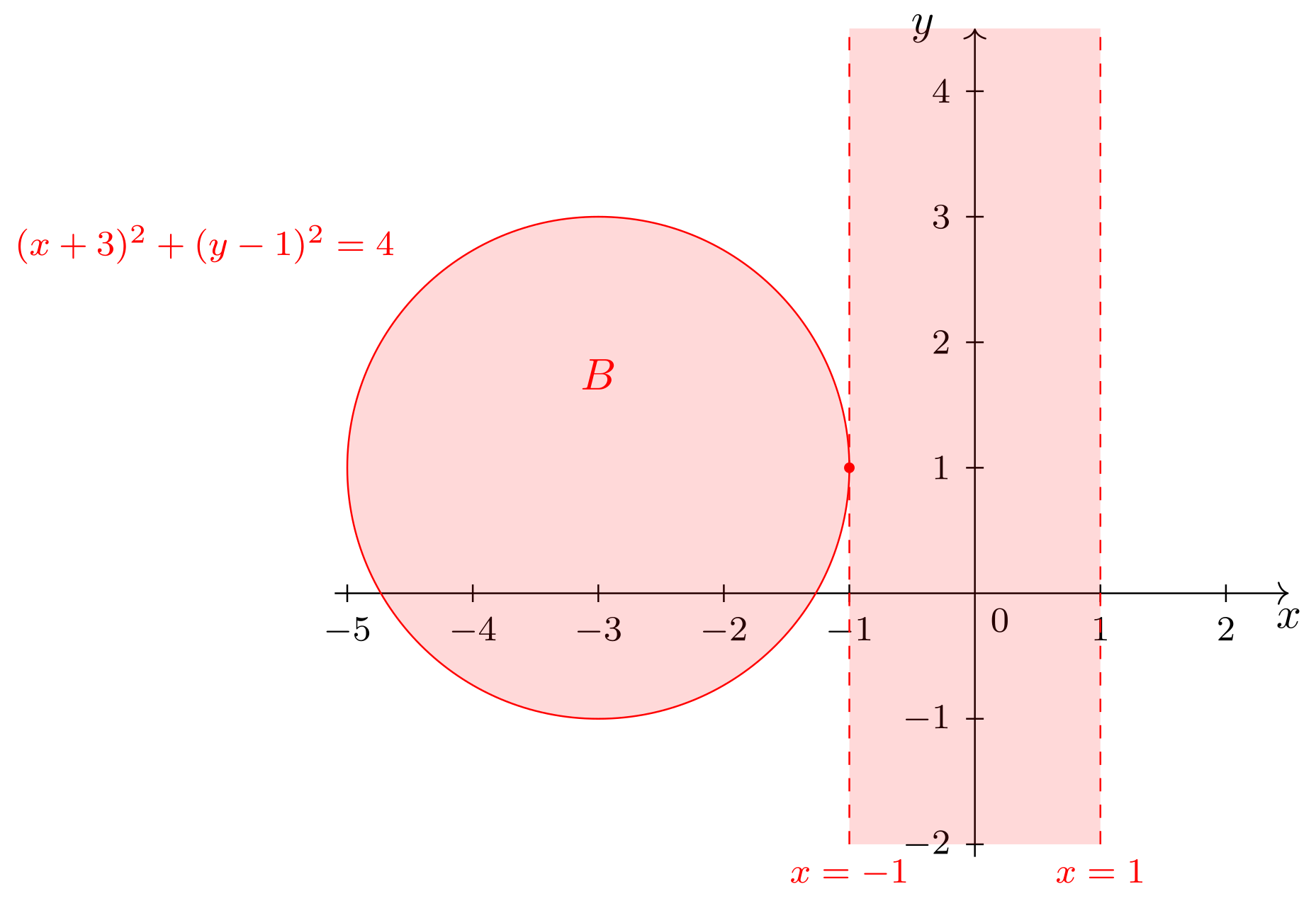
9.4.2 Von Geraden und Kreisen begrenzte Bereiche
Die folgende Infobox listet die möglichen entstehenden Bereiche auf, wenn man in einer Geradengleichung das Gleichheitszeichen durch ein Ungleichheitszeichen ersetzt.
Info
9.4.1
Ist eine Gerade in der Ebene (mit Steigung und Achsenabschnitt ) mittels einer Geradengleichung in Normalform bezüglich eines festen Koordinatensystems gegeben,
dann erhält man durch Ersetzen des Gleichheitszeichens durch ein Ungleichheitszeichen die folgenden Mengen, welche jeweils Bereiche in der Ebene beschreiben:
Ist eine Gerade in der Ebene (mit Steigung und Achsenabschnitt ) mittels einer Geradengleichung in Normalform bezüglich eines festen Koordinatensystems gegeben,
dann erhält man durch Ersetzen des Gleichheitszeichens durch ein Ungleichheitszeichen die folgenden Mengen, welche jeweils Bereiche in der Ebene beschreiben:
- „Bereich oberhalb der Geraden, ohne die Punkte auf der Geraden selbst“
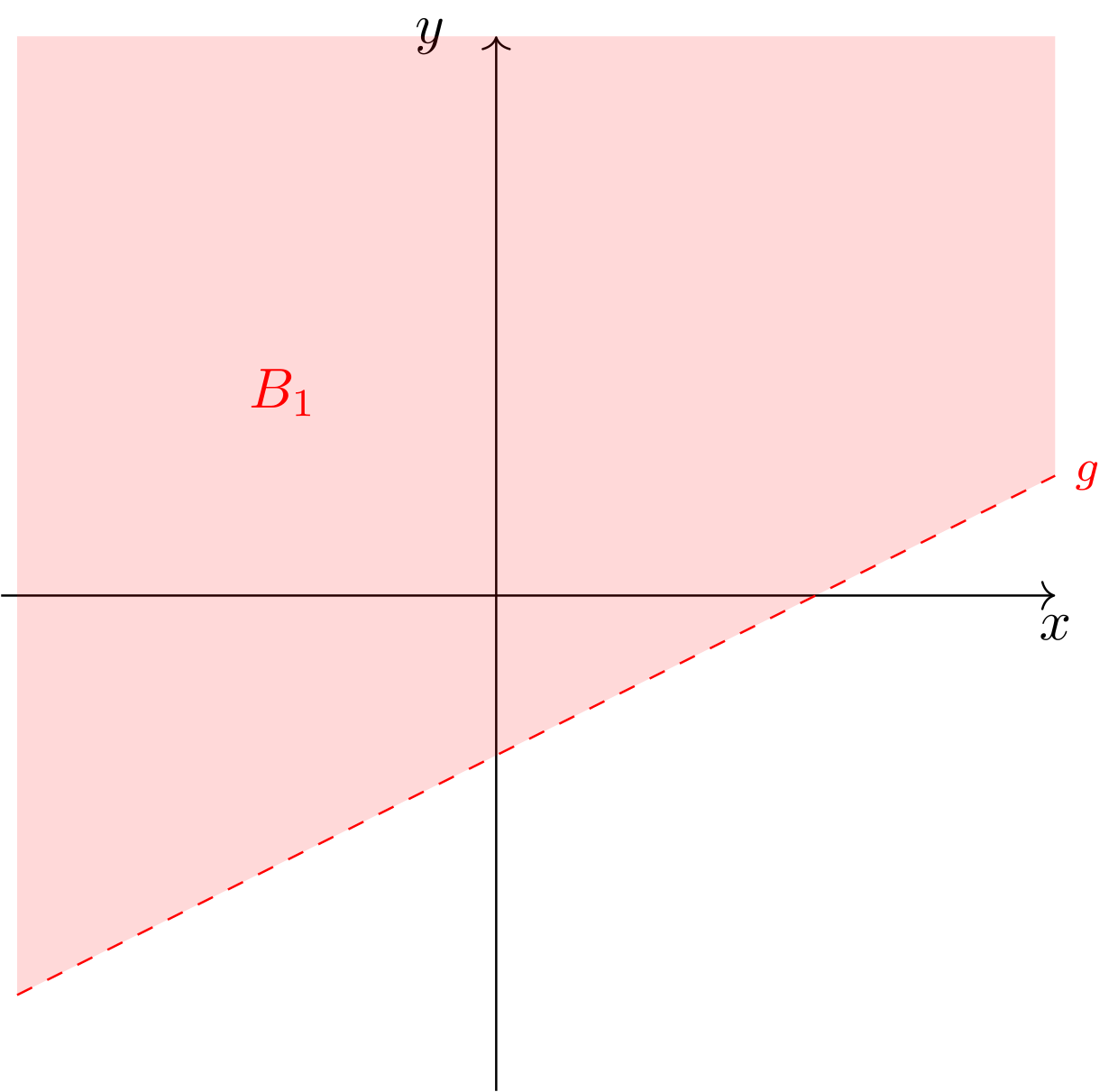 Abbildung 9.4.4: Skizze (C)
Abbildung 9.4.4: Skizze (C)
- „Bereich oberhalb der Geraden, inklusive der Punkte auf der Geraden“
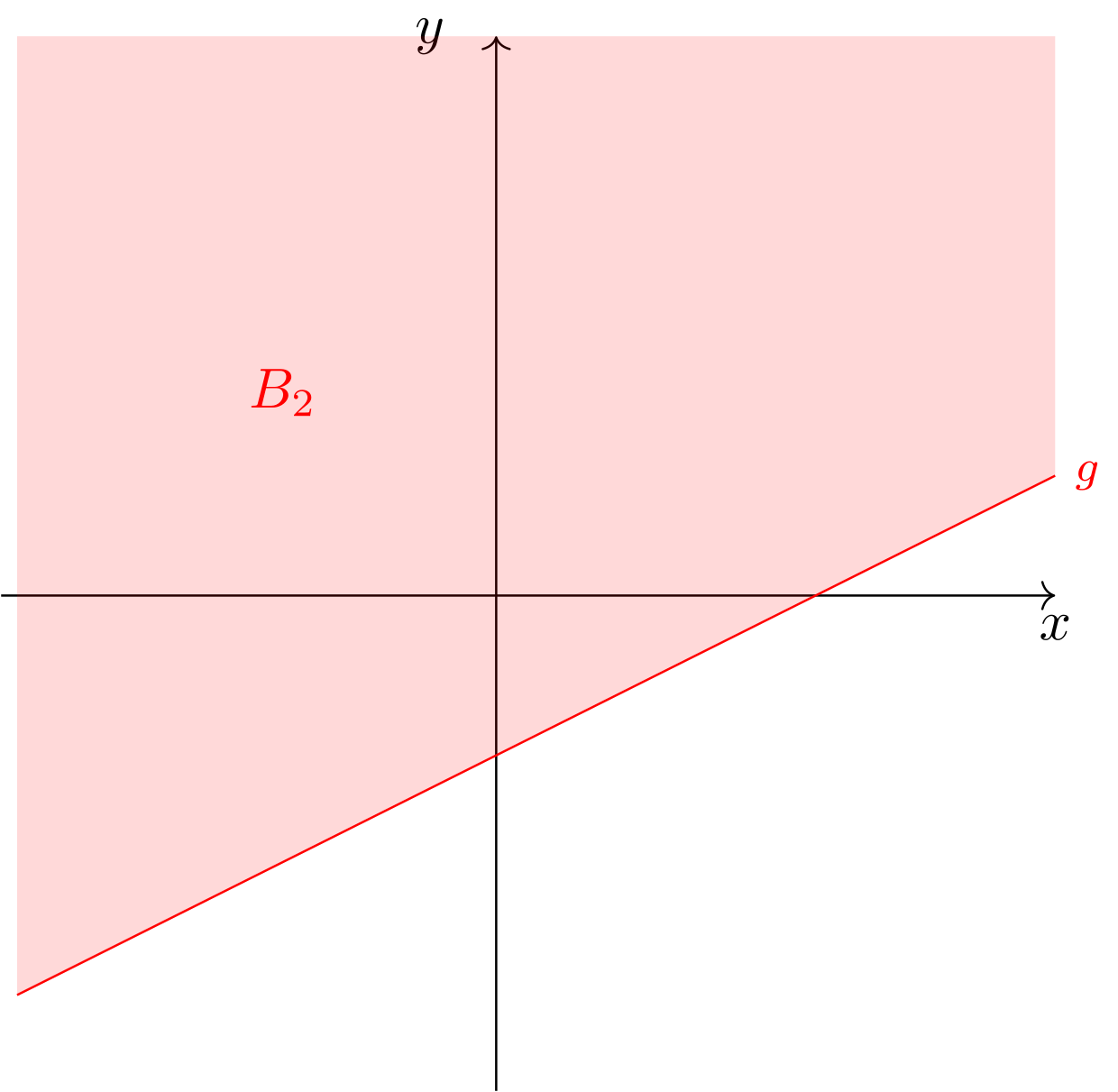 Abbildung 9.4.5: Skizze (C)
Abbildung 9.4.5: Skizze (C)
- „Bereich unterhalb der Geraden, ohne die Punkte auf der Geraden selbst“
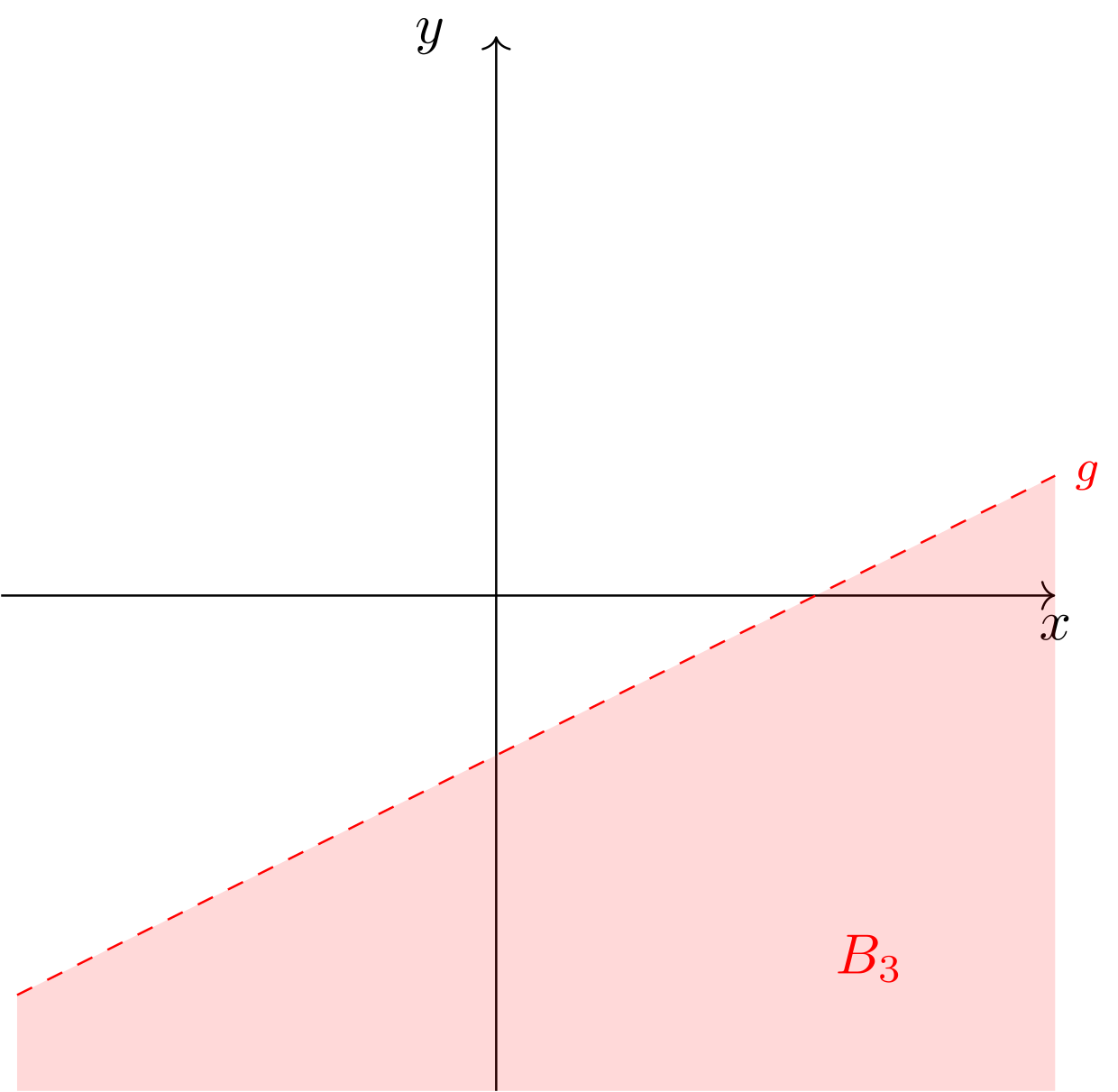 Abbildung 9.4.6: Skizze (C)
Abbildung 9.4.6: Skizze (C)
- „Bereich unterhalb der Geraden, inklusive Punkte auf der Geraden“
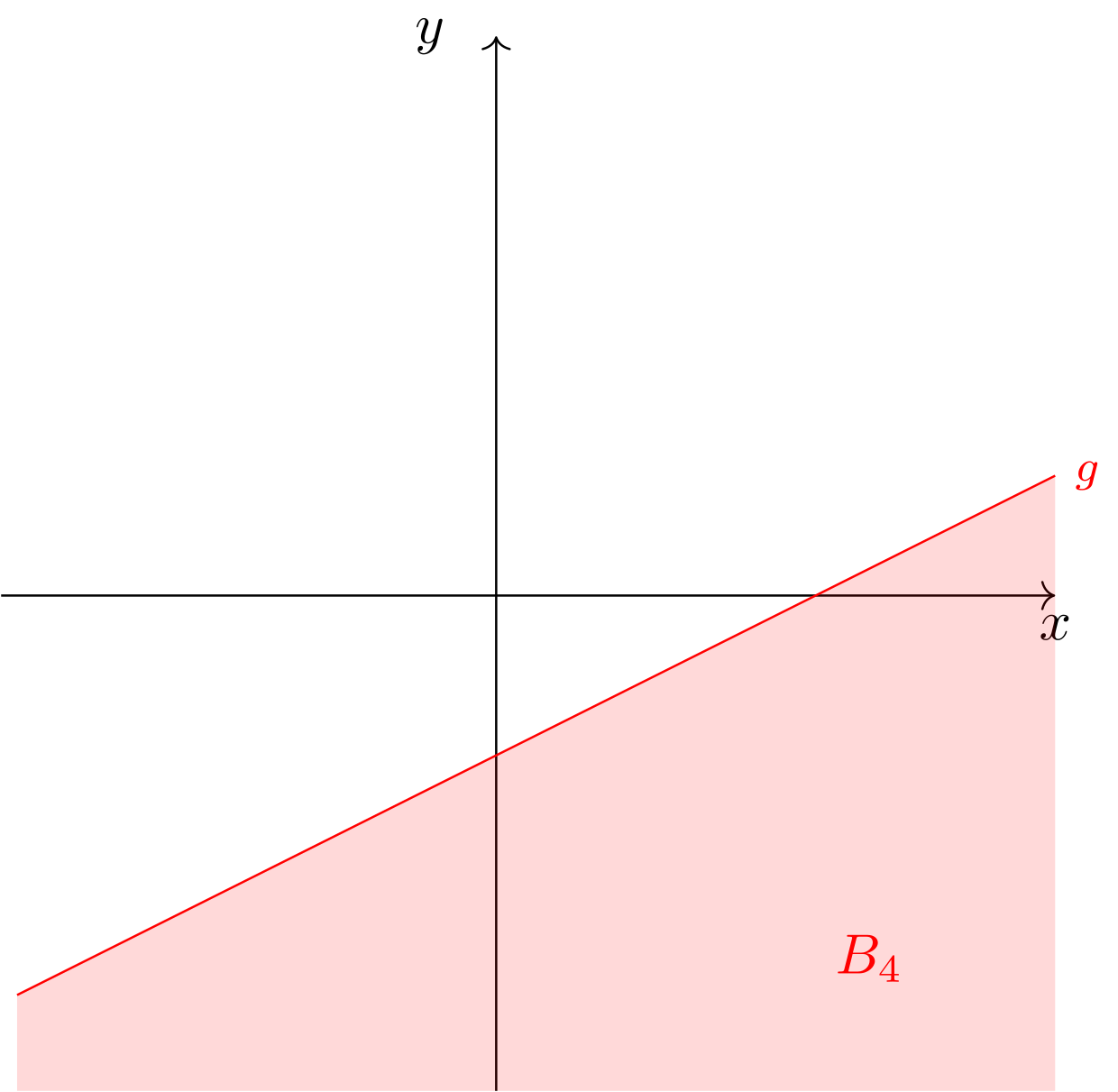 Abbildung 9.4.7: Skizze (C)
Abbildung 9.4.7: Skizze (C)
Für Geraden, die nicht auf Normalform gebracht werden können, funktioniert die Überlegung für die Bereiche völlig analog. Das folgende Beispiel zeigt zwei einfache Fälle.
Beispiel
9.4.2
Gegeben sind die beiden Geraden
und
Zu bestimmen und zu skizzieren sind die Mengen
sowie .
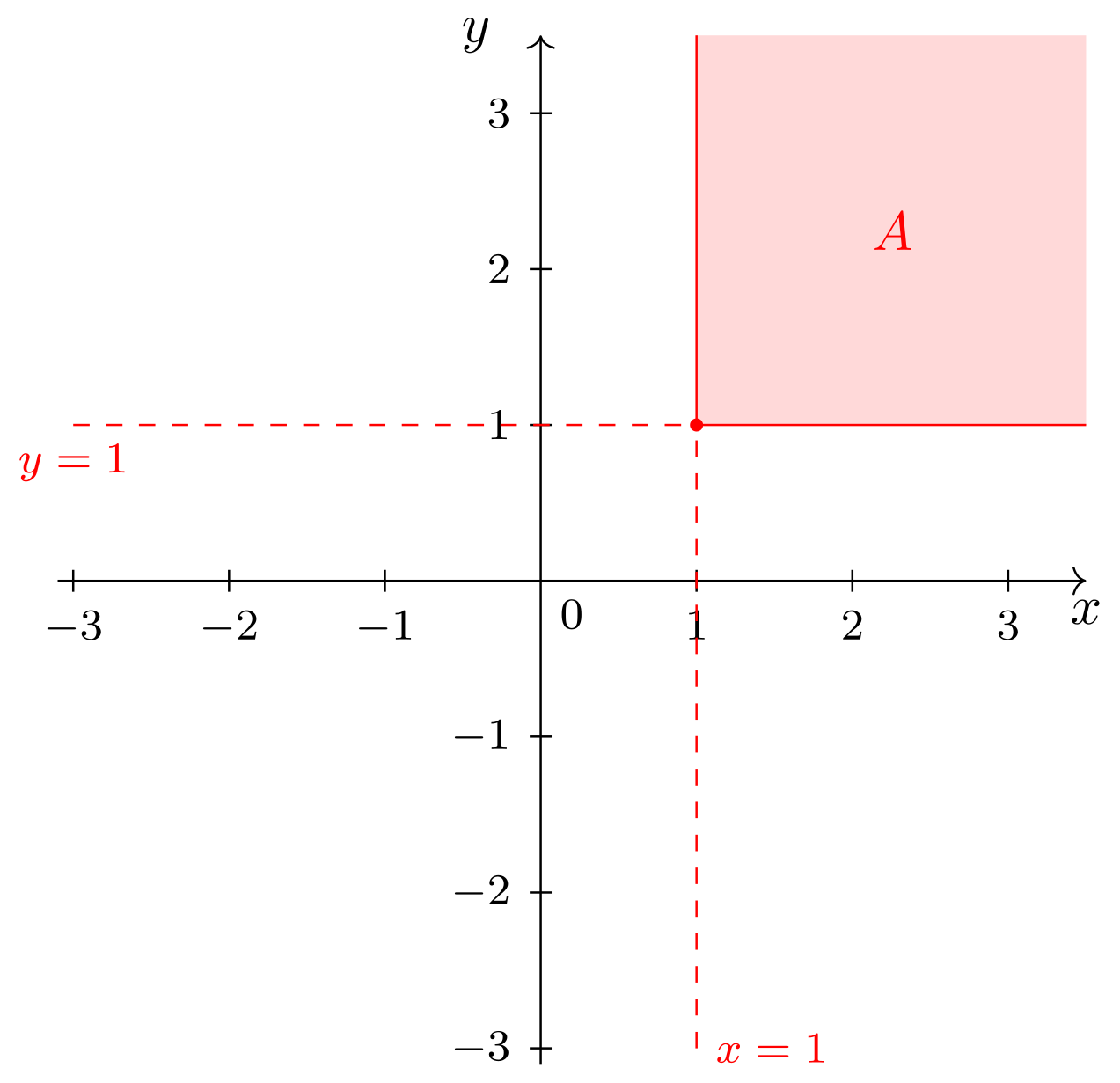
Zunächst gilt also
nach der Infobox oben und
da rechts der Geraden diejenigen Punkte liegen, deren -Koordinaten größer als sind. Die Schnittmenge sind diejenigen Punkte, welche beide Bedingungen erfüllen:
Bilder hierzu:
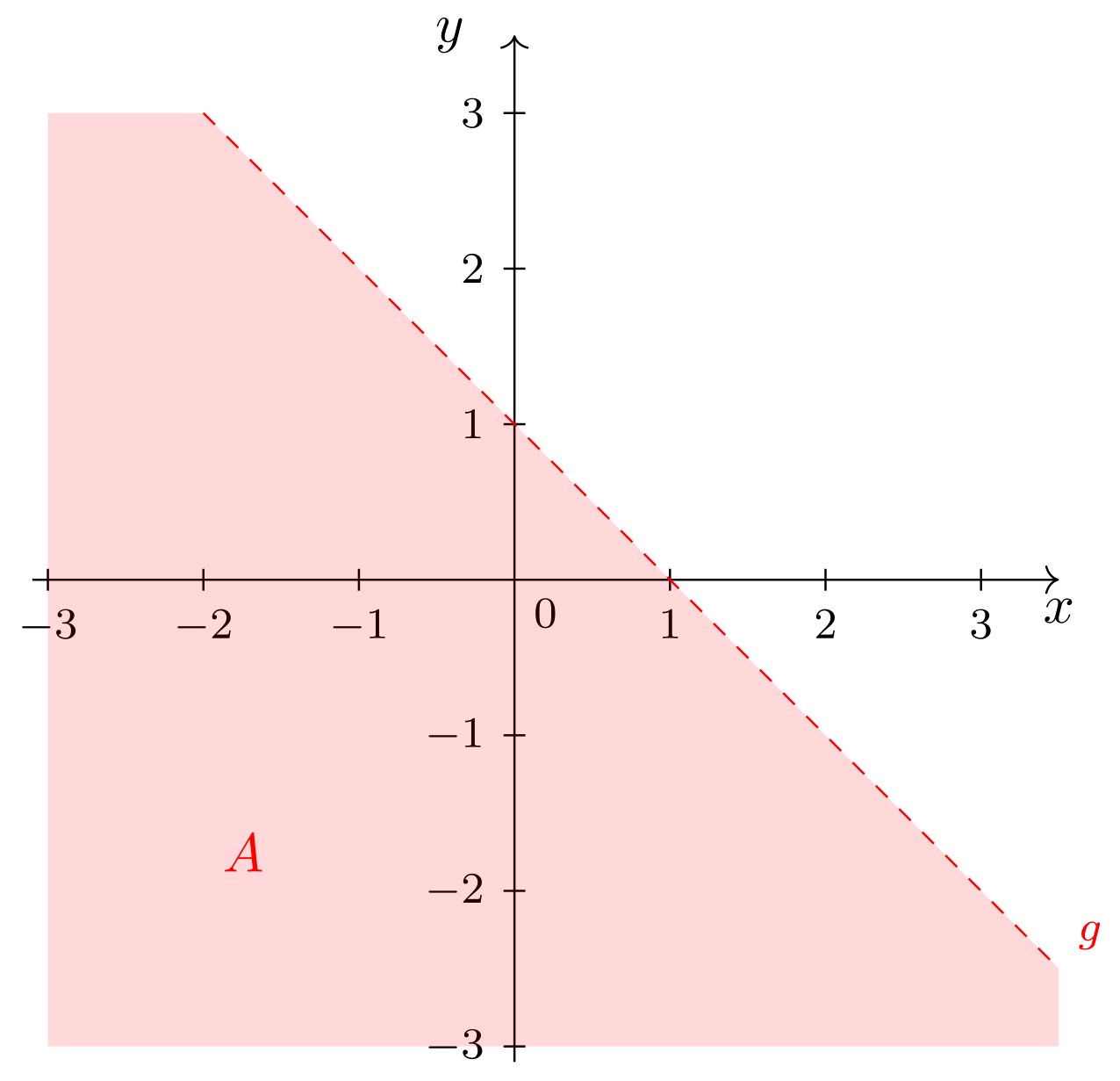
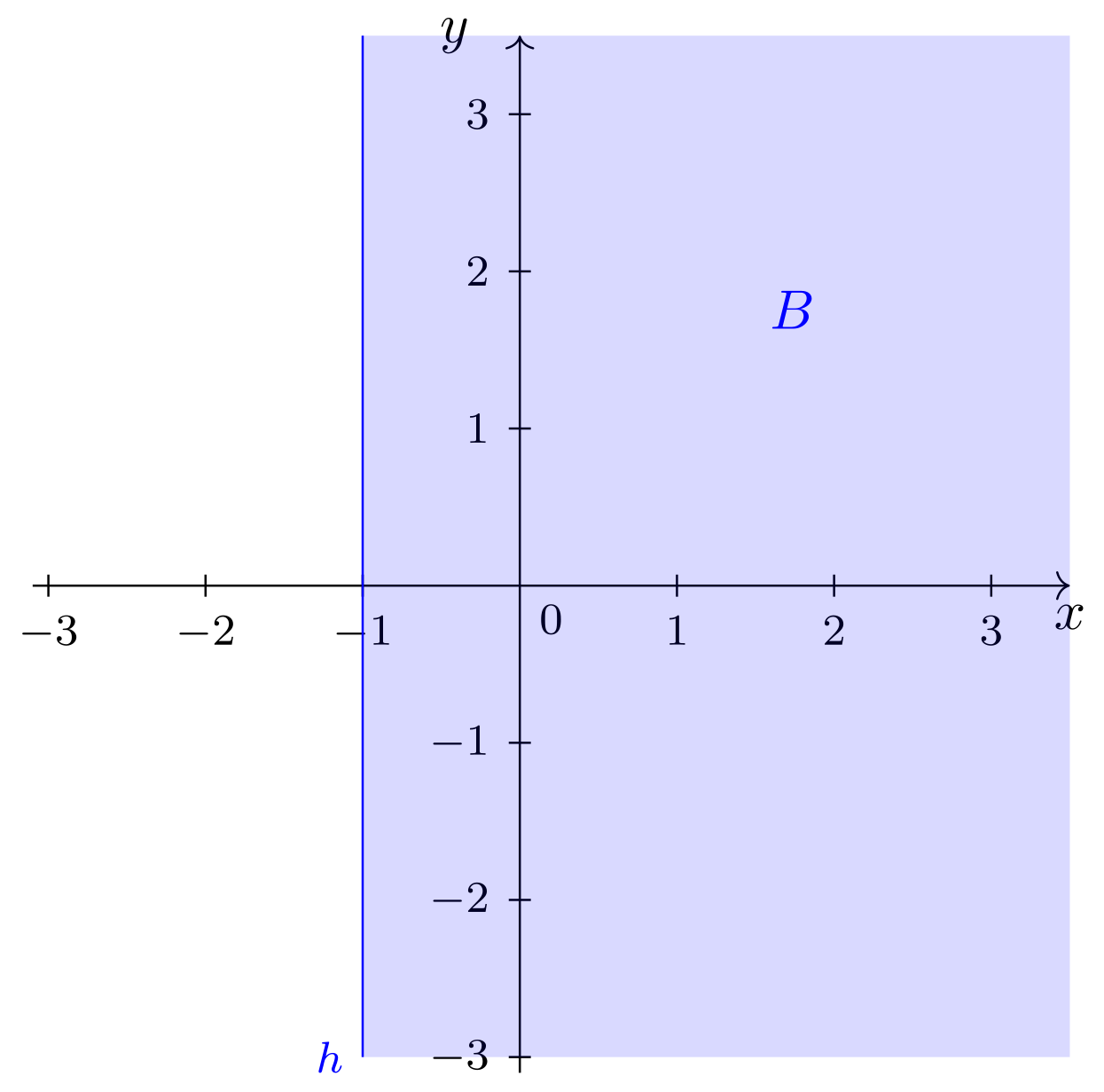
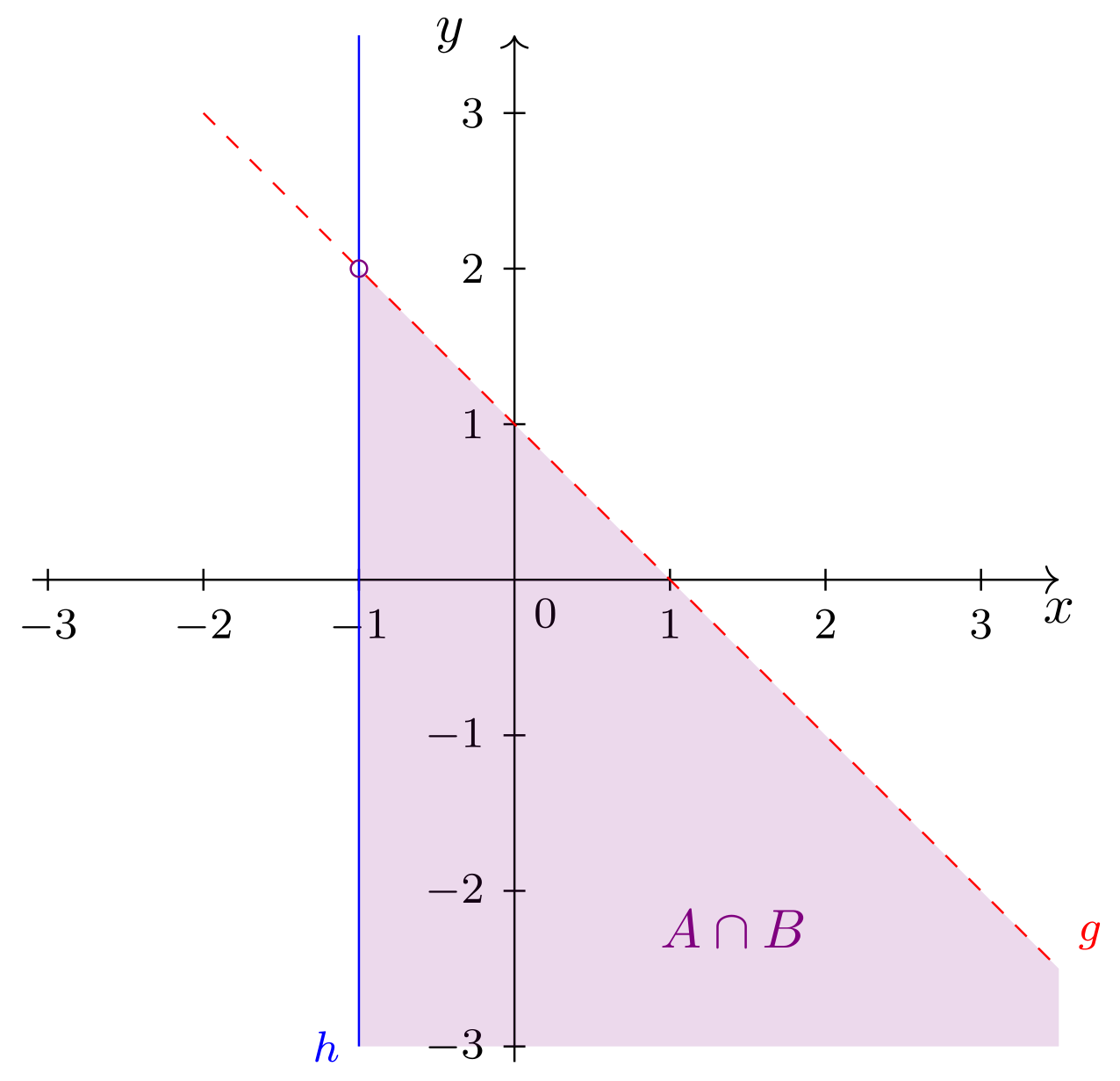
Der Schnittpunkt der beiden Geraden ist dabei kein Element von , da Punkte auf generell nicht zum Bereich gehören. Im Bild ist dies durch einen leeren Kringel angedeutet.
Gegeben sind die beiden Geraden
und
Zu bestimmen und zu skizzieren sind die Mengen
sowie .
Zunächst gilt also
nach der Infobox oben und
da rechts der Geraden diejenigen Punkte liegen, deren -Koordinaten größer als sind. Die Schnittmenge sind diejenigen Punkte, welche beide Bedingungen erfüllen:
Bilder hierzu:

Abbildung 9.4.8: Skizze (C)

Abbildung 9.4.9: Skizze (C)

Abbildung 9.4.10: Skizze (C)
Dieses Beispiel zeigt bereits Folgendes: Bereiche, welche durch nur eine Koordinatenungleichung gegeben sind, die aus einer Geradengleichung stammt, sind relativ einfach anzugeben. Es wird schwieriger, sobald Schnittmengen solcher Bereiche gesucht sind. Das folgende, etwas schwierigere, Beispiel zeigt, dass man nun auch noch Beträge mit ins Spiel bringen kann.
Beispiel
9.4.3
Es ist die Menge
in Worten zu beschreiben und zu skizzieren.
Wie üblich bei Beträgen (vgl. 2.2) ist eine Fallunterscheidung nötig:
Skizze hierzu:
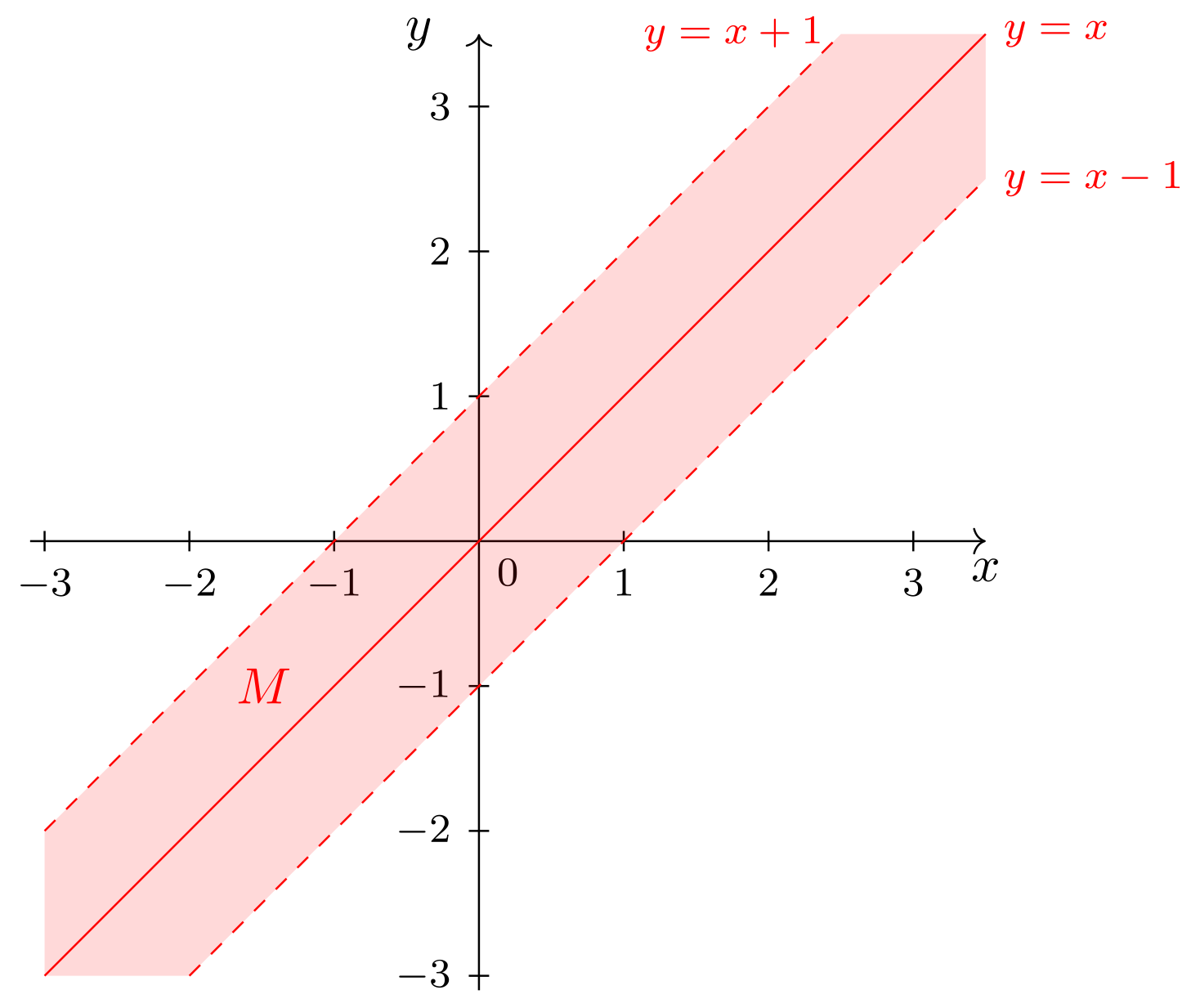
Es ist die Menge
in Worten zu beschreiben und zu skizzieren.
Wie üblich bei Beträgen (vgl. 2.2) ist eine Fallunterscheidung nötig:
-
Die Ungleichung lässt sich in diesem Fall auflösen zu
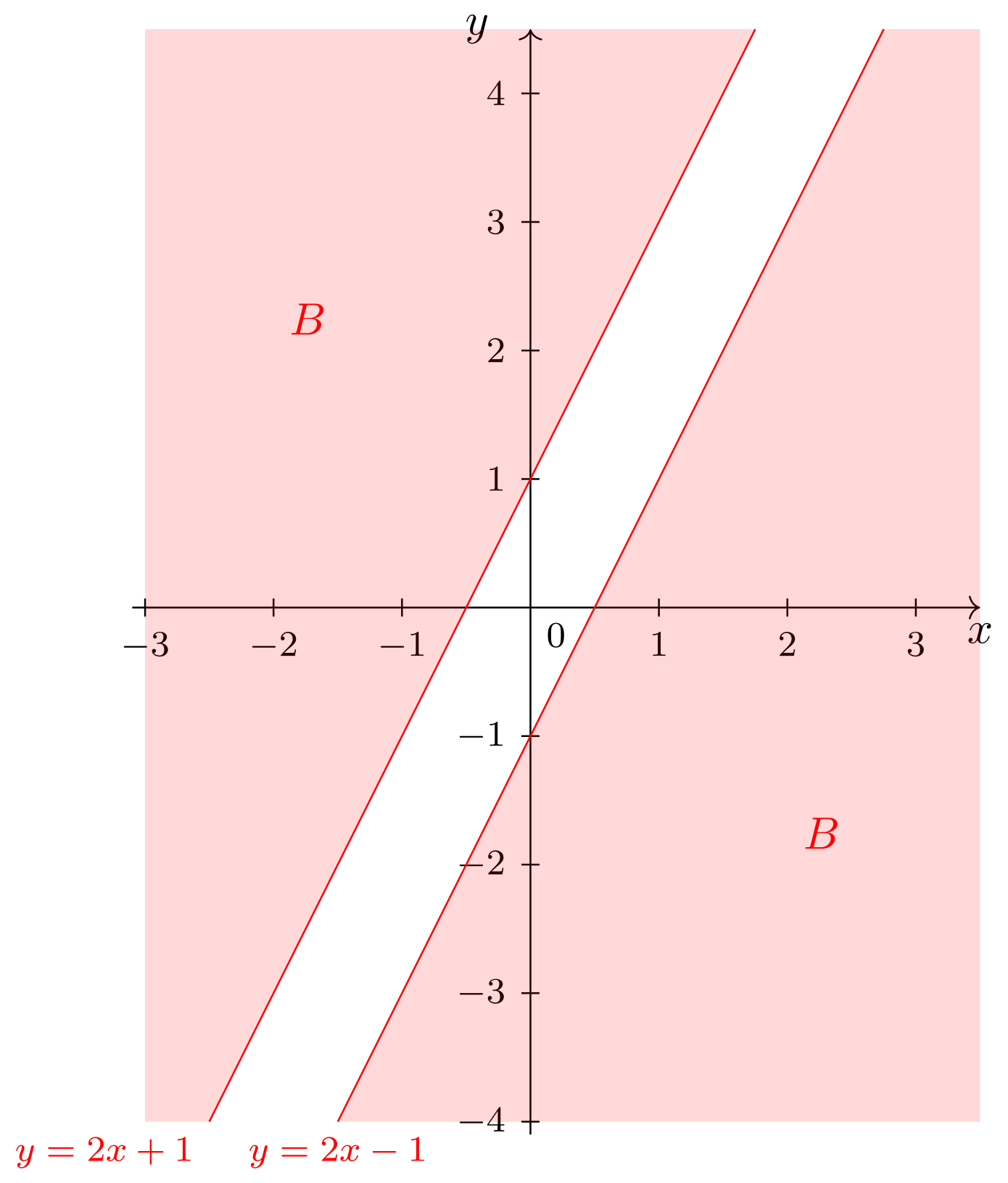
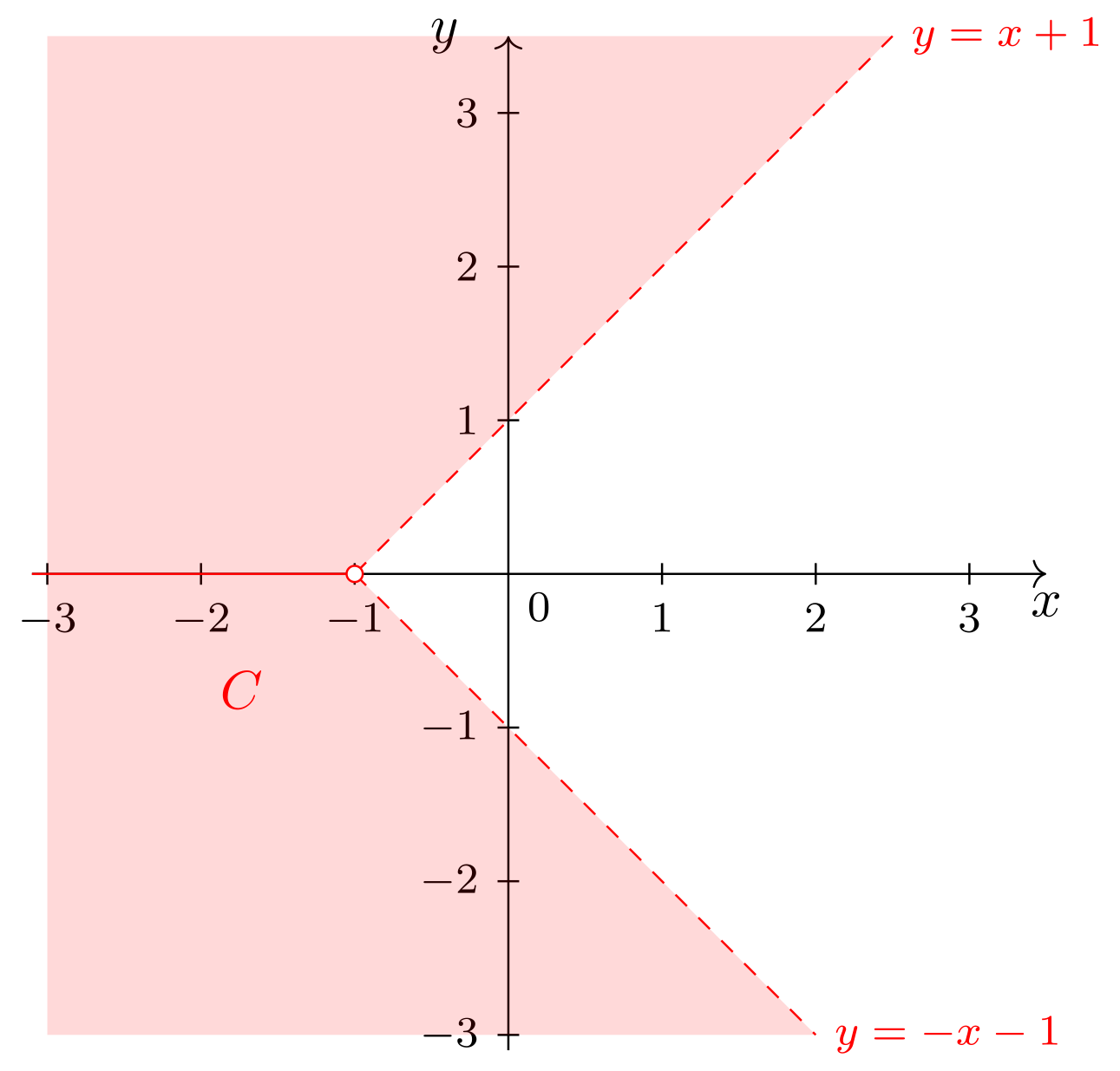
Somit liegen in diesem Fall alle in , die und erfüllen, also diejenigen Punkte, welche oberhalb der Geraden , aber unterhalb oder auf der Winkelhalbierenden liegen.
-
Die Ungleichung lässt sich in diesem Fall auflösen zu
Somit liegen in diesem Fall alle in , die und erfüllen, also diejenigen Punkte, welche unterhalb der Geraden , aber oberhalb der Winkelhalbierenden liegen.
Skizze hierzu:

Abbildung 9.4.11: Skizze (C)
Aufgabe 9.4.4
Skizzieren Sie jeweils die angegebenen Mengen:
Skizzieren Sie jeweils die angegebenen Mengen:
Die folgende Infobox fasst die möglichen Bereiche in der Ebene zusammen, die von einem Kreis begrenzt werden.
Info
9.4.5
Ist ein Kreis in der Ebene (mit Mittelpunkt und Radius ) mittels einer Kreisgleichung in Normalform bezüglich eines festen Koordinatensystems gegeben,
dann erhält man durch Ersetzen des Gleichheitszeichens durch ein Ungleichheitszeichen die folgenden Mengen, welche jeweils Bereiche in der Ebene beschreiben:
Ist ein Kreis in der Ebene (mit Mittelpunkt und Radius ) mittels einer Kreisgleichung in Normalform bezüglich eines festen Koordinatensystems gegeben,
dann erhält man durch Ersetzen des Gleichheitszeichens durch ein Ungleichheitszeichen die folgenden Mengen, welche jeweils Bereiche in der Ebene beschreiben:
- „Bereich innerhalb des Kreises, ohne die Punkte auf dem Kreis selbst“
 Abbildung 9.4.15: Skizze (C)
Abbildung 9.4.15: Skizze (C)
- „Bereich innerhalb des Kreises, inklusive der Punkte auf dem Kreis“
 Abbildung 9.4.16: Skizze (C)
Abbildung 9.4.16: Skizze (C)
- „Bereich außerhalb des Kreises, ohne die Punkte auf dem Kreis selbst“
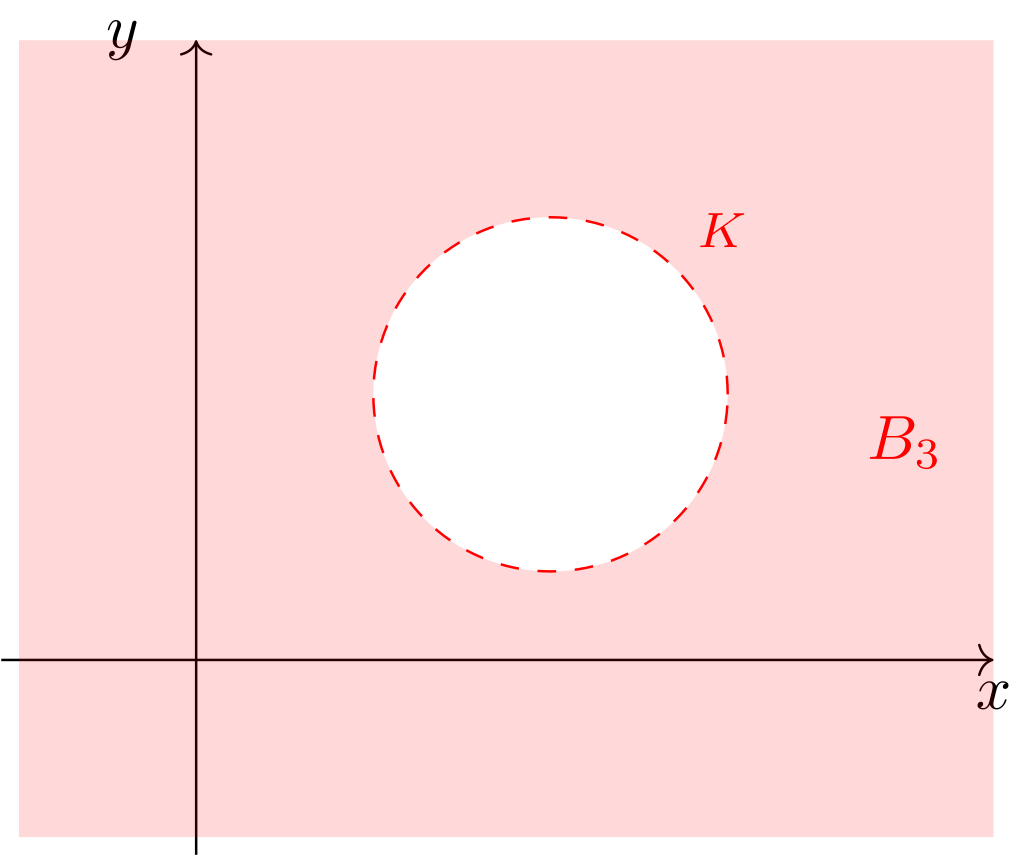 Abbildung 9.4.17: Skizze (C)
Abbildung 9.4.17: Skizze (C)
- „Bereich außerhalb des Kreises, inklusive der Punkte auf dem Kreis“
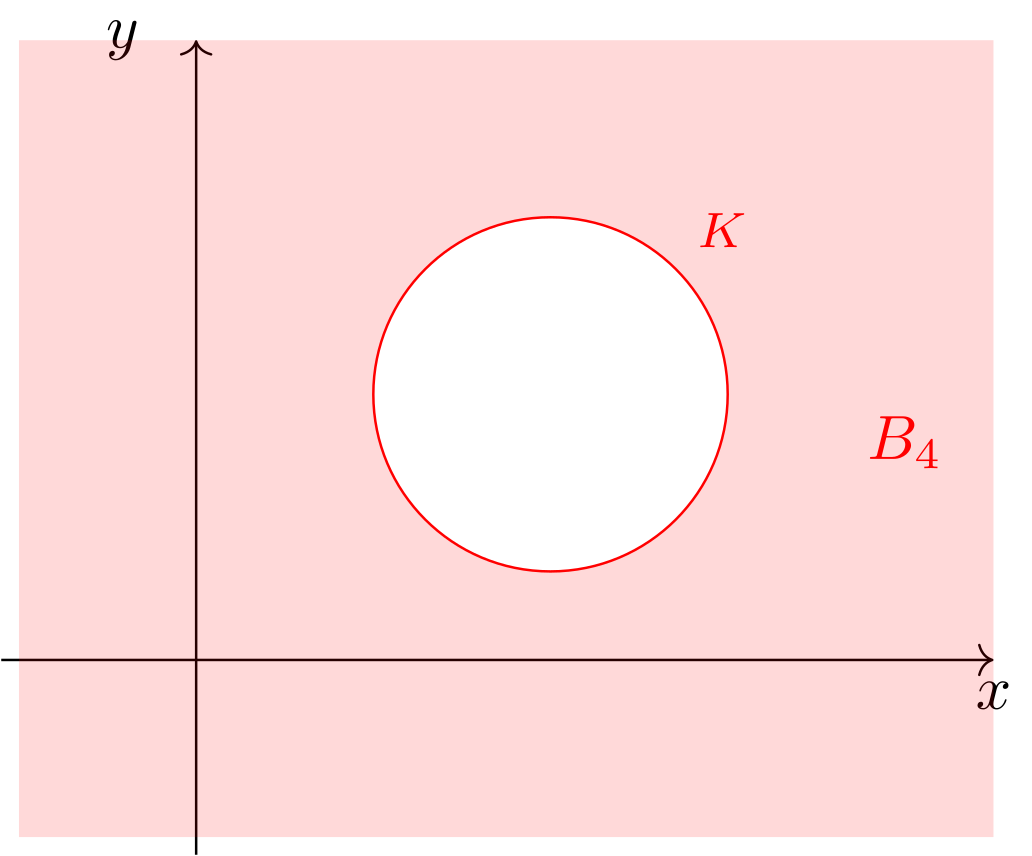 Abbildung 9.4.18: Skizze (C)
Abbildung 9.4.18: Skizze (C)
Das folgende Beispiel zeigt einige einfache Fälle von Bereichen, die von Kreisen begrenzt werden, sowie auch einige kompliziertere Fälle, die entstehen, wenn man mehrere Bereiche miteinander oder mit den Bereichen, welche von Geraden begrenzt werden, kombiniert.
Beispiel
9.4.6
Gegeben sind die Kreise
und
sowie die Gerade
Gegeben sind die Kreise
und
sowie die Gerade
- Die Menge besteht aus allen Punkten innerhalb und auf dem Kreis :
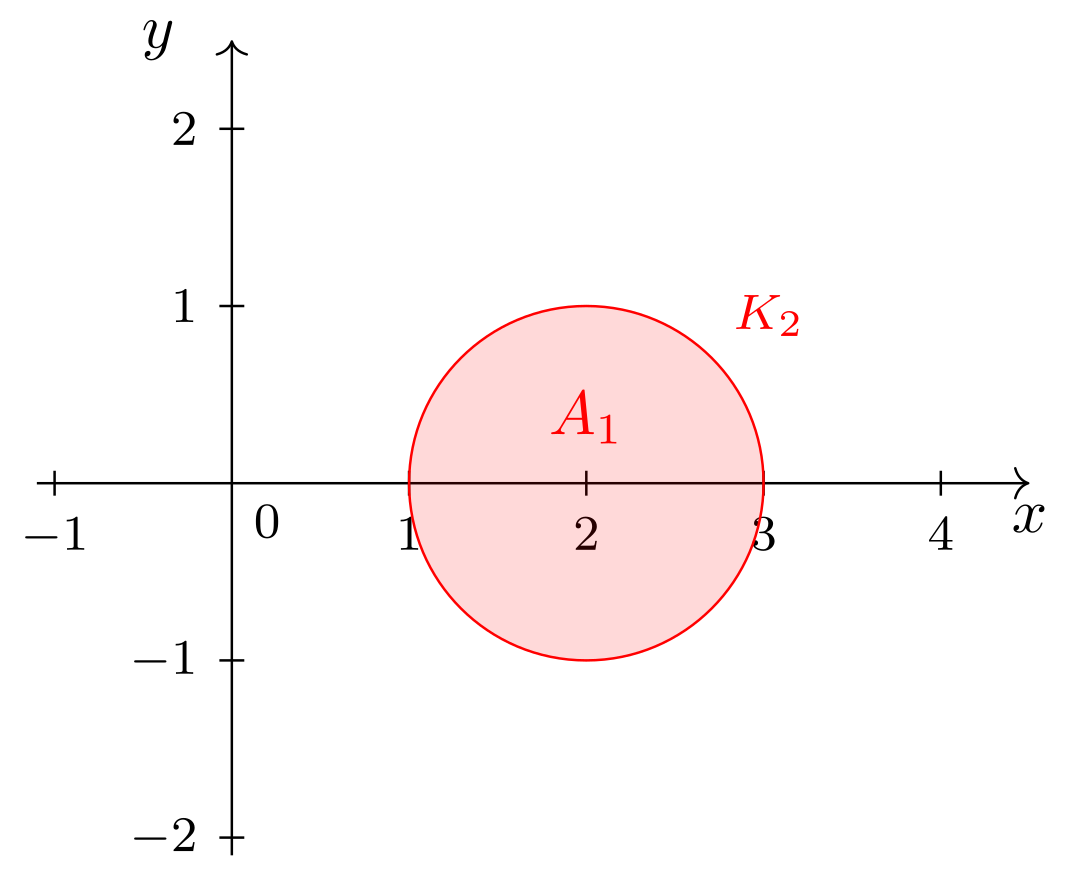 Abbildung 9.4.19: Skizze (C)
Abbildung 9.4.19: Skizze (C)
- Die Menge besteht aus allen Punkten, die sowohl innerhalb des Kreises als auch innerhalb des Kreises liegen, also im Schnitt der beiden Kreisscheiben, aber nicht auf den Kreisen selbst:
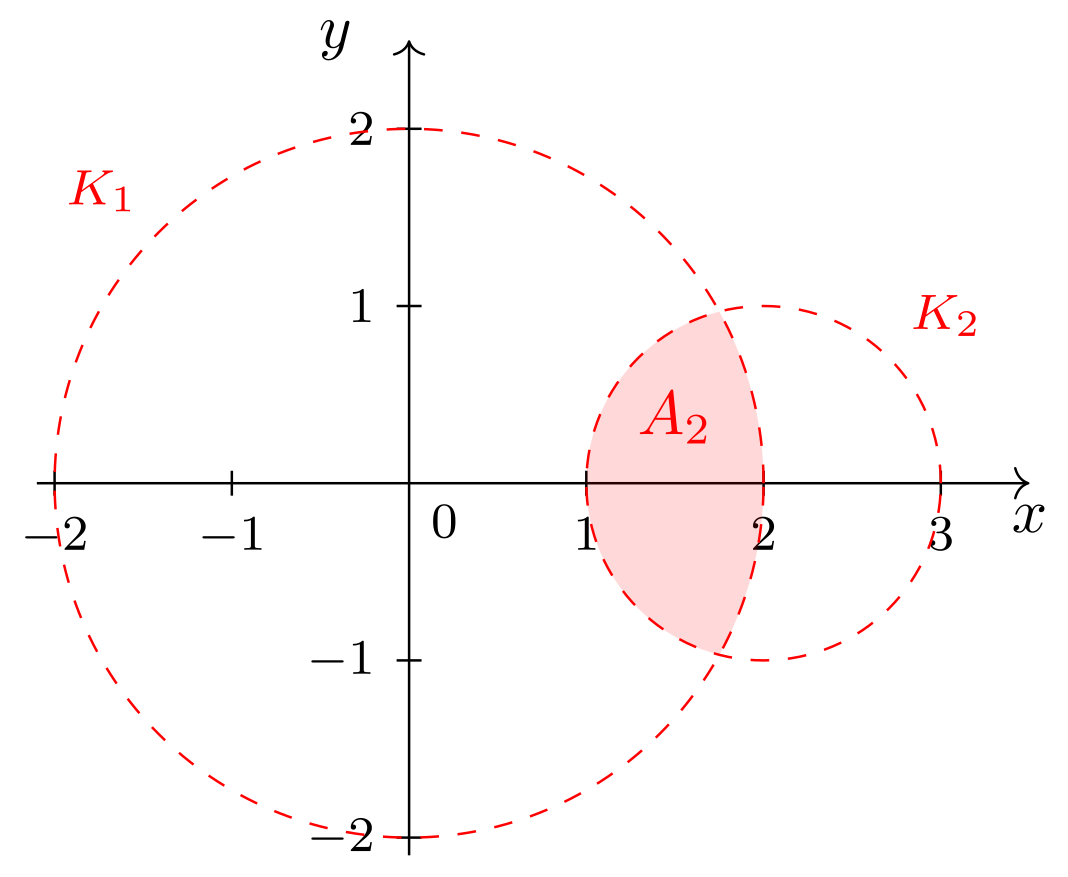 Abbildung 9.4.20: Skizze (C)
Abbildung 9.4.20: Skizze (C)
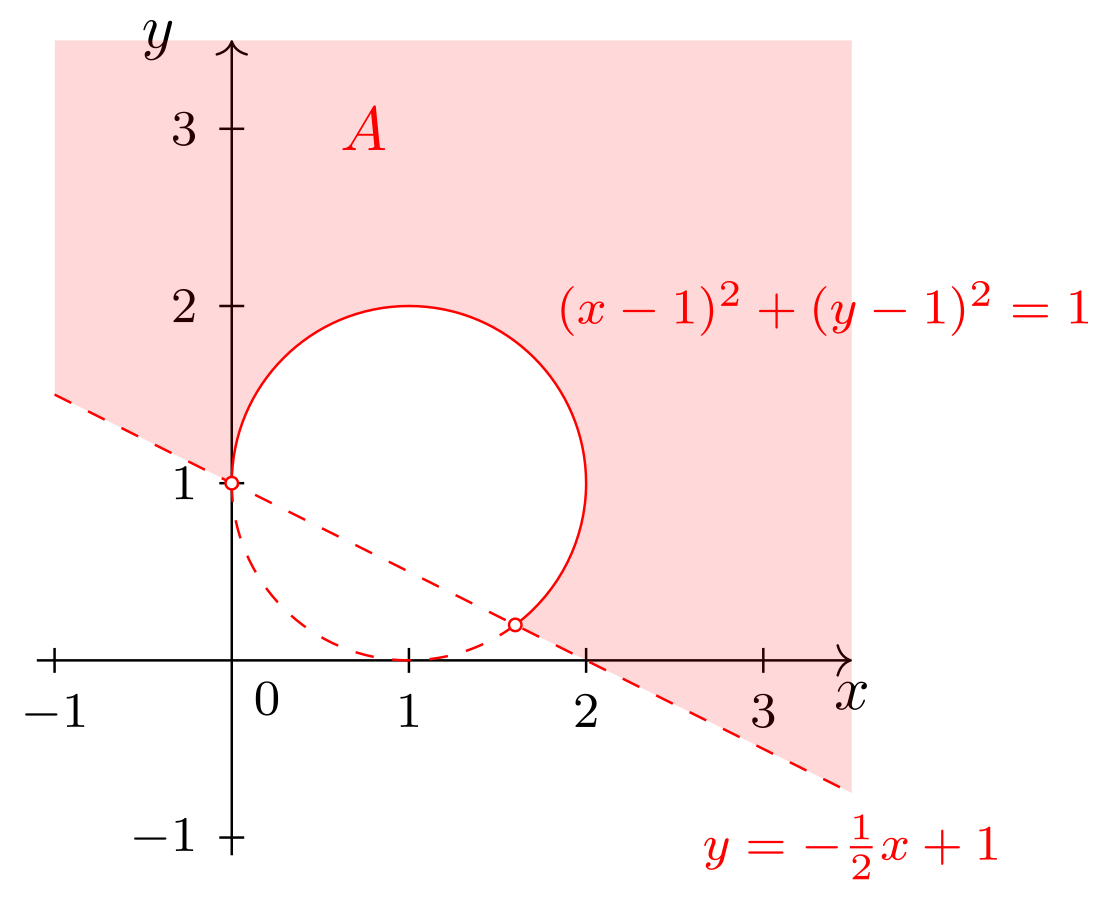
- Die Menge besteht aus allen Punkten, die sowohl innerhalb des Kreises - aber nicht auf dem Kreis - als auch auf oder oberhalb der Geraden liegen:
Die Schnittpunkte von Kreis und Gerade gehören nicht zu .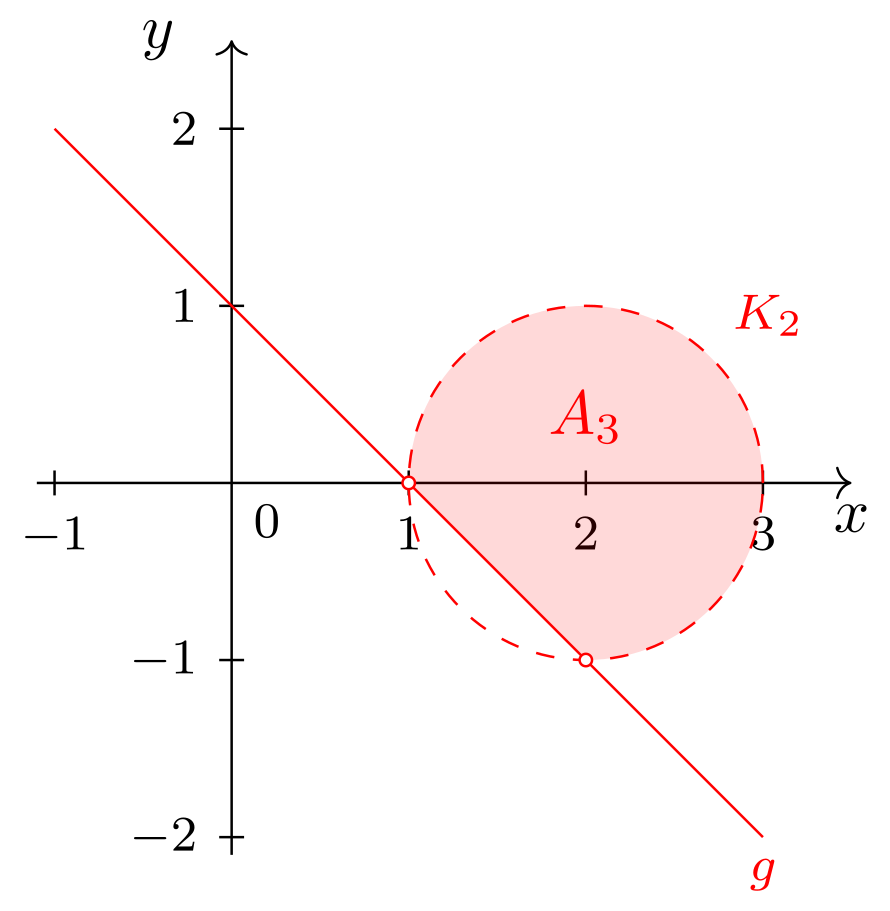 Abbildung 9.4.21: Skizze (C)
Abbildung 9.4.21: Skizze (C)
Aufgabe 9.4.7
Skizzieren Sie jeweils die angegebenen Mengen:
Skizzieren Sie jeweils die angegebenen Mengen: