7.1.2 Relative Änderungsrate einer Funktion
Es sollen eine Funktion , sowie eine Skizze des Graphen von (siehe unten) betrachtet werden. Das Ziel ist die Beschreibung der Änderungsrate dieser Funktion an einer beliebigen Stelle zwischen und . Dies wird auf den Begriff der Ableitung einer Funktion führen. Generell sollen möglichst einfache Rechenregeln Anwendung finden.
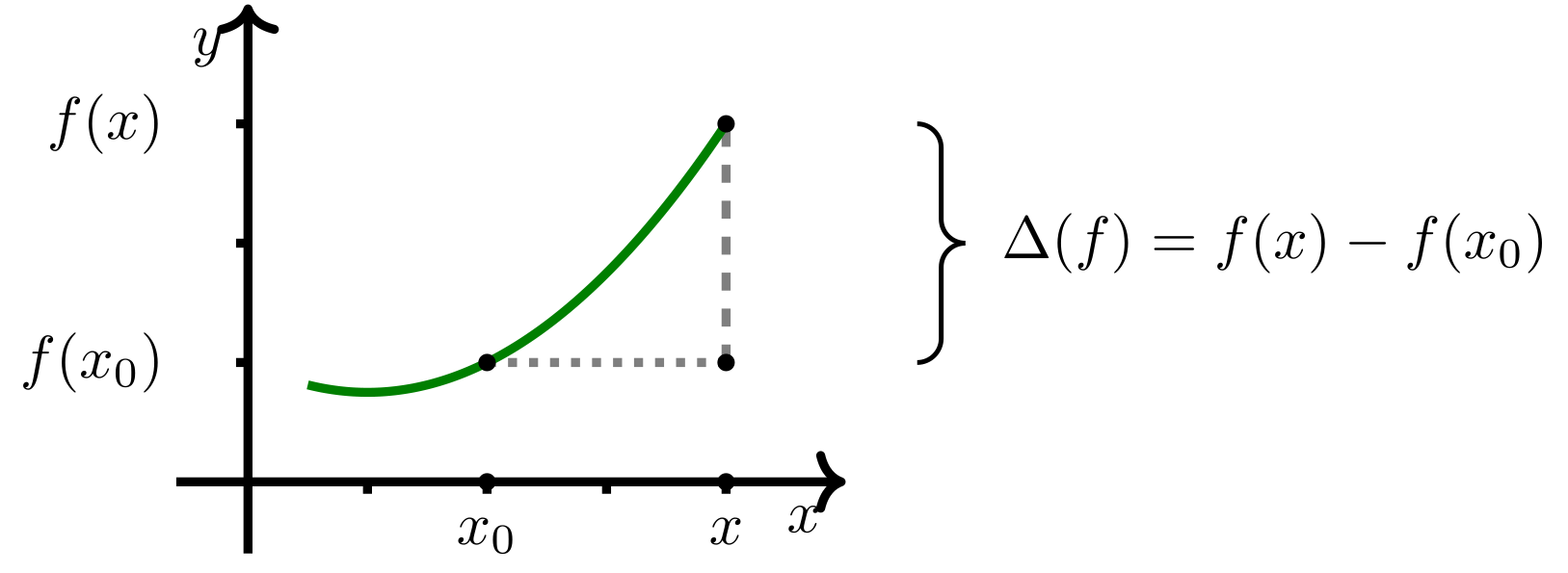
Abbildung 7.1.1: Skizze (C)
Werden und der entsprechende Funktionswert festgehalten und eine weitere beliebige, aber variable Stelle zwischen und sowie ihr Funktionswert ausgewählt, so lässt sich durch diese beiden Punkte, also durch und , eine Gerade legen, die durch ihre Steigung und ihren -Achsenabschnitt charakterisiert wird. Als Steigung dieser Geraden erhält man den sogenannten Differenzenquotienten
der beschreibt, wie sich die Funktionswerte von im Mittel zwischen und ändern. Damit ist eine mittlere Änderungsrate der Funktion im Intervall gefunden. Dieser Quotient wird auch als relative Änderung bezeichnet.
Strebt nun die variable Stelle gegen die Stelle , so stellt man fest, dass die Gerade, die den Graphen der Funktion in den Punkten und schneidet, immer mehr zu einer Tangente an den Graphen im Punkt wird. Auf diese Weise kann die Änderungsrate der Funktion - oder die Steigung des Graphen von - an der Stelle selbst bestimmt werden. Führt der geschilderte Prozess der Annäherung von an bildlich gesprochen auf eine eindeutige Tangente (mit einer eindeutigen Steigung, die insbesondere nicht unendlich sein darf), so spricht man in der Mathematik davon, dass der Grenzwert des Differenzenquotienten existiert. Beschrieben wird dieser Grenzwertprozess, dass gegen strebt, hier und im Folgenden mit dem Symbol
wobei abkürzend für Limes, das lateinische Wort für Grenze, steht. Existiert der Grenzwert des Differenzenquotienten, so bezeichnet
den Wert der Ableitung von in . Die Funktion ist dann an der Stelle ableitbar bzw. differenzierbar.
Beispiel
7.1.1
Für ist die relative Änderung an der Stelle gegeben durch
Bewegt sich nun auf zu, so resultiert der Grenzwert
Für den Wert der Ableitung von an der Stelle schreibt man .
Für ist die relative Änderung an der Stelle gegeben durch
Bewegt sich nun auf zu, so resultiert der Grenzwert
Für den Wert der Ableitung von an der Stelle schreibt man .
Aufgabe 7.1.2
Es sei mit und . In diesem Punkt beträgt die relative Änderung für ein reelles
 .
.
Rechnen Sie den Quotienten direkt aus, ohne bekannte Ableitungswerte und Regeln aus der Schule einzusetzen.
Bewegt sich auf zu, so erhält man die Steigung des Graphen von an der Stelle .
des Graphen von an der Stelle .
Es sei mit und . In diesem Punkt beträgt die relative Änderung für ein reelles
Rechnen Sie den Quotienten direkt aus, ohne bekannte Ableitungswerte und Regeln aus der Schule einzusetzen.
Bewegt sich auf zu, so erhält man die Steigung
Über die Formel für die relative Änderungsrate kann man die Ableitung nur sehr mühsam und auch nur für sehr einfache Funktionen ausrechnen. Typischerweise bestimmt man die Ableitung durch Anwenden von Rechenregeln und durch Einsetzen bekannter Ableitungswerte für die einzelnen Bausteine.


