8.2.5 Aufgaben
In der ersten Aufgabe wird die Idee zur Definition des Integrals aufgegriffen, mittels geeigneter Zerlegungen den Integralwert zu berechnen, wobei in der Aufgabe neben Rechtecken allgemeiner beispielsweise auch Dreiecksflächen verwendet werden.
Aufgabe 8.2.16
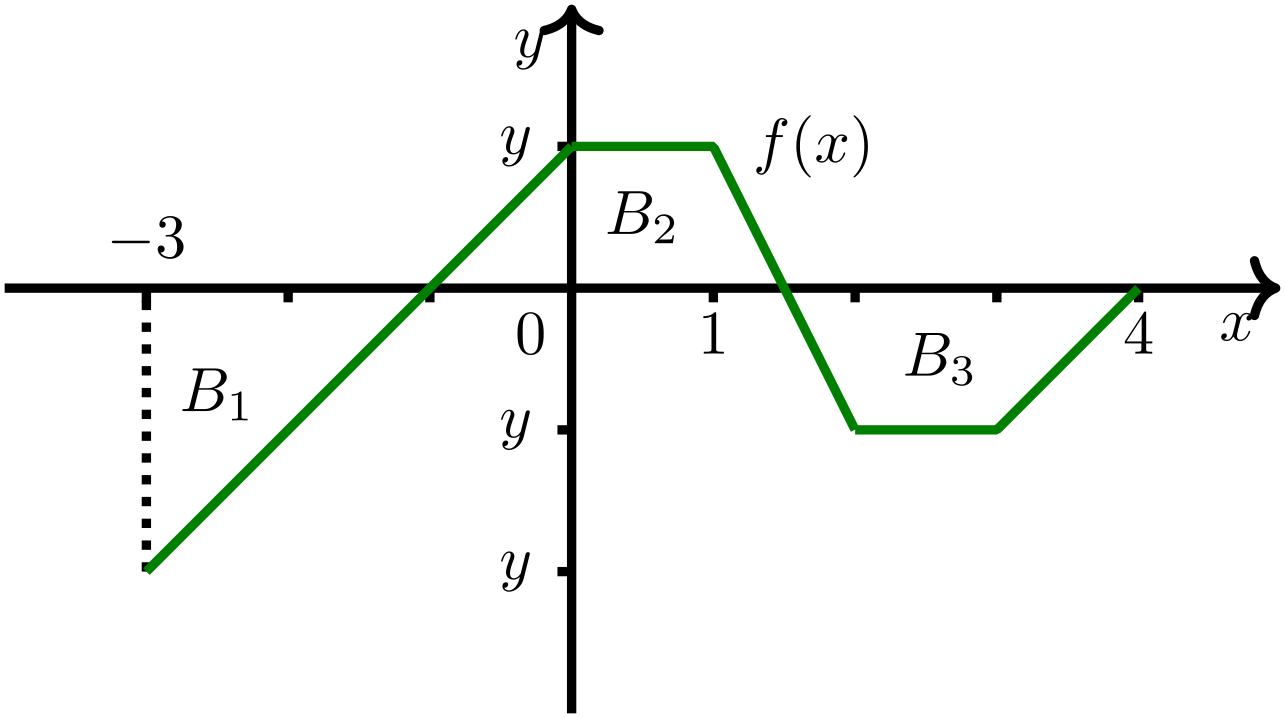
Berechnen Sie zu mit dem unten dargestellten Graphen das Integral mit Methoden aus der elementaren Geometrie, indem Sie die entsprechende Fläche „unter dem Graphen der Funktion“ in elementare geometrische Flächen wie Dreiecke oder Rechtecke zerlegen, die entweder oberhalb oder unterhalb der -Achse liegen. Die einzelnen Flächeninhalte können Sie in dieser Situation dann mit Formeln für Dreiecke oder Rechtecke berechnen.
Der Integralwert ergibt sich dann als Summe der Teilflächen, die oberhalb der
-Achse liegen, abzüglich der Summe der Teilflächen, die unterhalb der
-Achse liegen. In diesem Sinne kann man den Integralwert als die Summe
vorzeichenbehafteter Flächenwerte verstehen.
Der Integralwert von ist .
.
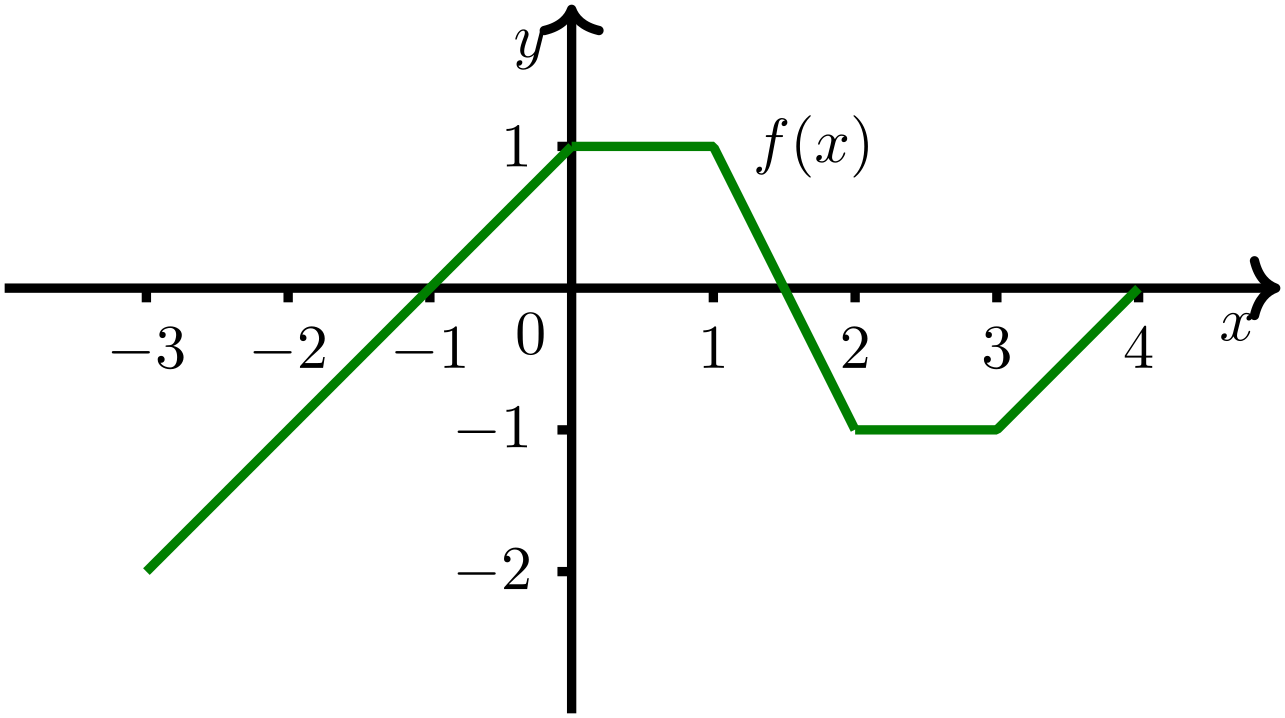
Berechnen Sie zu mit dem unten dargestellten Graphen das Integral mit Methoden aus der elementaren Geometrie, indem Sie die entsprechende Fläche „unter dem Graphen der Funktion“ in elementare geometrische Flächen wie Dreiecke oder Rechtecke zerlegen, die entweder oberhalb oder unterhalb der -Achse liegen. Die einzelnen Flächeninhalte können Sie in dieser Situation dann mit Formeln für Dreiecke oder Rechtecke berechnen.

Abbildung 8.2.4: Skizze (C)
Der Integralwert von ist
Aufgabe 8.2.17
Berechnen Sie die folgenden Integrale:
Berechnen Sie die folgenden Integrale:
-
 ,
,
-
 ,
,
-
 ,
,
-
 .
.
Aufgabe 8.2.18
Der Wert des Integrals ist .
.
Der Wert des Integrals ist
Aufgabe 8.2.19
Berechnen Sie eine reelle Zahl so, dass der Integralwert
den Wert ergibt: Der Wert für ist .
.
Berechnen Sie eine reelle Zahl so, dass der Integralwert
den Wert ergibt: Der Wert für ist
Aufgabe 8.2.20
Berechnen Sie die Integrale:
Berechnen Sie die Integrale:
-
 ,
,
-
 .
.
Aufgabe 8.2.21
Der Wert des Integrals ist .
.
Der Wert des Integrals ist
Aufgabe 8.2.22
Berechnen Sie die Integrale
Berechnen Sie die Integrale
-
 ,
,
-
 .
.
Aufgabe 8.2.23
Berechnen Sie das Integral
 .
.
Berechnen Sie das Integral