2. Elementare Funktionen
  3. Eigenschaften und Konstruktion elementarer Funktionen
  4. Summen, Produkte, Verkettungen

6.6.3 Summen, Produkte, Verkettungen

In diesem Abschnitt wollen wir nun das große Sortiment an elementaren Funktionen, die wir uns in diesem Modul erarbeitet haben, nutzen, um neue komplexere Funktionen aus den elementaren zu konsturieren. An verschiedenen Stellen im Verlauf dieses Moduls haben wir bereits Funktionen untersucht, deren Abbildungsvorschriften durch Summen- oder Produktbildung aus einfacheren Abbildungsvorschriften zusammengesetzt sind. Man kann natürlich auch Differenzen und unter bestimmten Umständen Quotienten von Abbildungsvorschriften bilden. Das folgende Beispiel stellt nochmal einige solche zusammengesetzte Funktionen zusammen.

Beispiel 6.6.4  
  • Die Funktion

    f:  { ℝ→ℝ x⟼x+sin(x)

    ist die Summe aus der Identität (vgl. Abschnitt 6.2.3) und der Sinusfunktion (vgl. Abschnitt 6.5). Sie besitzt den folgenden Graphen:

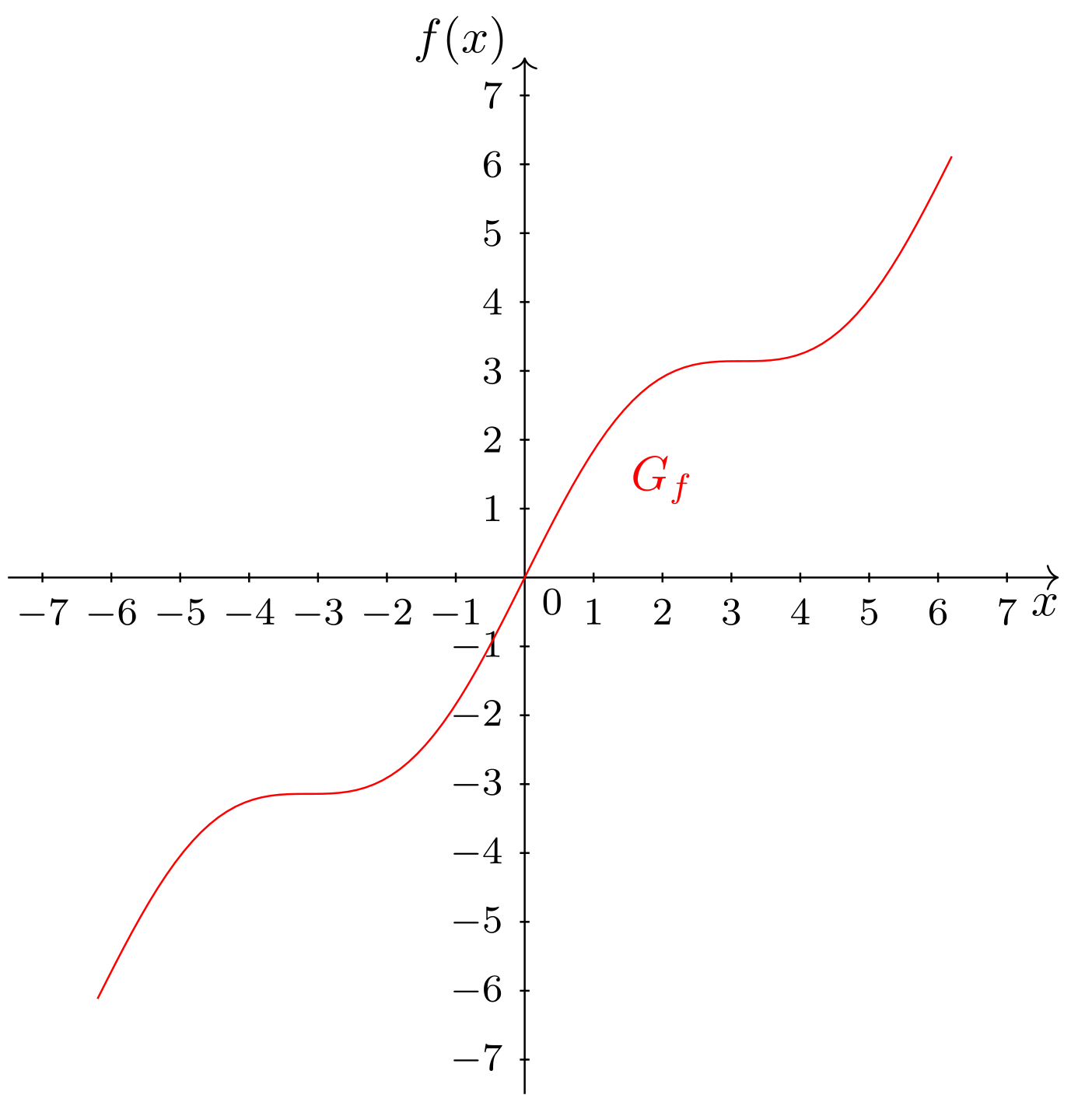    ./_2962713D_4x.png
    Abbildung 6.6.3: Skizze  (C)



  • Die Funktion

    g:  { [1;2]→ℝ y⟼ y2 -ln(y)

    ist die Differenz aus der Standardparabel (vgl. Abschnitt 6.2.6) und der natürlichen Logarithmusfunktion (vgl. Abschnitt 6.4.4). Sie besitzt den folgenden Graphen:
    ./_EAA2965A_4x.png
    Abbildung 6.6.4: Skizze  (C)



  • Die Funktion

    h:  { (0;∞)→ℝ x⟼ex 1 x

    ist das Produkt aus der natürlichen Exponentialfunktion mit Abbildungsvorschrift ex (vgl. Abschnitt 6.4.3) und der Hyperbel mit Abbildungvorschrift 1 x (vgl. Abschnitt 6.2.8). Sie besitzt folgenden Graphen:

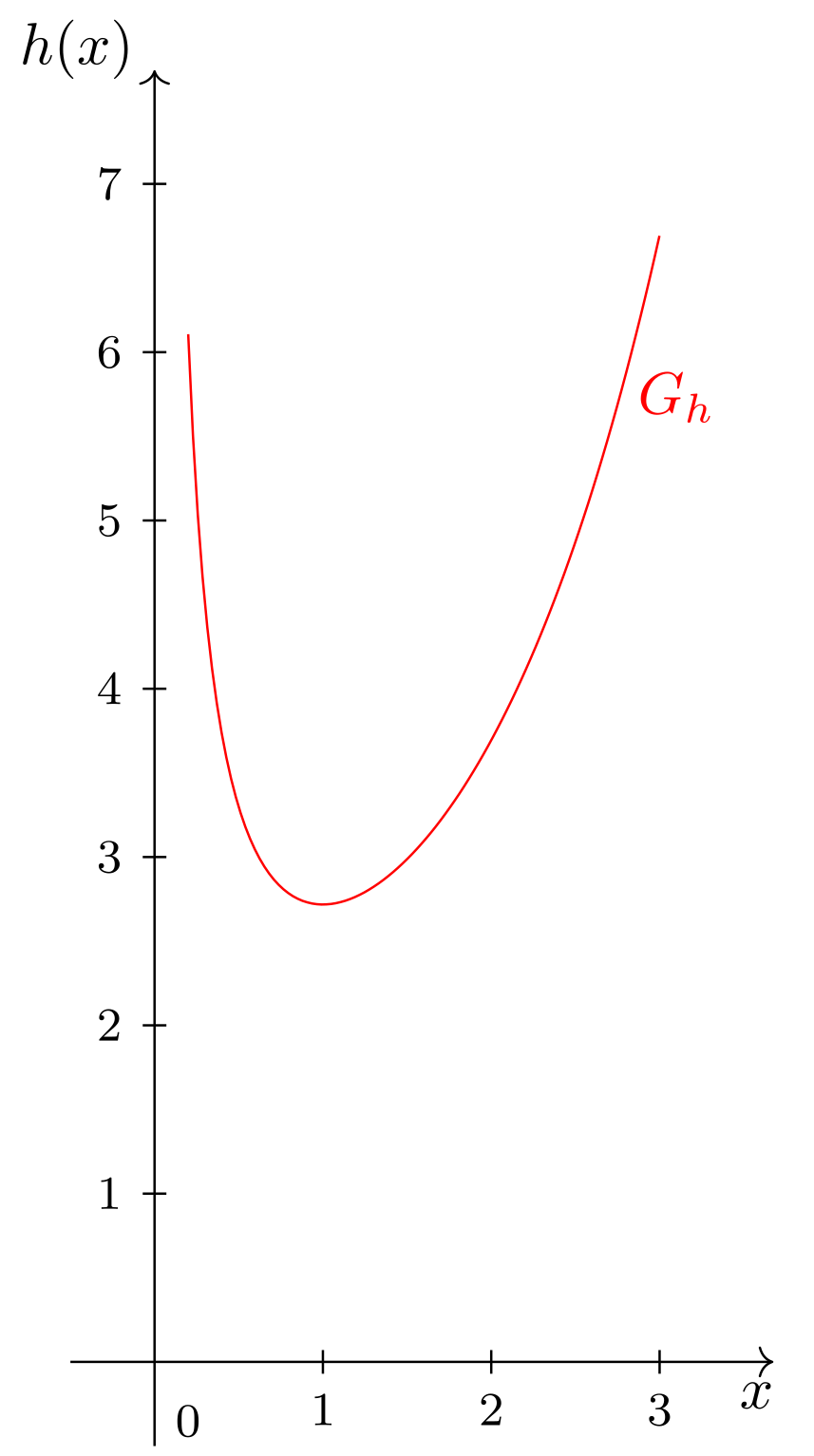    ./_2F3647AA_4x.png
    Abbildung 6.6.5: Skizze  (C)



  • Die Funktion

    φ:  { ℝ→ℝ z⟼ cos(z) z2 +1

    ist der Quotient aus der Cosinusfunktion (vgl. Abschnitt 6.5.3) und dem Polynom zweiten Grades (vgl. Abschnitt 6.2.7) mit der Abbildungsvorschrift z2 +1. Sie besitzt folgenden Graphen:

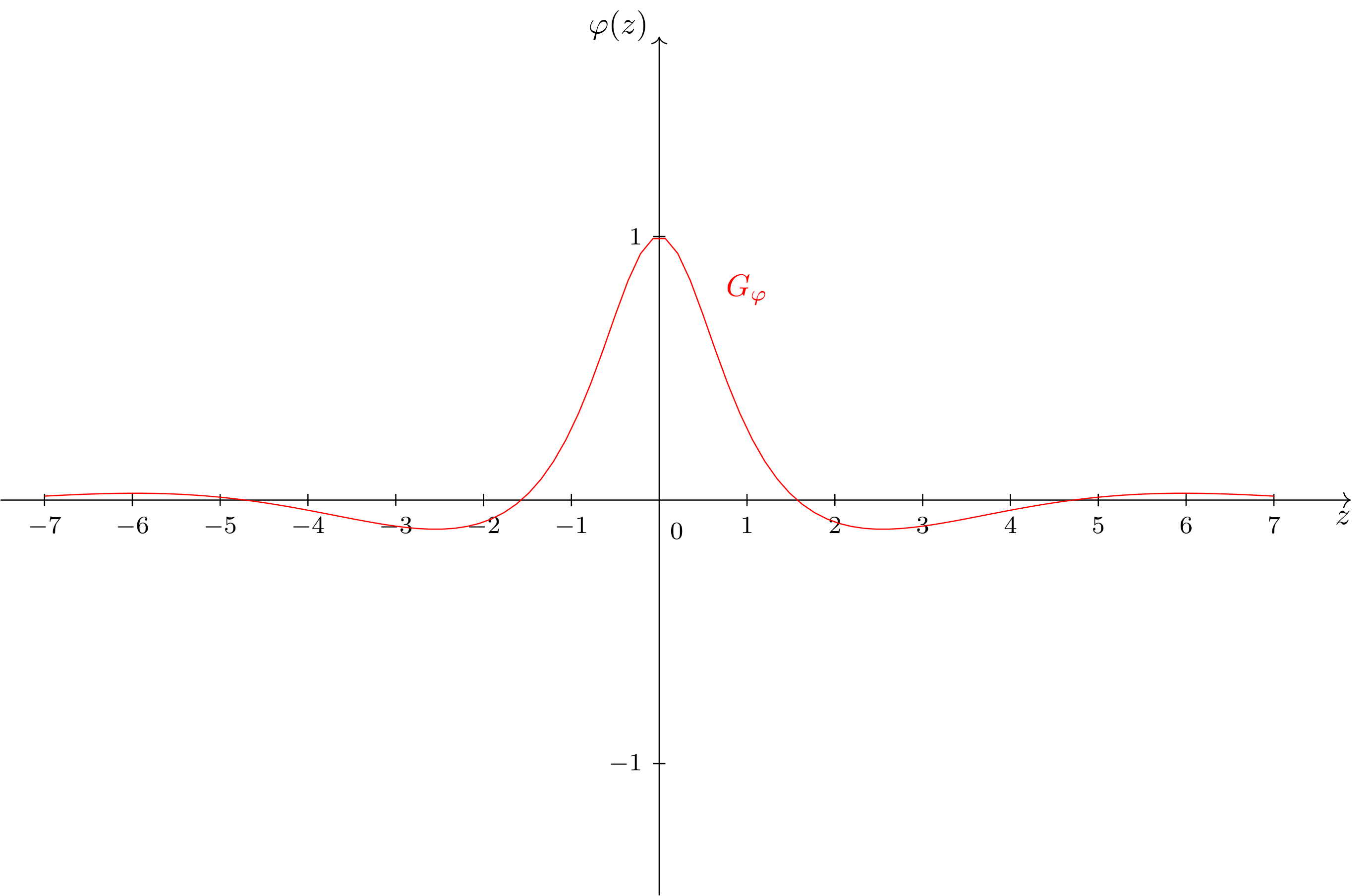    ./_C66DAAC4_4x.png
    Abbildung 6.6.6: Skizze  (C)







Aufgabe 6.6.5  
Finden Sie weitere Beispiele in diesem Modul für bereits behandelte elementare Funktionen, die mittels Summen-, Differenz-, Produkt- oder Quotientenbildung aus einfacheren elementaren Funktionen hervorgehen.





Zuletzt gibt es noch eine weitere Art, elementare Funktionen zu verknüpfen um neue Funktionen zu erhalten. Dies ist die sogenannte Verkettung oder Komposition von Funktionen.

Wir betrachten dazu einige Beispiele.

Beispiel 6.6.6  
  • Die Funktionen

    f:  { ℝ→ℝ x⟼f(x)= x2 +1

    und

    g:  { ℝ→ℝ x⟼g(x)=ex

    lassen sich auf zweierlei Art verketten. Wir können die Funktion f∘g:ℝ→ℝ oder die Funktion g∘f:ℝ→ℝ bilden. Wir erhalten

    (f∘g)(x)=f(g(x))=f(ex )=(ex )2 +1=e2x +1 ,

    also

    f∘g:  { ℝ→ℝ x⟼e2x +1

    und

    (g∘f)(x)=g(f(x))=g( x2 +1)=e x2 +1  ,

    also

    g∘f:  { ℝ→ℝ x⟼e x2 +1  .

    Anhand der Graphen sehen wir, dass dies zwei völlig unterschiedliche Funktionen sind. Es kommt also auf die Reihenfolge der Verkettung an.

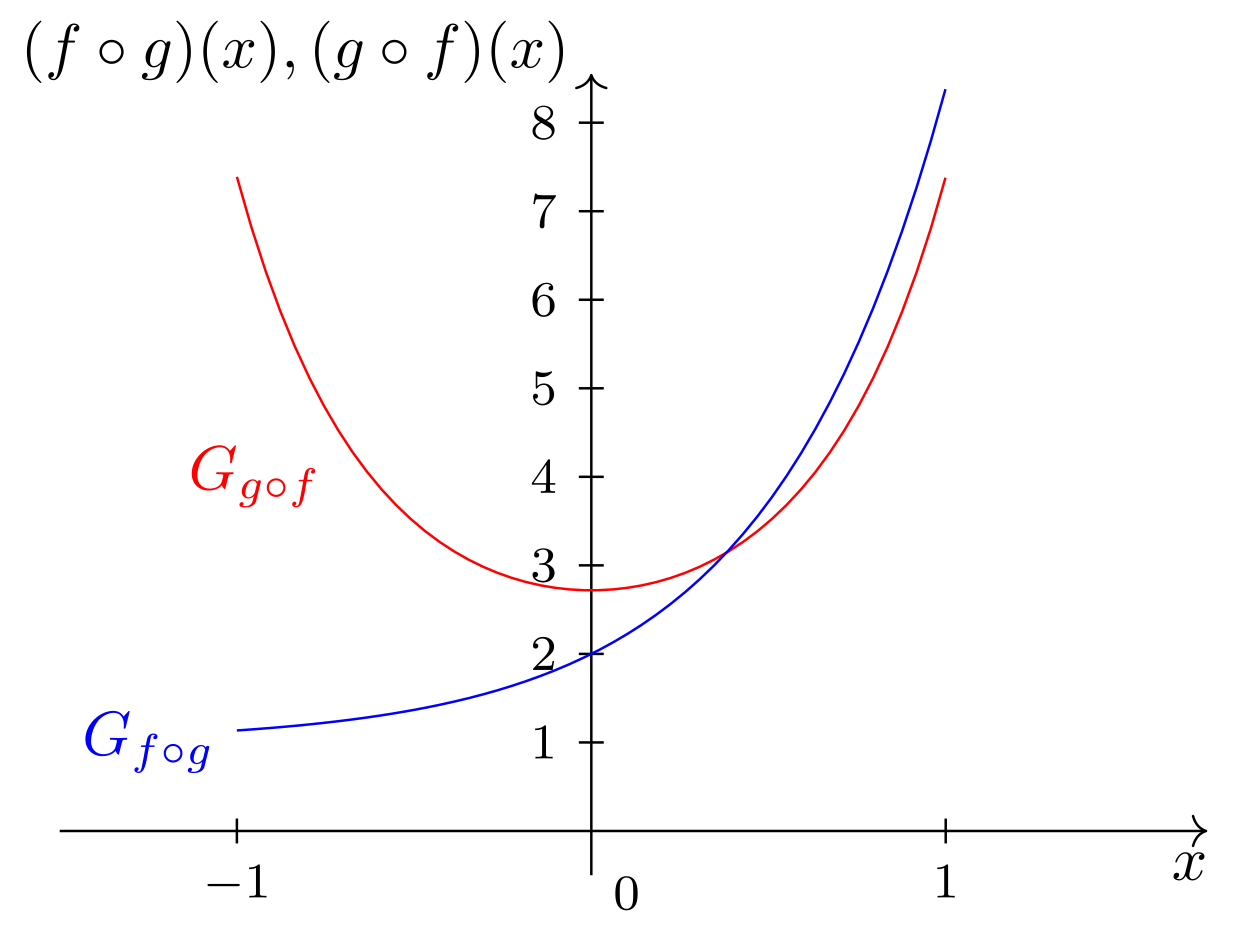    ./_EE81CB00_4x.png
    Abbildung 6.6.7: Skizze  (C)



  • Bei zwei Funktionen wie

    h:  { ℝ→ℝ x⟼sin(x)

    und

    w:  { [0;∞)→ℝ x⟼x

    ist allerdings auf die Definitionsbereiche bei der Verkettung zu achten. Denn wollen wir etwa die verkettete Funktion w∘h betrachten, so gilt

    (w∘h)(x)=w(h(x))=w(sin(x))=sin(x) .

    Da die Funktionswerte des Sinus aber auch negativ werden können, man aber in die Quadratwurzelfunktion nur nicht-negative Werte einsetzen darf, muss also der Definitionsbereich der Sinusfunktion entsprechend eingeschränkt werden, so dass sich nicht-negative Werte ergeben, zum Beispiel mittels x∈[0;π]= Dw∘h . Wir erhalten also

    w∘h:  { [0;π]→ℝ x⟼sin(x) .





Aufgabe 6.6.7  
Gegeben sind die Funktionen

f:  { ℝ→ℝ x⟼2x-3 



g:  { ℝ∖{0}→ℝ x⟼ 1 x



und

h:  { ℝ→ℝ x⟼sin(x) .

Bestimmen Sie die Verkettungen f∘g, g∘f, h∘f, h∘g, f∘f und g∘g. Schränken Sie dazu eventuell die Definitionsbereiche so ein, dass die Verkettung zulässig ist. Benutzen Sie jedoch für die verketteten Funktion stets die größtmöglichen Definitionsbereiche.