7.2.3 Ableitung spezieller Funktionen
Ableitung trigonometrischer Funktionen
Die Sinusfunktion , ist periodisch mit Periode . Somit genügt es, die Funktion auf einem Intervall der Länge zu betrachten. Einen Ausschnitt des Graphen für zeigt die folgende Abbildung:
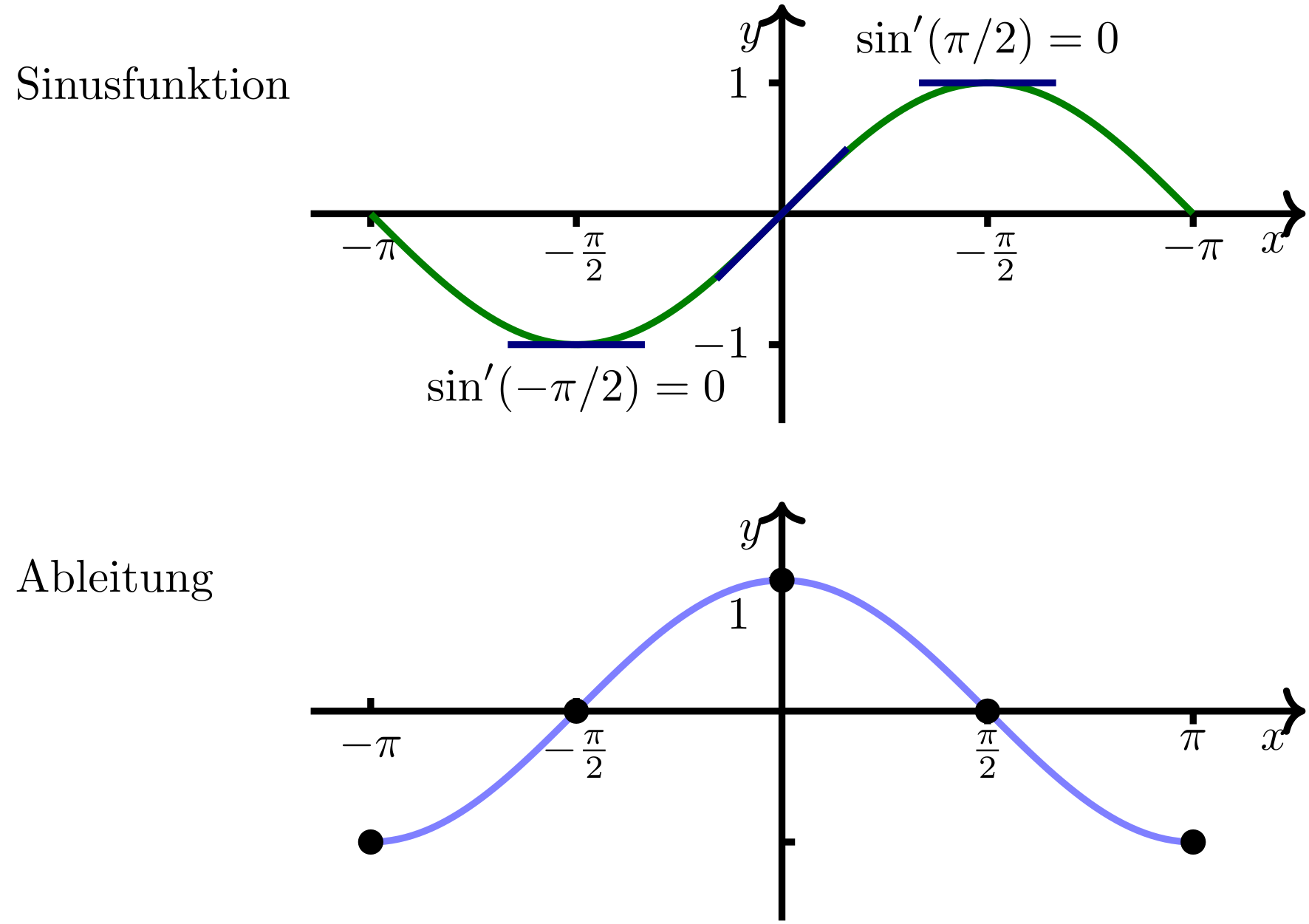
Abbildung 7.2.2: Skizze (C)
Wie in der Abbildung zu sehen, ist die Steigung des Sinus bei gerade . Legt man eine Tangente an der Stelle an den Graphen der Sinusfunktion, erhält man als deren Steigung . Untersucht man die Stellen , so findet man, dass dort die gleiche Steigung wie bei , aber mit umgedrehtem Vorzeichen, vorliegt. Die Steigung ist dort also . Die Ableitung des Sinus ist also eine Funktion, die genau diese Eigenschaften erfüllt. Eine genaue Untersuchung der Bereiche zwischen diesen speziell ausgesuchten Stellen ergibt, dass der Kosinus die Ableitung des Sinus darstellt:
Ableitung trigonometrischer Funktionen
7.2.5
Für die Sinusfunktion , gilt
Für die Kosinusfunktion , gilt
Für die Tangensfunktion , gilt
Für die Sinusfunktion , gilt
Für die Kosinusfunktion , gilt
Für die Tangensfunktion , gilt
Ableitung der Exponentialfunktion
Info
7.2.6
Die Exponentialfunktion , hat die besondere Eigenschaft, dass ihre Ableitung wiederum die Exponentialfunktion ist, also gilt.
Die Exponentialfunktion , hat die besondere Eigenschaft, dass ihre Ableitung wiederum die Exponentialfunktion ist, also gilt.
Ableitung der Logarithmusfunktion
Die Ableitung der Logarithmusfunktion wird hier ohne Beweis angegeben. Für mit erhält man , .


