11.2.4 Stetige Verzinsung

Der Ausdruck $a_n={(1+\frac{r}{n})}^n$ mit $r\in ℝ$ lässt sich in Abhängigkeit von $n\in \mathbb{N}$ auch auffassen als Abbildung

${\displaystyle a:\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathbb{N}\hspace{0.5em}\to \hspace{0.5em}ℝ\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}},\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}}n\hspace{0.5em}⟼\hspace{0.5em}a(n)\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{a}_n\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{(1+\frac{r}{n})}^n\hspace{0.5em}.}$

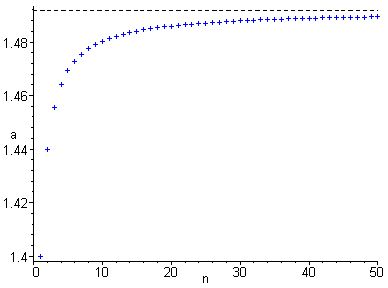
Eine Abbildung $\mathbb{N}\ni n\mapsto a_n\in ℝ$ nennt man eine reelle Zahlenfolge. Die Paare $(n,a_n)$ für $n\in \mathbb{N}$ lassen sich interpretieren als Punkte in der euklidischen Ebene. Im folgenden Bild ist die Folge $a_n={(1+\frac{0.4}{n})}^n$ in diesem Sinn als Punktfolge in der euklidischen Ebene dargestellt:



An diesem Bild erkennt man zwei Eigenschaften dieser Folge:

• Die Folge $a_n$, $n\in \mathbb{N}$, ist monoton wachsend, d.h. aus $i\le j$ folgt $a_i\le a_j$ für $i,j\in \mathbb{N}$.
  
  
• Die Folge nähert sich für wachsende $n\in \mathbb{N}$ beliebig genau einem Wert $a\in ℝ$ an. Diese Zahl $a$ nennt man den Grenzwert der Folge $a_n$ und man schreibt
  
  ${\displaystyle \underset{n\to \infty }{lim}{a}_n\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}a\hspace{0.5em}.}$
  
  
  
  

In der Vorlesung Mathematik 1 wird die natürliche Exponentialfunktion

${\displaystyle \exp :\mathrm{\hspace{0.5em}\hspace{0.5em}}ℝ\hspace{0.5em}\to \hspace{0.5em}ℝ\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}},\mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{\hspace{0.5em}\hspace{0.5em}}x\hspace{0.5em}⟼\hspace{0.5em}\exp (x)\hspace{0.5em}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{e}^x}$

vollständig eingeführt.



Dort wird die folgende Aussage gezeigt:



Für $x=1$ ergibt dieser Grenzwert die Eulersche Zahl, benannt nach dem Schweizer Mathematiker Leonhard Euler (1707 - 1783):

${\displaystyle \underset{n\to \infty }{lim}{(1+\frac{1}{n})}^n\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}e\mathrm{\hspace{0.5em}\hspace{0.5em}}\approx \mathrm{\hspace{0.5em}\hspace{0.5em}}\mathrm{2,7182}\dots \hspace{0.5em}.}$

Man kann zeigen (schwierig), dass die Eulersche Zahl $e$ eine irrationale Zahl ist und sich daher nicht als Bruch schreiben lässt.

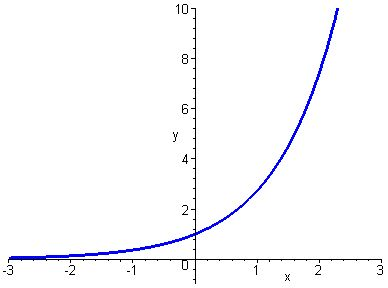
Die Exponentialfunktion erfüllt die Potenzgesetze für beliebige reelle Zahlen als Exponenten:

• $\exp (x+y)=e^{x+y}=e^x·e^y=\exp (x)·\exp (y)$ für $x,y\in ℝ$.
  
  
• $\exp (x·y)=e^{x·y}={\left(e^x\right)}^y={\left(e^y\right)}^x$ für $x,y\in ℝ$.
  
  

Mit Hilfe der Exponentialfunktion und dem Zusammenhang mit der Folge $(1+\frac{x}{n}{)}^n$ kann man Informationen über den Verzinsungsvorgang erhalten wenn die Anzahl der Zeitpunkte $n$ sehr groß wird: Das Kapital wird jährlich mit einem Faktor ${(1+\frac{r}{n})}^n$ multipliziert, wenn die Zinsen mit der Rate $\frac{r}{n}$ dem Anfangskapital $S_0$ an $n$ verschiedenen Zeitpunkten des Jahres gutgeschrieben werden. Nach $t$ Jahren, $t\in \mathbb{N}$, ist das Kapital angewachsen auf

${\displaystyle S_0·{(1+\frac{r}{n})}^{n·t}\hspace{0.5em}.}$

Für $n\to \infty$ ergibt sich der Grenzwert

${\displaystyle \underset{n\to \infty }{lim}(S_0·{(1+\frac{r}{n})}^{n·t})\mathrm{\hspace{0.5em}\hspace{0.5em}}=\mathrm{\hspace{0.5em}\hspace{0.5em}}{S}_0·e^{r·t}\hspace{0.5em}.}$

Bei wachsendem $n\in \mathbb{N}$ werden die Zinsen immer häufiger gutgeschrieben: