5.4.4 Umfang
Der Umfang eines Vielecks ist die Summe der Längen aller Verbindungsstecken.
Wenn ein Vieleck weitere Eigenschaften hat, die einen Bezug zur Länge der
Seiten haben, kann es weitere Aussagen zum Umfang geben.
Es werden zunächst Vierecke betrachtet. Wenn und benachbarte Seiten eines Parallelogramms sind, dann ist sein Umfang .
Bei einer Raute und auch bei einem Quadrat sind alle vier Seiten gleich lang, sodass sein Umfang durch gegeben ist, wenn die Länge einer Seite ist.
Ebenso sind bei jedem regelmäßigen Vieleck alle Seiten gleich lang. Wenn die Anzahl der Eckpunkte und die Länge einer Seite ist, dann ist der Umfang einfach durch zu berechnen.
Als Ausblick auf die Winkelfunktionen, die im Abschnitt 5.6 besprochen werden, soll der Umfang eines regelmäßigen Vielecks noch auf eine andere Weise berechnet werden. Seine Ecken liegen alle auf einem Kreis mit einem Radius .
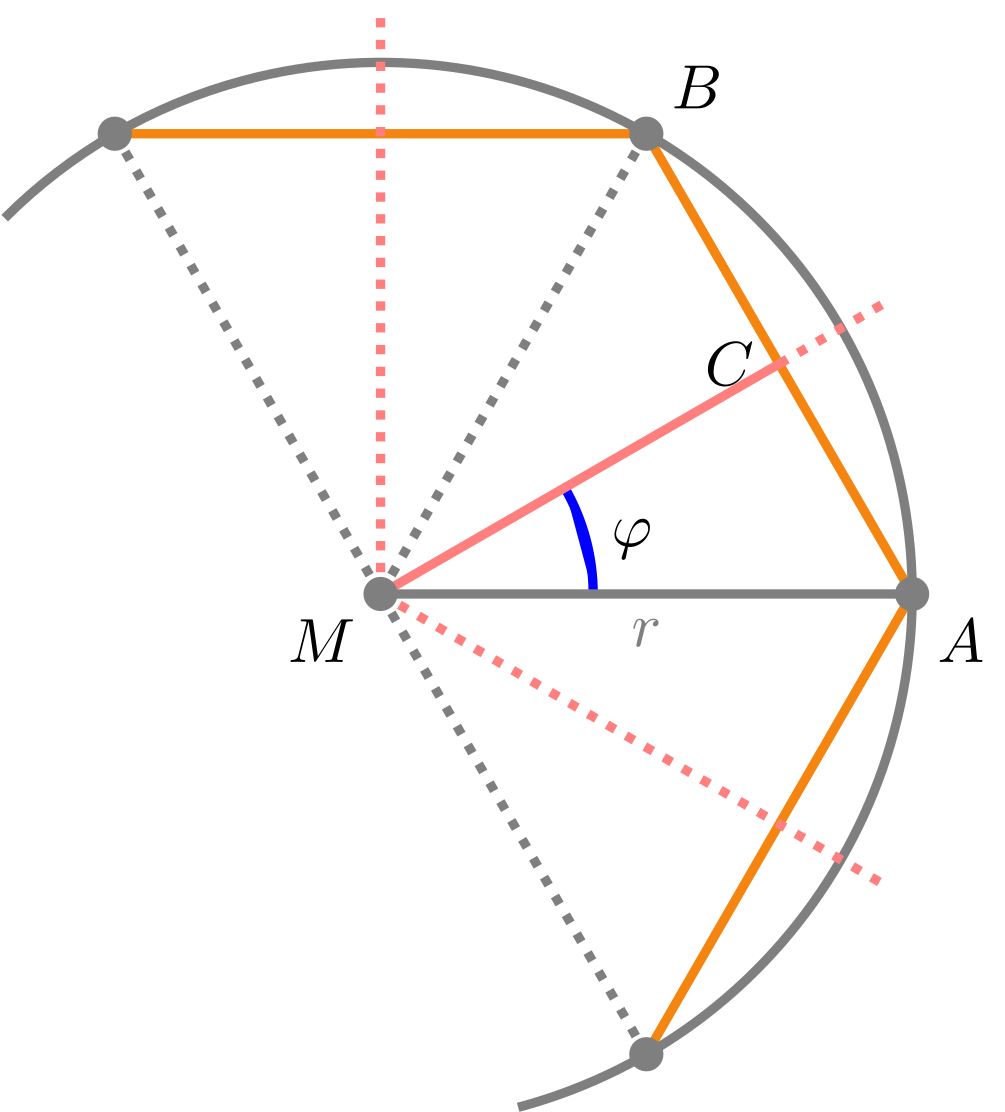
Der Winkel zwischen den Strecken, die vom Mittelpunkt des Kreises zu den Ecken und einer Seite verlaufen, ist der -te Teil des Vollwinkels: . Der Mittelpunkt des Kreises, und der Mittelpunkt der Strecke bilden ein rechtwinkliges Dreieck mit dem Winkel . Wenn aus
der Wert von berechnet und in eingesetzt wird, erhält man die Formel
für den Umfang eines regelmäßigen Vielecks. Beispielsweise ist . Je größer ist, um so mehr nähert sich der Umfang des Vielecks dem Wert an, der den Umfang eines Kreises mit Radius angibt. Dies kann mit weiterführenden Methoden der Differentialrechnung begründet werden, in deren Grundideen im Kapitel 7 eingeführt wird. Die Idee hinter der beschriebenen Annäherung kann man hier so beschreiben: Zu einem schwierig zu berechnenden Wert wie dem Kreisumfang sucht man nach vielen vergleichbaren Objekten, hier den regelmäßigen Vielecken, die zwei Eigenschaften haben: Ihr Umfang ist einfach zu berechnen, und bei hinreichend großer Eckenzahl unterscheiden sie sich hinsichtlich des Umfangs vom Kreis um weniger als irgend eine vorgegebene positive Zahl (hier denkt man an „kleine“ Zahlen). Dieses Vorgehen eignet sich auch für die Berechnung von Flächen, die nicht durch Strecken berandet werden (siehe Kapitel 8). Dazu wird im Folgenden zunächst die Berechnung von Flächeninhalten von Vielecken erläutert, die in dieser Hinsicht relativ einfach ist und die Ausgangspunkt für eine Annäherung sein kann, wie das obige Bild eines Sechsecks in einem Kreis zeigt.
Es werden zunächst Vierecke betrachtet. Wenn und benachbarte Seiten eines Parallelogramms sind, dann ist sein Umfang .
Bei einer Raute und auch bei einem Quadrat sind alle vier Seiten gleich lang, sodass sein Umfang durch gegeben ist, wenn die Länge einer Seite ist.
Ebenso sind bei jedem regelmäßigen Vieleck alle Seiten gleich lang. Wenn die Anzahl der Eckpunkte und die Länge einer Seite ist, dann ist der Umfang einfach durch zu berechnen.
Als Ausblick auf die Winkelfunktionen, die im Abschnitt 5.6 besprochen werden, soll der Umfang eines regelmäßigen Vielecks noch auf eine andere Weise berechnet werden. Seine Ecken liegen alle auf einem Kreis mit einem Radius .

Abbildung 5.4.9: Skizze (C)
Der Winkel zwischen den Strecken, die vom Mittelpunkt des Kreises zu den Ecken und einer Seite verlaufen, ist der -te Teil des Vollwinkels: . Der Mittelpunkt des Kreises, und der Mittelpunkt der Strecke bilden ein rechtwinkliges Dreieck mit dem Winkel . Wenn aus
der Wert von berechnet und in eingesetzt wird, erhält man die Formel
für den Umfang eines regelmäßigen Vielecks. Beispielsweise ist . Je größer ist, um so mehr nähert sich der Umfang des Vielecks dem Wert an, der den Umfang eines Kreises mit Radius angibt. Dies kann mit weiterführenden Methoden der Differentialrechnung begründet werden, in deren Grundideen im Kapitel 7 eingeführt wird. Die Idee hinter der beschriebenen Annäherung kann man hier so beschreiben: Zu einem schwierig zu berechnenden Wert wie dem Kreisumfang sucht man nach vielen vergleichbaren Objekten, hier den regelmäßigen Vielecken, die zwei Eigenschaften haben: Ihr Umfang ist einfach zu berechnen, und bei hinreichend großer Eckenzahl unterscheiden sie sich hinsichtlich des Umfangs vom Kreis um weniger als irgend eine vorgegebene positive Zahl (hier denkt man an „kleine“ Zahlen). Dieses Vorgehen eignet sich auch für die Berechnung von Flächen, die nicht durch Strecken berandet werden (siehe Kapitel 8). Dazu wird im Folgenden zunächst die Berechnung von Flächeninhalten von Vielecken erläutert, die in dieser Hinsicht relativ einfach ist und die Ausgangspunkt für eine Annäherung sein kann, wie das obige Bild eines Sechsecks in einem Kreis zeigt.


