6.3.2 Wurzelfunktionen
Beispiel
6.3.1
Untersucht man einen Körper, der sich im freien Fall im homogenen Gravitationsfeld der Erde befindet, so kann man folgenden Zusammenhang zwischen seiner Fallzeit und seinem zurückgelegten Weg feststellen:
Dabei ist die physikalische Konstante der Fallbeschleunigung. Trägt man nun diese Werte in einem Diagramm mit auf der Hochachse und auf der Querachse auf, erhält man:

Dies legt nahe, dass man den Zusammenhang zwischen und , mit als Veränderlicher, mathematisch durch die Funktion
beschreiben kann, also eine Funktion, in deren Abbildungsvorschrift die Wurzel (genauer gesagt die Quadratwurzel) der Veränderlichen vorkommt. Deren Graph beinhaltet dann die obigen gemessenen Punkte:
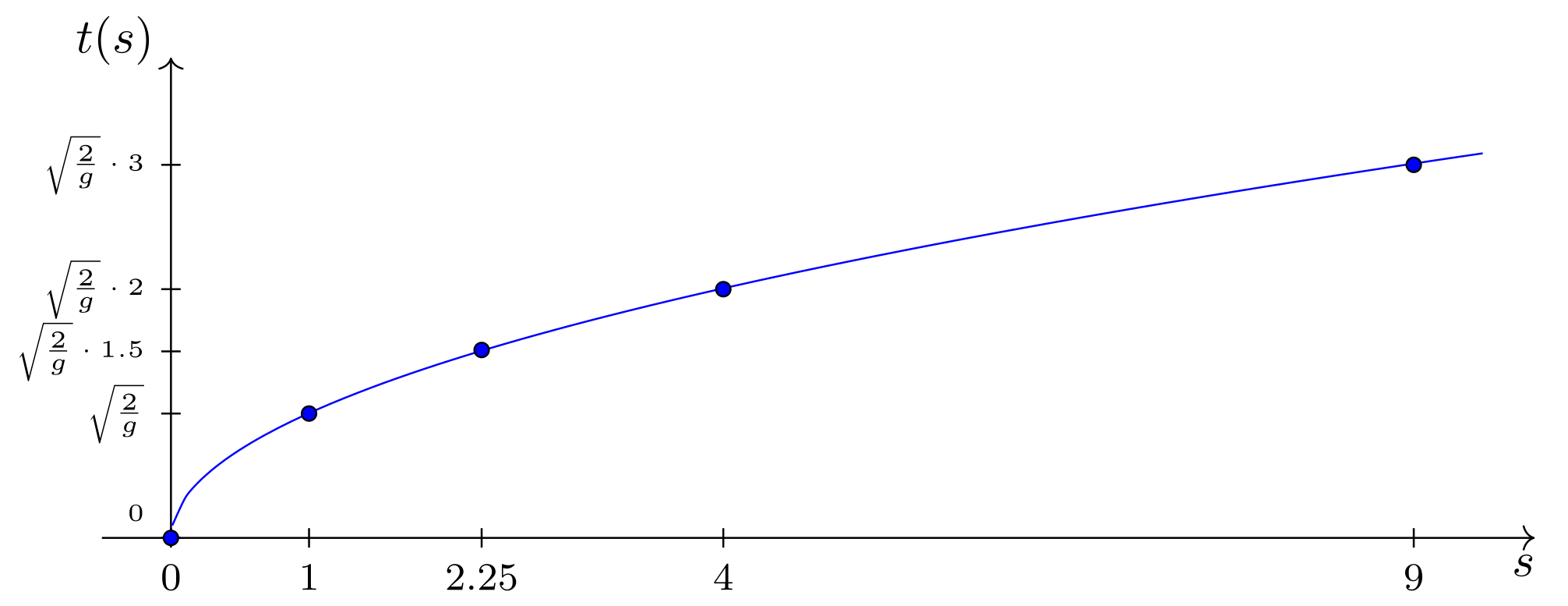
Untersucht man einen Körper, der sich im freien Fall im homogenen Gravitationsfeld der Erde befindet, so kann man folgenden Zusammenhang zwischen seiner Fallzeit und seinem zurückgelegten Weg feststellen:
| Fallzeit in Sekunden | |||||
| zurückgelegter Weg in Metern |
Dabei ist die physikalische Konstante der Fallbeschleunigung. Trägt man nun diese Werte in einem Diagramm mit auf der Hochachse und auf der Querachse auf, erhält man:

Abbildung 6.3.1: Skizze (C)
Dies legt nahe, dass man den Zusammenhang zwischen und , mit als Veränderlicher, mathematisch durch die Funktion
beschreiben kann, also eine Funktion, in deren Abbildungsvorschrift die Wurzel (genauer gesagt die Quadratwurzel) der Veränderlichen vorkommt. Deren Graph beinhaltet dann die obigen gemessenen Punkte:

Abbildung 6.3.2: Skizze (C)
Dieses Beispiel zeigt, dass Funktionen mit Abbildungsvorschriften, die Wurzeln der Veränderlichen enthalten, natürlicherweise in Anwendungen der Mathematik auftauchen.
Für natürliche Zahlen , bezeichnet man die Funktionen
als die Klasse der Wurzelfunktionen. Diese beinhalten offenbar die Quadratwurzel , die dritte Wurzel , die vierte Wurzel , usw. als Abbildungsvorschriften von Funktionen (vgl. Potenzgesetze).
Aufgabe 6.3.2
Benutzen Sie die Potenzrechengesetze, um die Abbildungsvorschrift der Wurzelfunktionen ohne Wurzelzeichen und stattdessen mit Hilfe von Exponenten aufzuschreiben.
Benutzen Sie die Potenzrechengesetze, um die Abbildungsvorschrift der Wurzelfunktionen ohne Wurzelzeichen und stattdessen mit Hilfe von Exponenten aufzuschreiben.
Aufgabe 6.3.3
Welche Funktion ergäbe sich für ?
Welche Funktion ergäbe sich für ?
Von großem Interesse ist nun der größtmögliche Definitionsbereich , der für diese Wurzelfunktionen möglich ist. Denn offenbar kommt es auf den Wurzelexponenten an, welche Werte man für in die Abbildungsvorschriften einsetzen darf, um reelle Werte als Ergebnisse zu erhalten. So erkennen wir, dass bei der Quadratwurzel nur nicht-negative Werte ein reelles Ergebnis liefern. Betrachten wir allerdings die Kubikwurzel , so erhalten wir in diesem Fall, dass alle reellen Zahlen eingesetzt wieder reelle Zahlen als Ergebnis liefern, so etwa . Allgemein gilt:
Info
6.3.4
Die Wurzelfunktionen
mit und besitzen den größtmöglichen Definitionsbereich falls gerade ist und falls ungerade ist.
Die Wurzelfunktionen
mit und besitzen den größtmöglichen Definitionsbereich falls gerade ist und falls ungerade ist.
Damit erhält man folgendes Aussehen für die Graphen der ersten vier Wurzelfunktionen :
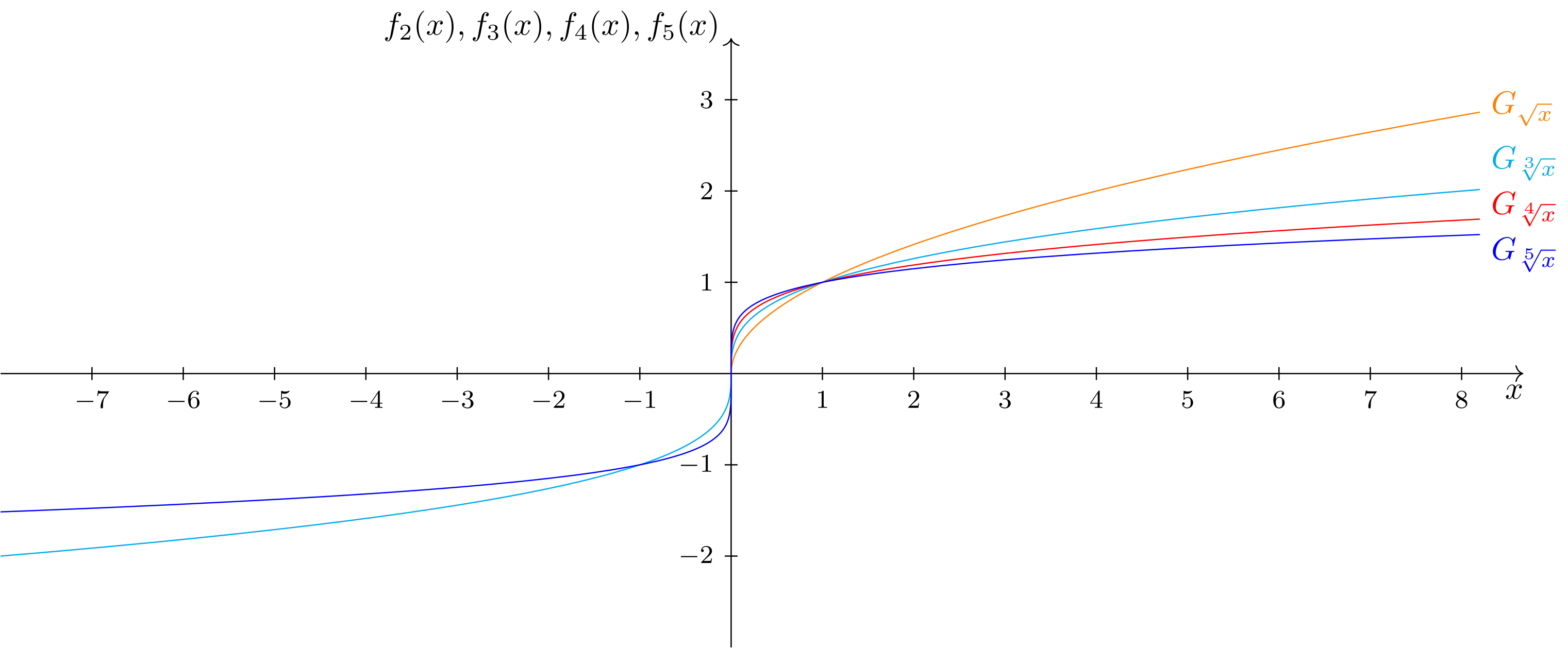
Abbildung 6.3.3: Skizze (C)
Aus dem Verlauf der Graphen sieht man, dass alle Wurzelfunktionen streng monoton wachsend sind.
Aufgabe 6.3.5
Bestimme für die Wurzelfunktionen
mit , , den Wertebereich , in Abhängigkeit davon ob gerade oder ungerade ist.
Bestimme für die Wurzelfunktionen
mit , , den Wertebereich , in Abhängigkeit davon ob gerade oder ungerade ist.


