2.2.3 Gemischte Gleichungen

Info 2.2.6

Treten in einer Gleichung Beträge zusammen mit anderen Ausdrücken auf, so sind die Fallunterscheidungen passend zu den Termen in den Beträgen einzurichten und nur auf diese anzuwenden.

Dabei darf man nicht vergessen, die gefundenen Lösungsmengen mit den Fallbedingungen abzugleichen:

Beispiel 2.2.7
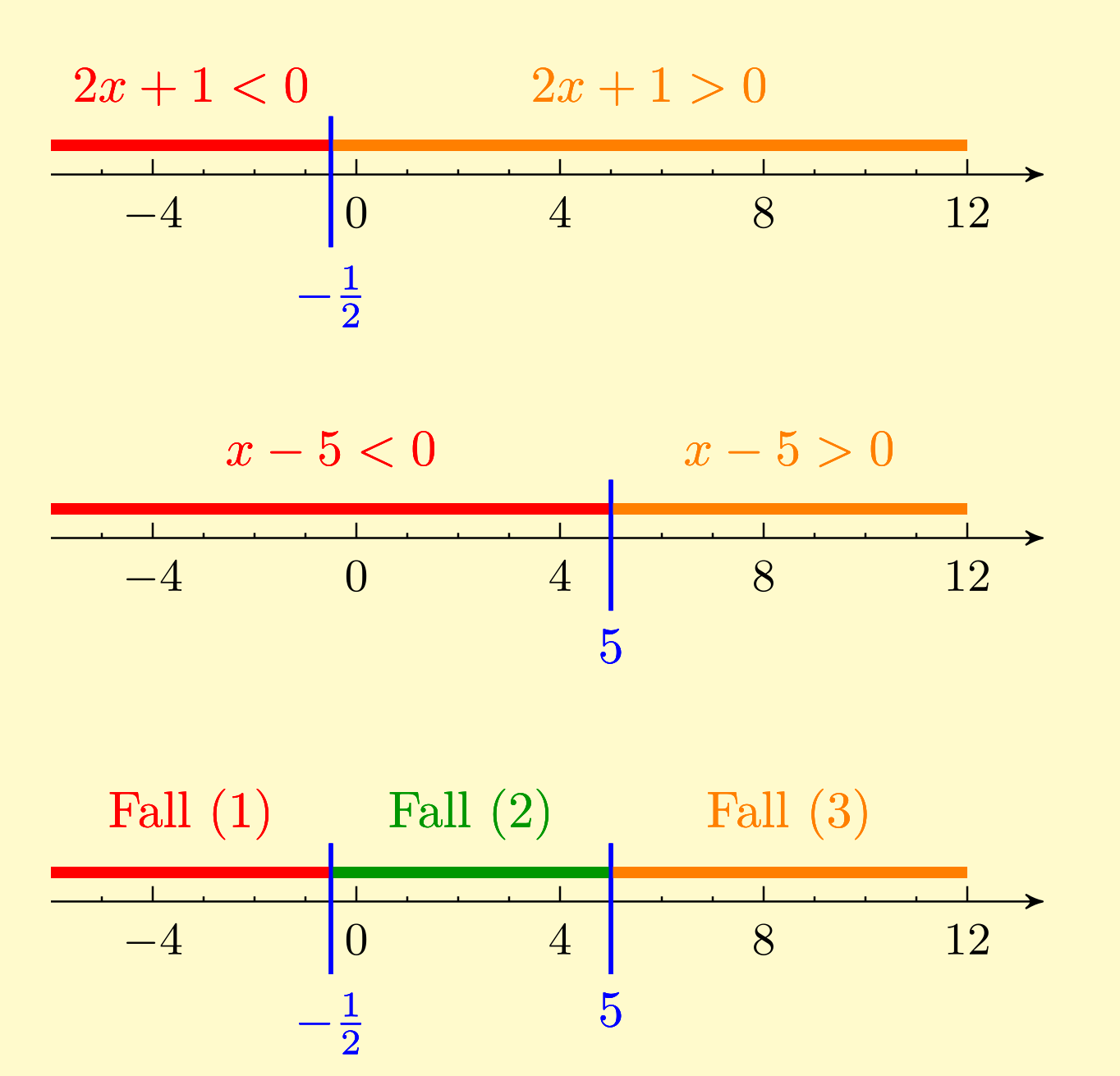
Zu lösen sei die Gleichung

| x - 1 | + x^{2} = 1

. Die Fallunterscheidung lautet hier wie folgt:

Ist $x \geq 1$ , so kann man den Betrag durch Klammern ersetzen und erhält die quadratische Gleichung $(x - 1) + x^{2} = 1$ , welche zu $x^{2} + x - 2 = 0$ umgeformt wird. Die $p q$ -Formel liefert die beiden Lösungen

$x_1 & =& -\Mdfrac12-\sqrt{\Mdfrac94}\;=\; -2 \MDFPSpace, \\ x_2 & =& -\Mdfrac12+\sqrt{\Mdfrac94}\;=\; 1 \MDFPSpace,$
von denen nur $x_{2}$ die Fallbedingung erfüllt.
Ist $x < 1$ , so erhält man die Gleichung $- (x - 1) + x^{2} = 1$ , welche zu $x^{2} - x = 0$ bzw. $x \cdot (x - 1) = 0$ umgeformt wird. Man kann aus der Produktdarstellung die beiden Lösungen $x_{3} = 0$ und $x_{4} = 1$ ablesen, wegen der Fallbedingung ist hier nur $x_{3} = 0$ eine Lösung der ursprünglichen Gleichung.

Insgesamt ist also

L = {0; 1}

die Lösungsmenge der Ausgangsgleichung.

Aufgabe 2.2.8
Wie lautet die Lösungsmenge für die gemischte Gleichung

| x - 3 | \cdot x = 9

Ist $x \geq 3$ , so ist der Term im Betrag nicht negativ. Man erhält in diesem Fall die quadratische Gleichung

$=$ $0$ . Sie besitzt die Lösungsmenge

. Nur die Lösung

erfüllt die Fallbedingung.
Ist dagegen $x < 3$ , so ist der Term im Betrag negativ. Man erhält die normierte quadratische Gleichung

$=$ $0$ .
Sie besitzt die Lösungsmenge

.

Mengen können in aufzählender Form

{1; 2; 3}

eingegeben werden. Die Mengenklammer erhalten Sie mit AltGr+7 bzw. AltGr+0.

Damit ist die Lösungsmenge insgesamt

L

=

Ist

x

aus dem Intervall

[3; \infty [

, so ist der Term im Betrag nicht negativ und man erhält die quadratische Gleichung

x^{2} - 3 x - 9 = 0

mit Lösungsmenge

L = {\frac{3}{2} - \sqrt{\frac{45}{4}}; \frac{3}{2} + \sqrt{\frac{45}{4}}}

. Nur die größere Lösung

\frac{3}{2} + \sqrt{\frac{45}{4}}

erfüllt die Fallbedingung

x \geq 3

. Das sieht man auch ohne Taschenrechner an der Abschätzung

\sqrt{\frac{45}{4}} \geq \sqrt{\frac{36}{4}} = 3

. Ist

x

dagegen aus dem Intervall

] - \infty; 3 [

, so ist der Term im Betrag negativ. Man erhält die normierte quadratische Gleichung

x^{2} - 3 x + 9 = 0

. Sie ist wegen

\frac{1}{4} p^{2} - q < 0

in der

p q

-Formel unlösbar. Damit besitzt die ursprüngliche Gleichung nur die einzige Lösung

\frac{3}{2} + \sqrt{\frac{45}{4}}

Aufgabe 2.2.9
Untersuchen Sie die gemischte Betragsgleichung

3 | 2 x + 1 | = | x - 5 |

auf Lösungen, indem Sie die auftretenden Fälle auf dem Zahlenstrahl visualisieren und dann aufgrund einer Fallunterscheidung die Lösungen ermitteln. Visualisieren Sie zunächst die Fallunterscheidungen für die Einzelbeträge.

Die Lösungsmenge ist

Durch Untereinanderstellen der Fallunterscheidungen für die Betragsausdrücke

| 2 x + 1 |

und

| x - 5 |

kann man die insgesamt vorzunehmende Fallunterscheidung ablesen:

Abbildung 2.2.15: Skizze (C)

Graphische Darstellung der drei Fälle.

Man kann die folgenden drei Fälle ablesen:

Fall 1: $x < - \frac{1}{2}$ , hier sind die Terme in beiden Beträgen negativ.
Fall 2: $- \frac{1}{2} \leq x < 5$ , hier ist der Term im zweiten Betrag negativ, im ersten Betrag dagegen nicht.
Fall 3: $5 \leq x$ , hier sind beide Terme in den Beträgen nicht negativ.
Es gibt offenbar kein $x$ , für das der erste Term negativ, der zweite Term aber nicht negativ wird.

Damit kann man die Lösungen zusammenfassen:

Im Fall 1 drehen beide Beträge das Vorzeichen: $3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (- (2 x + 1)) = - (x - 5)$ .
Diese Gleichung hat die Lösung $x = - \frac{8}{5}$ , sie erfüllt die Fallbedingung.
Im Fall 2 dreht nur der zweite Betrag das Vorzeichen: $3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (2 x + 1) = - (x - 5)$ .
Diese Gleichung hat die Lösung $x = \frac{2}{7}$ , sie erfüllt die Fallbedingung.
Im Fall 3 kann man beide Beträge weglassen: $3 | 2 x + 1 | = | x - 5 | \Leftrightarrow 3 (2 x + 1) = (x - 5)$ .
Diese Gleichung hat die Lösung $x = - \frac{8}{5}$ , sie erfüllt nicht die Fallbedingung und wird daher innerhalb ihres Falles verworfen.

Die Lösungsmenge ist

{- \frac{8}{5}; \frac{2}{7}}

Online-Brückenkurs Mathematik

1 Elementares Rechnen

2 Gleichungen in einer Unbekannten

3 Ungleichungen in einer Unbekannten

4 Lineare Gleichungssysteme

5 Geometrie

6 Elementare Funktionen

7 Differentialrechnung

8 Integralrechnung

9 Orientierung im zweidimensionalen Koordinatensystem

10 Grundlagen der anschaulichen Vektorgeometrie

11 Grundlagen aus der Stochastik (Optional)

Eingangstest

Willkommen

Legende

2.2.3 Gemischte Gleichungen