6.2.10 Asymptoten

Beispiel 6.2.21  
Wir betrachten die Funktion

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{1\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & 1+\frac{1}{x-1}\hfill \end{array}}$
und stellen fest, dass deren Abbildungsvorschrift in der Form einer Summe aus einem Polynom (vom Grad $0$) und einem gebrochenrationalen Term vorliegt. Durch Bilden des Hauptnenners ist es nun einfach, $g(x)$ auf eine gebrochenrationale Form zu bringen, in der der Zählergrad und der Nennergrad gleich sind:

${\displaystyle g(x)=1+\frac{1}{x-1}=\frac{x-1}{x-1}+\frac{1}{x-1}=\frac{x-1+1}{x-1}=\frac{x}{x-1}\hspace{0.5em}.}$
Wir können $g$ also auch schreiben als

${\displaystyle g:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ\setminus \{1\}& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & \frac{x}{x-1}\hfill \end{array}}$


und betrachten den zugehörigen Graphen:




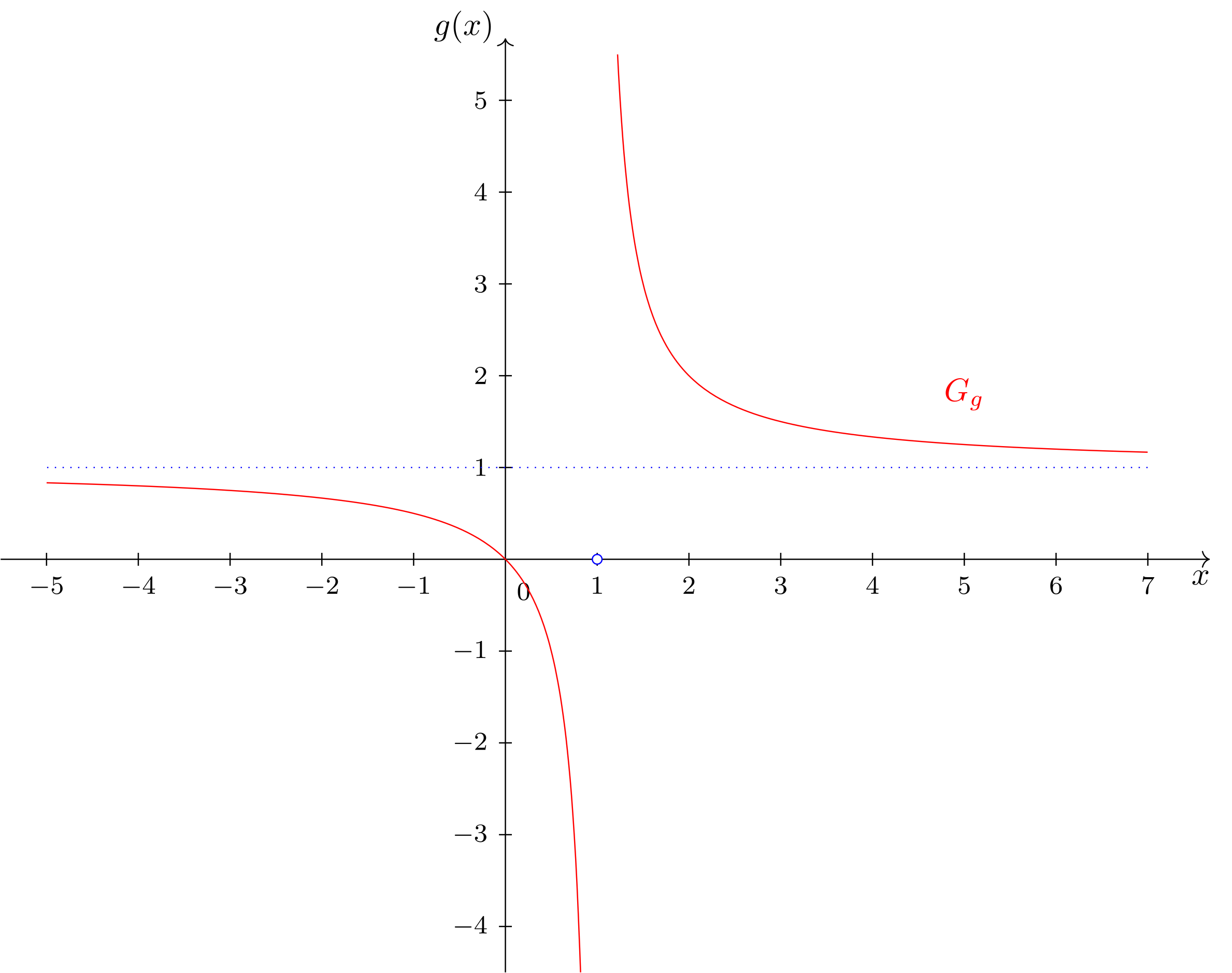
Neben der Polstelle und Definitionslücke bei $x=1$ erkennen wir, dass der Wert $y=1$ eine besondere Rolle spielt. Dieser wird offenbar von der Funktion $g$ nie angenommen. Für die Wertemenge von $g$ gilt $W_g=ℝ\setminus \{1\}$. Stattdessen nähert sich $g$ für ,,sehr große" und ,,sehr kleine" Werte der Veränderlichen $x$ immer stärker dem Wert $1$ an, ohne diesen jemals für eine reelle Zahl $x$ zu erreichen.

Dies erkennt man in der Abbildungsvorschrift $g(x)=1+\frac{1}{x-1}$ folgendermaßen. Für ,,sehr große" ($5$, $10$, $100$, usw.) oder ,,sehr kleine" ($-5$, $-10$, $-100$, usw.) Werte für $x$ nähert sich der gebrochenrationale Anteil $\frac{1}{x-1}$ immer mehr der $0$ an, da $x$ dort im Nenner vorkommt. Tendenziell bleibt also für solche Werte nur noch der polynomielle Anteil $1$ aus der Abbildungsvorschrift übrig. Dieser Anteil kann nun durch eine - in diesem Fall konstante - Funktion beschrieben werden, die als Asymptote $g_{As}$ der Funktion $g$ bezeichnet wird:

${\displaystyle g_{As}:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & ℝ\hfill \\ \hfill x& \hfill ⟼\hfill & 1\hspace{0.5em}.\hfill \end{array}}$
Da es sich in diesem Fall um eine konstante Funktion handelt, wird diese auch als waagrechte Asymptote bezeichnet.