6.2.4 Linear-affine Funktionen
Kombiniert man lineare Funktionen mit konstanten Funktionen, so erhält man die sogenannten linear-affinen Funktionen. Diese ergeben sich als die Summe einer linearen und einer konstanten Funktion. Im allgemeinen Fall, ohne konkret spezifizierte Steigung () und mit einer Konstanten () schreibt man das so:
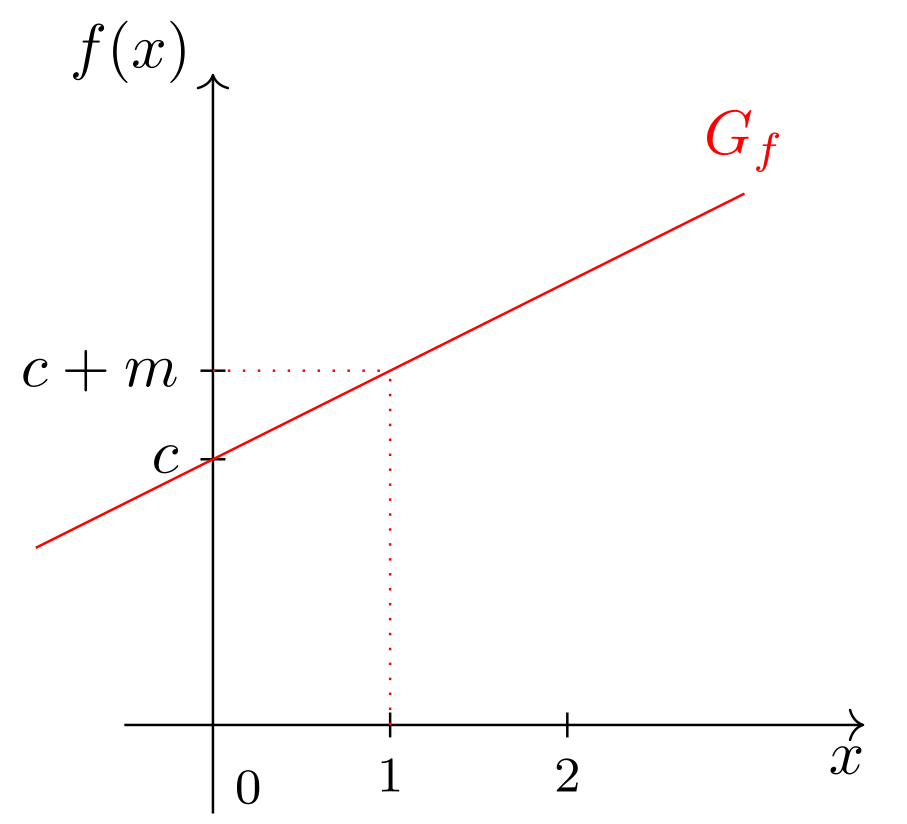
Die Graphen linear-affiner Funktionen werden auch als Geraden bezeichnet. Die Konstante wird für linear-affine Funktionen weiterhin als Steigung bezeichnet, die Konstante als Achsenabschnitt. Der Grund für diese Bezeichnung ist folgender: Betrachtet man den Schnittpunkt des Graphen der linear-affinen Funktion mit der vertikalen Achse, so hat dieser vom Ursprung den Abstand (siehe Abbildung oben). So ergibt sich zum Beispiel für die unten abgebildete linear-affine Funktion
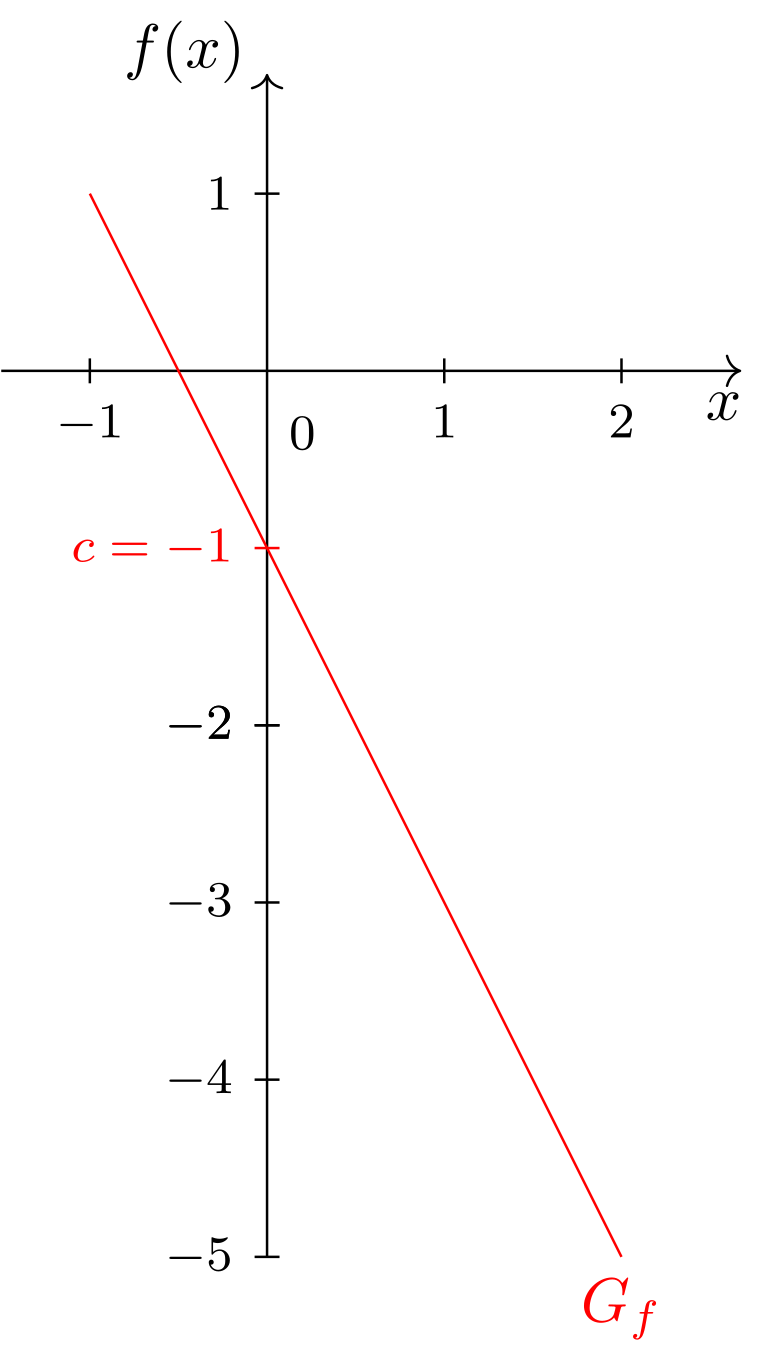
die Steigung und der Achsenabschnitt . Der Achsenabschnitt ergibt sich als Funktionswert bei und somit durch

Abbildung 6.2.10: Skizze (C)
Die Graphen linear-affiner Funktionen werden auch als Geraden bezeichnet. Die Konstante wird für linear-affine Funktionen weiterhin als Steigung bezeichnet, die Konstante als Achsenabschnitt. Der Grund für diese Bezeichnung ist folgender: Betrachtet man den Schnittpunkt des Graphen der linear-affinen Funktion mit der vertikalen Achse, so hat dieser vom Ursprung den Abstand (siehe Abbildung oben). So ergibt sich zum Beispiel für die unten abgebildete linear-affine Funktion

Abbildung 6.2.11: Skizze (C)
die Steigung und der Achsenabschnitt . Der Achsenabschnitt ergibt sich als Funktionswert bei und somit durch
Aufgabe 6.2.4
Was sind die Steigung und der Achsenabschnitt von
Was sind die Steigung und der Achsenabschnitt von
Aufgabe 6.2.5
Welche Funktionen ergeben sich als linear-affine Funktionen mit Steigung und welche mit Achsenabschnitt ?
Welche Funktionen ergeben sich als linear-affine Funktionen mit Steigung und welche mit Achsenabschnitt ?


