2. Geometrie
  3. Winkel und Winkelmessung
  4. Winkel

5.2.2 Winkel

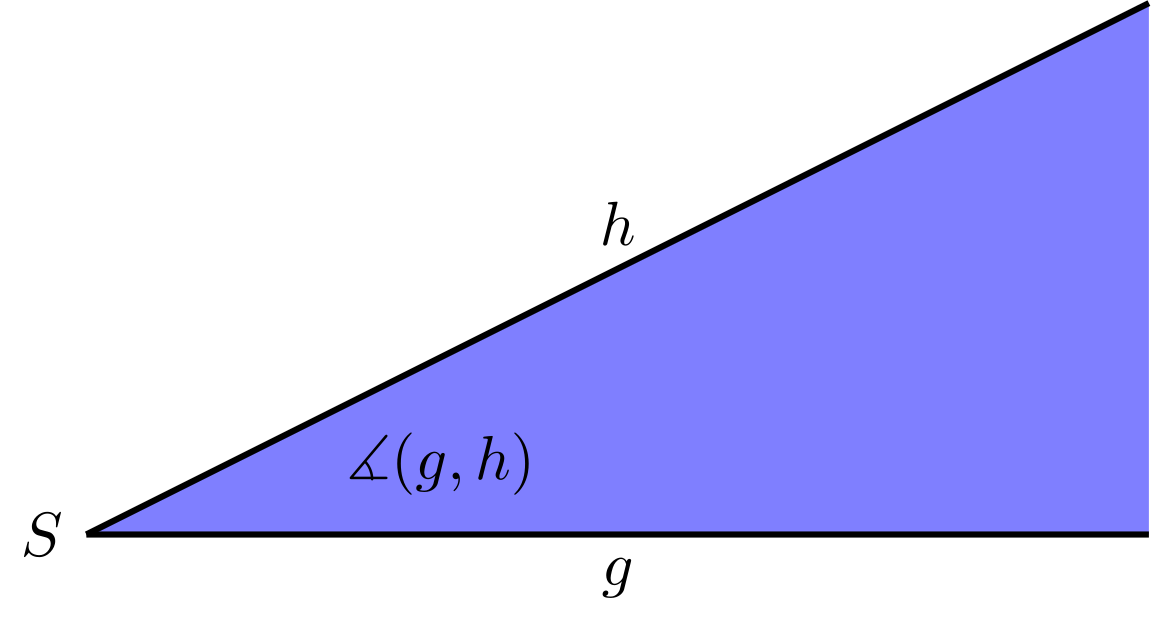
Zwei Strahlen (Halbgeraden) g und h in der Ebene, die von demselben Punkt S ausgehen, schließen einen Winkel ∡(g,h) ein.

./_2FF8AD39_4x.png
Abbildung 5.2.2: Skizze  (C)



Winkel zwischen den Strahlen g und h.


In der Bezeichnung des Winkels ∡(g,h) ist die Reihenfolge wichtig, in der g und h aufgeschrieben werden. ∡(g,h) bezeichnet den oben beschriebenen Winkel, der dadurch festgelegt ist, dass man die Halbgerade g gegen den Uhrzeigersinn zur Halbgeraden h dreht. Mit ∡(h,g) wird der Winkel von h zu g bezeichnet.

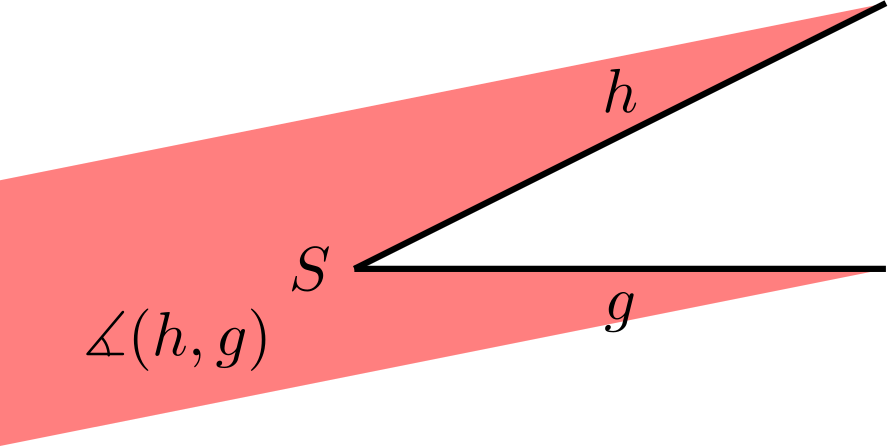
./_891ED568_4x.png
Abbildung 5.2.3: Skizze  (C)



Winkel zwischen den Strahlen h und g.


Der Punkt S heißt Scheitelpunkt des Winkels, und die beiden Halbgeraden, die den Winkel bilden, heißen Schenkel des Winkels. Wenn A ein Punkt auf der Geraden g und B ein Punkt auf der Geraden h ist, so kann man auch ∡(ASB) für ∡(g,h) schreiben. In diesem Sinne werden Winkel zwischen Strecken SA ‾ und SB ‾ beschrieben.

Winkel werden oft mit kleinen griechischen Buchstaben bezeichnet, soweit sie sich vom lateinischen Alphabet unterscheiden, vgl. dazu Tabelle 1.1.8 im Kapitel 1. Indem man Geraden in die Betrachtungen miteinbezieht, lassen sich weitere Winkel entdecken.

Scheitelwinkel und Nebenwinkel 5.2.1  
Es seien g und h zwei Geraden, die sich im Punkt S schneiden.

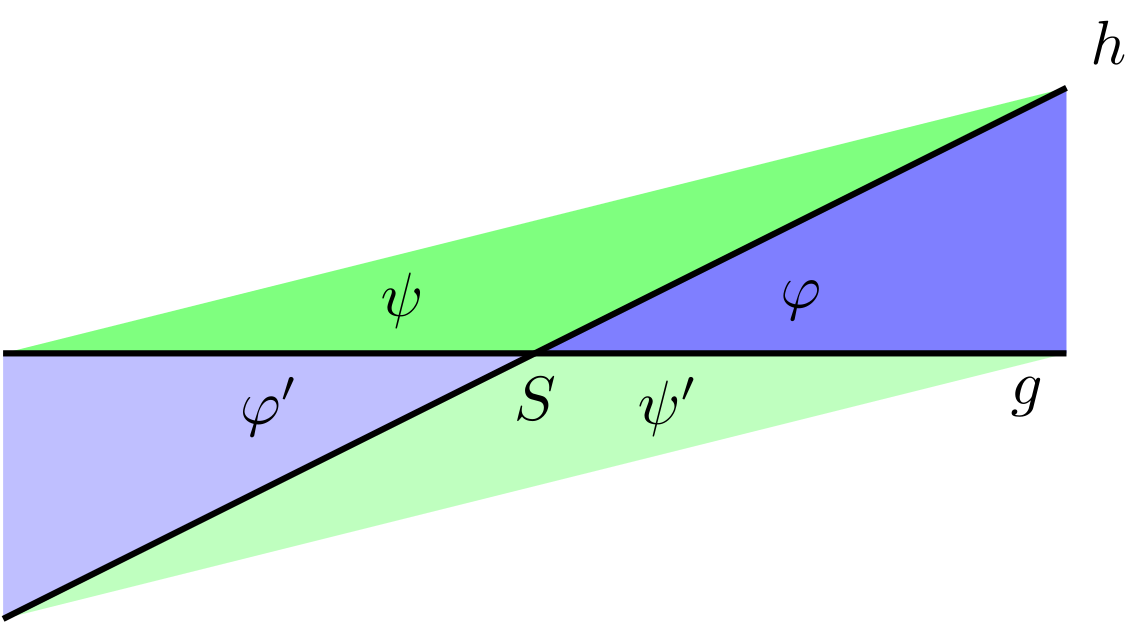
./_2E8A60AC_4x.png
Abbildung 5.2.4: Skizze  (C)



  • Die Winkel φ und φ' heißen Scheitelwinkel zueinander.

  • Die Winkel φ und ψ heißen Nebenwinkel bezüglich g.



In der obigen Zeichnung gibt es noch weitere Scheitelwinkel und Nebenwinkel.

Aufgabe 5.2.2  
Notieren Sie alle Scheitelwinkel und alle Nebenwinkel.



Einige besondere Winkel erhalten eigene Namen. Dabei ist eine Winkelhalbierende w diejenige Halbgerade, deren Punkte von beiden gegebenen Halbgeraden g und h denselben Abstand haben. Dann kann man sagen, dass w den Winkel zwischen g und h halbiert.

Namen besonderer Winkel 5.2.3  
Seien g und h Halbgeraden mit dem Scheitelpunkt S.
  • Der Winkel, der die gesamte Ebene überdeckt, heißt Vollwinkel.

  • Wenn g und h eine Gerade bilden, heißt der Winkel zwischen g und h gestreckter Winkel.

  • Der Winkel zwischen zwei Halbgeraden, die einen gestreckten Winkel halbieren, heißt rechter Winkel. Man sagt dann auch, dass g und h senkrecht aufeinander stehen oder dass g und h orthogonal zueinander sind.



Als Nächstes sollen nun drei verschiedene Geraden betrachtet werden, von denen zwei parallel sind, wohingegen die dritte nicht parallel zu diesen beiden ist. Es ergeben sich dann acht Schnittwinkel. Je vier dieser Winkel sind gleich groß.

Winkel an parallelen Geraden 5.2.4  
Gegeben sind zwei parallele Geraden g und h, die von einer Geraden j geschnitten werden.

./_477F05FB_4x.png
Abbildung 5.2.5: Skizze  (C)

./_74C269C5_4x.png
Abbildung 5.2.6: Skizze  (C)



  • Dann heißt der Winkel α' ein Stufenwinkel zu α, und

  • der Winkel β' ein Wechselwinkel zu β.

Da g und h parallel sind, sind die Winkel α und α' gleich groß. Ebenso sind β und β' gleich groß.


Aufgabe 5.2.5  
In der Zeichnung werden zwei parallele Geraden g und h dargestellt, die von einer weiteren Geraden j geschnitten werden. Erläutern Sie, welche Winkel gleich groß sind und welche Winkel Stufenwinkel beziehungsweise Wechselwinkel zueinander sind.

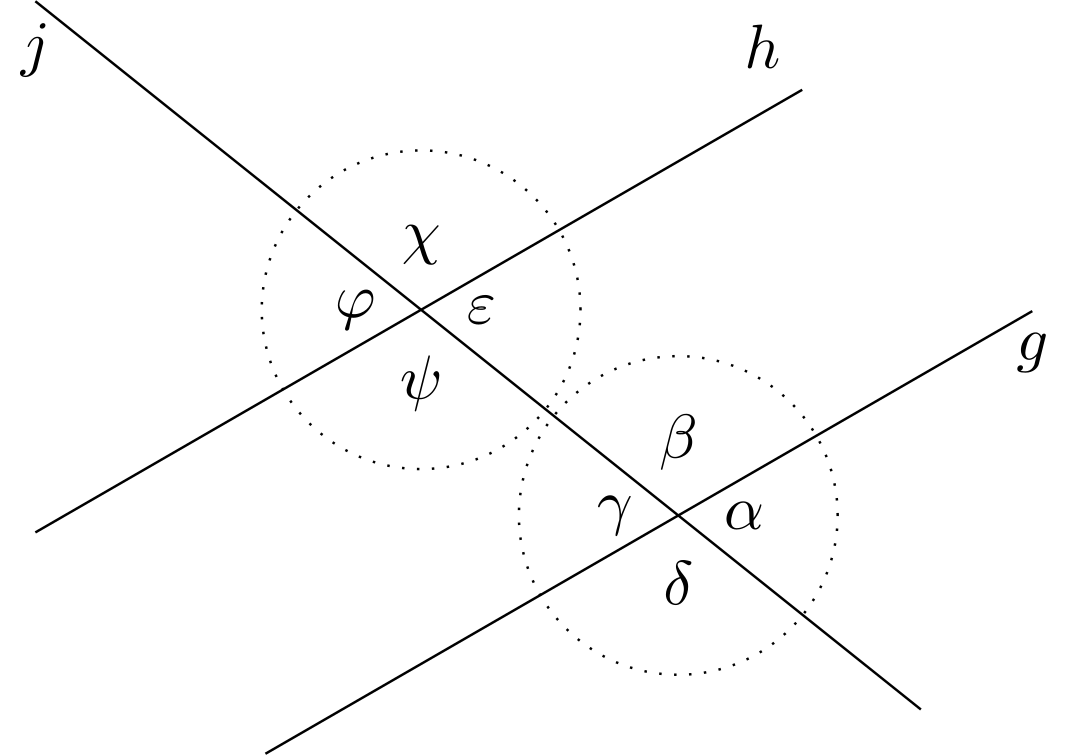
./_9355FC6B_4x.png
Abbildung 5.2.7: Skizze  (C)