8.3.4 Aufgaben
Aufgabe 8.3.5
Berechnen Sie den Inhalt der Fläche , die durch den Graphen der Funktion und die -Achse begrenzt wird.
Antwort: .
.
Berechnen Sie den Inhalt der Fläche , die durch den Graphen der Funktion und die -Achse begrenzt wird.
Antwort:
Aufgabe 8.3.6
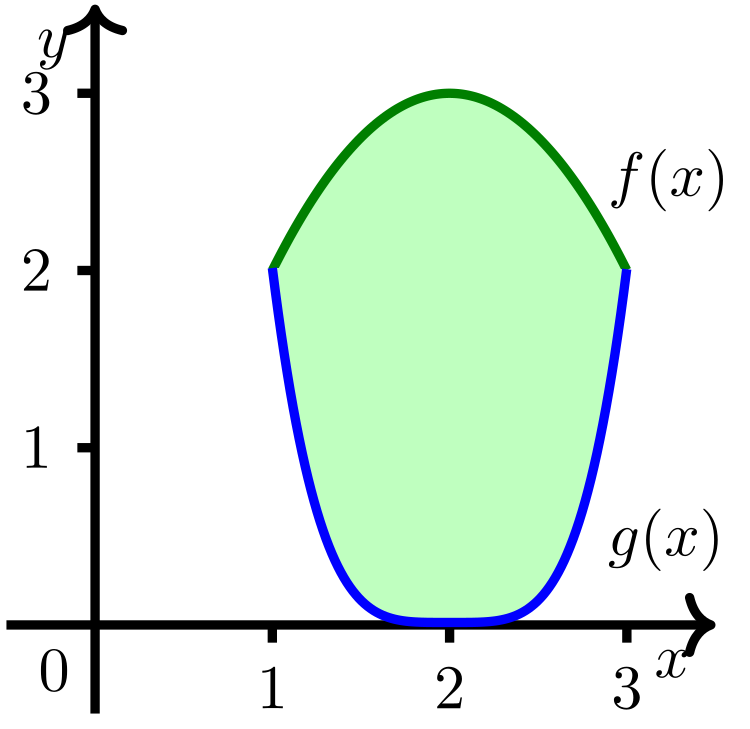
Berechnen Sie den Inhalt der Fläche , die durch die Graphen der Funktionen und eingeschlossen wird. Zeichnen Sie dazu zunächst die Graphen der Funktionen, bevor Sie den Flächeninhalt berechnen.
Antwort: .
.
Berechnen Sie den Inhalt der Fläche , die durch die Graphen der Funktionen und eingeschlossen wird. Zeichnen Sie dazu zunächst die Graphen der Funktionen, bevor Sie den Flächeninhalt berechnen.
Antwort:
In der nächsten Aufgabe wird eine physikalische Fragestellung in der Sprache der Mathematik formuliert, wobei eine Vereinfachung in der Beschreibung vorgenommen wird. Dies soll exemplarisch verdeutlichen, dass die mathematischen Schreibweisen wie hier für Funktionen prinzipiell auch in Anwendungen eingesetzt werden können. In der Praxis werden oft kürze Formulierungen verwendet. So werden beispielsweise Definitionsbereich und Zielbereich einer Funktion nicht explizit notiert, wenn sich diese aus dem Kontext ergeben.
Aufgabe 8.3.7
Berechnen Sie die Arbeit , die nötig ist, um einen kleinen kugelförmigen homogenen Körper , der die Masse hat, gegen die Gravitationskraft von der Oberfläche eines kugelförmigen homogenen Körpers mit Radius und Masse bis zu einer Entfernung zu bewegen (alle Längen beziehen sich auf den Mittelpunkt des Körpers ). Hierbei sind die Masse und die Gravitationskonstante als gegebene Werte anzunehmen, und der kleine Körper wird im Vergleich zum Körper als punktförmig angesehen.
Antwort: .
.
Die Konstanten und müssen in der Lösung stehen bleiben, für kann man gamma eingeben.
Berechnen Sie die Arbeit , die nötig ist, um einen kleinen kugelförmigen homogenen Körper , der die Masse hat, gegen die Gravitationskraft von der Oberfläche eines kugelförmigen homogenen Körpers mit Radius und Masse bis zu einer Entfernung zu bewegen (alle Längen beziehen sich auf den Mittelpunkt des Körpers ). Hierbei sind die Masse und die Gravitationskonstante als gegebene Werte anzunehmen, und der kleine Körper wird im Vergleich zum Körper als punktförmig angesehen.
Antwort:
Die Konstanten und müssen in der Lösung stehen bleiben, für kann man gamma eingeben.