7.1.3 Ableitung
Schreibweisen der Ableitung
7.1.3
In der Mathematik sowie auch in den Natur- und Ingenieurwissenschaften werden verschiedene Schreibweisen der Ableitung äquivalent verwendet:
Diese Schreibweisen haben jeweils die Bedeutung der Ableitung der Funktion an der Stelle .
In der Mathematik sowie auch in den Natur- und Ingenieurwissenschaften werden verschiedene Schreibweisen der Ableitung äquivalent verwendet:
Diese Schreibweisen haben jeweils die Bedeutung der Ableitung der Funktion an der Stelle .
Wenn die Ableitung mithilfe des Differenzenquotienten berechnet werden muss, bietet es sich oft an, den Differenzenquotienten anders aufzuschreiben. Verwendet man die Differenz von und und bezeichnet sie als ,
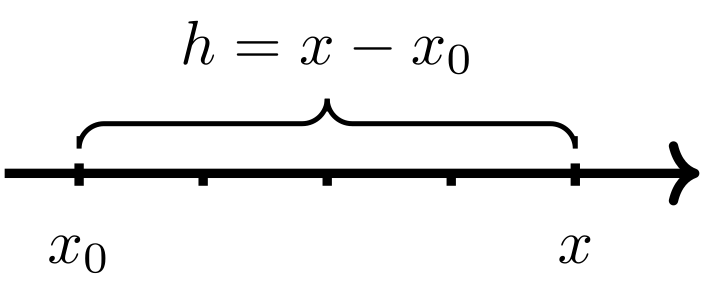
Abbildung 7.1.2: Skizze (C)
kann der Differenzenquotient mit umgeschrieben werden zu
Es wurde keine Voraussetzung darüber getroffen, ob größer oder kleiner als ist. Die Größe kann daher positive oder negative Werte annehmen. Um die Ableitung der Funktion zu bestimmen, muss nun der Grenzwert für berechnet werden:
Wenn dieser Grenzwert für alle Stellen aus dem Definitionsbereich einer Funktion existiert, so nennt man diese Funktion (insgesamt) differenzierbar. Viele der häufig benutzten Funktionen sind differenzierbar. Ein einfaches Beispiel dafür, dass eine Funktion nicht unbedingt differenzierbar ist, ist die Betragsfunktion mit .
Beispiel
7.1.4
Die Betragsfunktion (siehe Modul 6, Abschnitt 6.2.5) ist an der Stelle nicht differenzierbar. Der Differenzenquotient für an der Stelle lautet:
Da größer oder kleiner als sein kann, sind zwei Fälle zu unterscheiden: Im Fall ist , im Fall erhält man . Der Grenzwertprozess, dass sich nähert, führt in den beiden Fällen also auf zwei verschiedene Ergebnisse ( und ). Daher existiert der Grenzwert des Differenzenquotienten an der Stelle nicht. Als Folge davon ist die Betragsfunktion an der Stelle nicht differenzierbar.
Der Verlauf des Graphen ändert seine Richtung im Punkt sprunghaft: Salopp ausgedrückt, weist der Funktionsgraph im Punkt einen Knick auf.
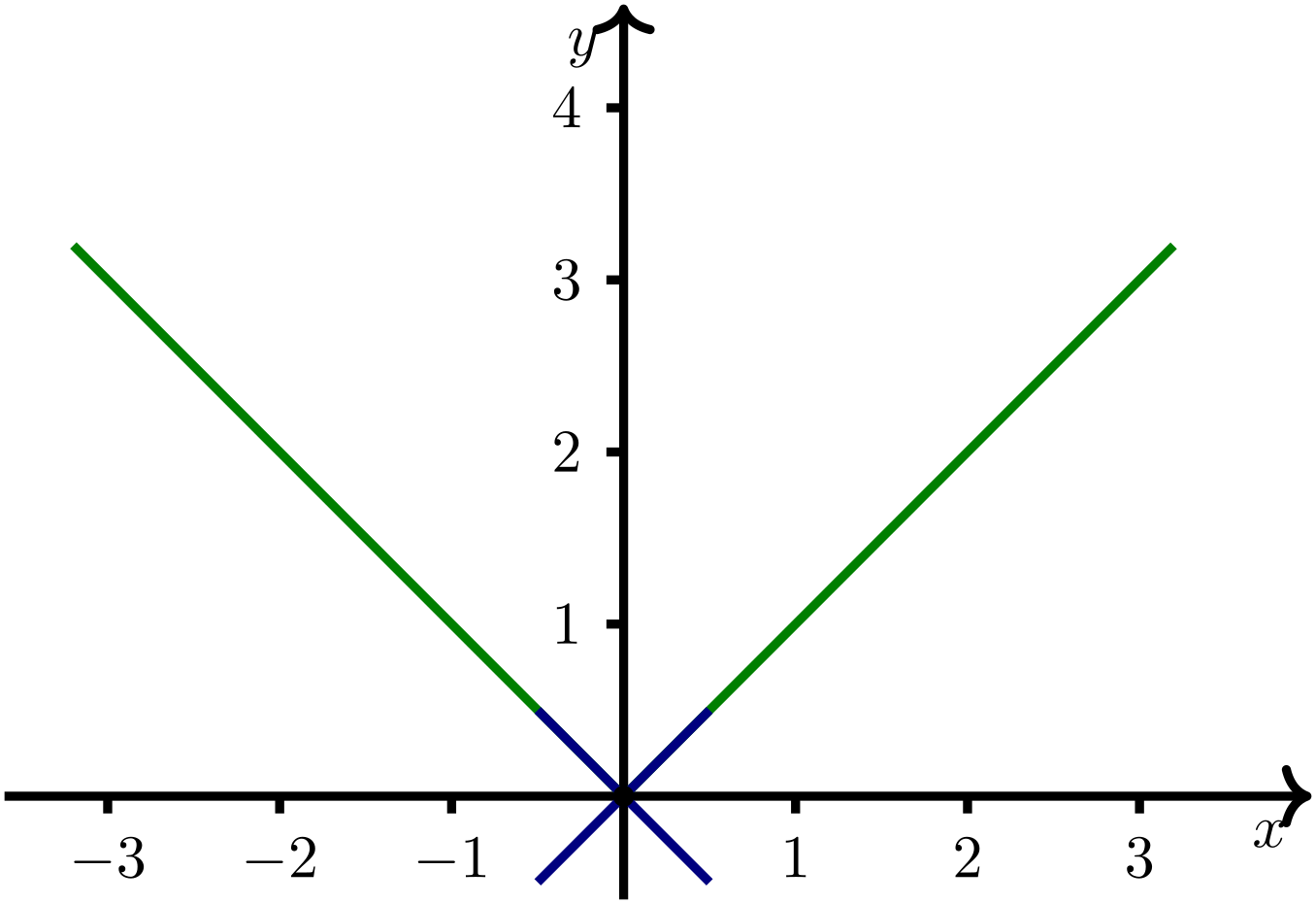
Die Betragsfunktion (siehe Modul 6, Abschnitt 6.2.5) ist an der Stelle nicht differenzierbar. Der Differenzenquotient für an der Stelle lautet:
Da größer oder kleiner als sein kann, sind zwei Fälle zu unterscheiden: Im Fall ist , im Fall erhält man . Der Grenzwertprozess, dass sich nähert, führt in den beiden Fällen also auf zwei verschiedene Ergebnisse ( und ). Daher existiert der Grenzwert des Differenzenquotienten an der Stelle nicht. Als Folge davon ist die Betragsfunktion an der Stelle nicht differenzierbar.
Der Verlauf des Graphen ändert seine Richtung im Punkt sprunghaft: Salopp ausgedrückt, weist der Funktionsgraph im Punkt einen Knick auf.

Abbildung 7.1.3: Skizze (C)
Auch wenn eine Funktion eine Sprungstelle hat, gibt es keine eindeutige Tangente an den Graphen und somit keine Ableitung.


